基于Apriori算法的网络拓扑辨识方法

彭生刚 李吉德

1.平度供电公司 山东 青岛 266700；2长岛供电公司 山东 烟台 265812

0 引言

SCADA系统收集了两类量测数据，一类是遥测量，如有功、无功、电压等；另一类就是遥信量，也就是开关的状态。根据开关量的状态，进行网络拓扑分析后，将结线方式的实际情况反映给调度员。在实时情况下，为调度员提供正确的网络结构是十分重要的，而正确的网络拓扑是建立在正确的开关遥信的基础上的，在实际系统中，遥信抖动和误动时有发生，主要原因有：一次或二次设备本身的原因，各种干扰，远动装置本身或调度端采集处理软件的原因。

现有的软件很多对遥信错误缺少必要的分析，对于网络拓扑结构的分析，更多的是依靠运行人员的经验来判断遥信量的正确与否，这就对于结果的正确性带来很大的不确定性。所以当电网的采集系统中出现开关遥信错误时，而运行人员判断又有误时，将影响到状态估计结果的正确性，可能使得状态估计计算不能收敛，并进一步影响以后的分析（如安全分析，潮流调度等）。而且自从电力市场在各国开展以后，状态估计作为独立系统操作员（ISO）的实时监控工具越来越变得重要。因此一个正确的网络拓扑辨识对于电力系统分析运行产生重要的影响［1-3］。

本文提出了一种新的基于数据挖掘技术的网络拓扑辨识方法，利用SCADA系统所保存的大量历史遥测及遥信数据进行关联挖掘，得到各开关状态的变化与那些量有关，从而根据此关系辨识出正确的开关状态。文章首先对历史数据进行了预处理，然后用挖掘关联规则的方法—Apriori算法对处理的数据挖掘计算，通过设置最小信任度阀值，计算各个开关动作的变化与那些支路潮流的变化及开关变化是强关联的，这样就得到辨识开关状态的规则。

1 数据处理

SCADA系统中所保存的历史数据只是反映每个断面的数据，不能反映每次开关动作所发生的情况，而文章所要辨识的是开关状态的变化。在开关状态没有发生变化，而且负荷也没有发生很大改变的情况下是不需要辨识的，因为我们假定在发生变化的前一时段网络的拓扑状态是正确的。

数据库中所保存的数据形式一般如下：

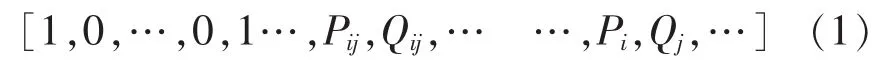
其中1代表开关是合的，0代表是开的，Pij，Qij代表线路的有功及无功。Pi，Qi代表节点的注入有功无功。

对数据库中开关前后发生动作的数据进行整理，形成如式（2）的形式。如果第一个开关发生动作，从合到开，第二个开关从开到合，则前后两个断面的数据如下：从合到开以X表示，从开到合以Y来表示，状态没有变化，则以Z来表示，则（2）式可转化为（3）式的形式，其中共有m个开关。

2 关联规则

关联规则挖掘是数据挖掘的重要研究方向。挖掘关联规则就是从给定的数据集中搜索数据项之间所存在的价值联系。

2.1 关联规则的基本概念

设I＝｛i1，i2，…，im｝为数据项集合，本文主要是Xi、Yi、Zi、｜ΔPij｜等，D为与任务相关的数据集合，也就是SCADA系统所采集到的遥测和遥信量经 （3）式转化后的数据集合。因为最后所需的规则是通过对潮流变化的大小及周围的开关状态来判断此开关的状态， 所以对于｜ΔPij｜、｜ΔQij｜及｜ΔPi｜、｜ΔQi｜设置一个阀值，只有大于此阀值的项，才作为其中的数据项。阀值取多大合适，一是根据网络的结构及负荷水平，二是根据实际运行人员的经验。一个有经验的运行人员通过分析开关发生变化前后支路上的潮流变化以及目前的潮流及开关状态的关系，就可以判断出目前的遥信量正确与否。其中每次开关状态发生变化后所转化的式子 （3）就是一个数据项子集，记为T，即T⊆I。一个关联规则具有如下的形式：A⇒B，其中A⊂I，B⊂I且A∩B＝Φ。如果规则在数据集D中成立，它必需满足最小支持度和最小信任度，只有这样的关联规则才是所需要的强规则。

支持度：在数据集D中有一定比例的数据项T包含A∪B数据项。

信任度：在数据集D中有一定比例的数据项T满足“若包含A就包含B条件”。

具体描述如下：

一个数据项的集合称为项集，一个包含k个数据项的项集称为k项集。一个项集的出现频度就是整个交易数据集D中包含该项集的交易记录数据；这也称之为该项集的支持度。而若一个项集的出现频度大于最小支持度阀值乘以总的数据集D的记录数，那么就称该项集满足最小支持度阀值；而满足最小支持度阀值所对应的记录数就称为最小支持频度。满足最小支持阀值的项集就称为频繁k-项集。所有频繁项集的集合就记为Lk。

挖掘关联规则主要包含以下两个步骤：

步骤一：发现所有频繁项集，根据定义，这些项集的频度至少应等于最小支持频度。

步骤二：根据所获得的频繁项集，产生相应的强关联规则。根据定义这些规则必须满足最小信任度阀值。

2.2 Apriori算法

Apriori算法是挖掘产生关联规则所需频繁项集的基本算法。该算法利用了一个层次顺序搜索的循环方法来完成频繁项集的挖掘工作。这一循环方法就是利用k-项集来产生（k+1）-项集。具体做法就是：首先找出频繁1-项集，记为L1；然后利用L1来挖掘L2，即频繁2-项集；不断如此循环下去直到无法发现更多的频繁k-项集为止。每挖掘一层Lk就需要扫描整个数据库一遍。

在挖掘过程，为了提高按层次搜索并产生相应频繁项集的处理效率，算法用到了下列一个帮助有效缩小频繁项集的搜索空间的性质：一个频繁项集中任一子集也是频繁项集。也即若一个项集I不满足最小支持度阀值s，那么该项集I就不是频繁项集，即P（I）＜s；若增加一个项A到项集中，那么所获得的新项集I∪A在数据集合D所出现的次数也不可能多于原项集I出现的次数，因此I∪A也不可能是频繁的，即P（I∪A）＜s。

2.3 规则的生成

从数据库D中挖掘出所有的频繁集后，就可以较为容易得到所需的关联规则。要产生满足最小支持度和最小信任度的强关联规则，可以利用公式（6）来计算所获关联规则的信任度。

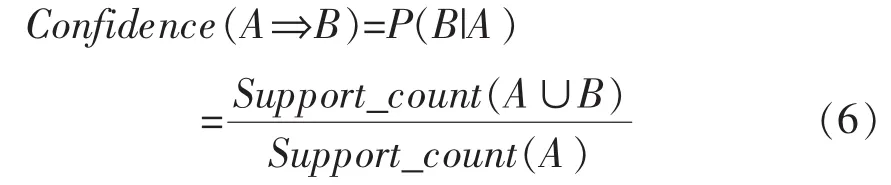
其中，Support_count（A∪B）为包含项集A∪B的记录数目；Support_count（A）为包含项集A的记录数目。

根据电力网络本身的特性，最后网络辨识所需的规则形式如下：

其中i≠j，（7）式所表示的物理意义：通过其它相关开关状态的变化、支路潮流及负荷变化的大小来判断开关状态的变化。通过此规则，根据和此开关状态变化强相关支路潮流的变化及其它开关的状态变化就可以得到所要辨识开关的状态变化，从而可得到正确的开关状态，因为我们假定前一时刻的开关状态已经辨识，是正确的。

最小支持度阀值和最小信任度阀值根据网络自身的特点以及实际的经验来设定。可能一开始，由于缺少实际的运行经验，所定的最小支持度阀值和最小信任度阀值或者太大或过小，从而造成所形成的规则在辨识网络开关状态时产生一定的误差。但随着经验的增加，通过对最小阀值的不断调整，就可以得到能正确判断网络开关状态的关联规则。

3 讨论

1）当网络的负荷水平不一样的时候，开关状态发生变化时，相关支路的潮流变化量也是不一样的，所以在设定｜ΔPij｜、｜ΔQij｜及｜ΔPi｜、｜ΔQi｜的阀值时，不同的负荷水平有不同的阀值。我们按高、中、低三个负荷水平来确定相关的阀值。

2）通过对数据库中的大量数据进行挖掘以后，得到所需的关联规则。然后对所得的关联规则根据负荷水平分别测试，以证明所得的规则是正确可用的。

3）当注入为零或接近于零时，判断不出相关支路开关状态的正确性，因为当开关发生变化时，潮流没有什么变化，但幸运的是零注入时对网络模型及状态估计的结果影响不是很大。

4）当负荷突变和拓扑错误同时发生时，造成辨识的困难。例如当电网的拓扑结构发生变化时，很可能导致节点注入功率的突然变化，切除线路时连锁切负荷，从而导致相关线路潮流发生变化，而此时与相关线路关联的开关遥信又有误，造成辨识的不确定性。但这样的概率比较低，而且当发生切负荷的情况，运行人员会特别注意的。

5）由于网络的结构，线路参数，运行方式等随着时间会不断的变化，这样造成以前的有些规则对于现有的网络状态可能不一定很适用，从而造成网络辨识的错误。只有挖掘的关联规则是反映最新网络状态的规则才是所需要的规则，而最新采集的数据能够反映网络情况。所以对于新采集进来的样本数据，要有一个不断训练的过程，以达到所用的规则是反映最新的网络状态的规则，使得对网络拓扑的辨识达到较高的正确度，供状态估计等所用。

4 结论

本文提出了一种新的基于数据挖掘技术的网络拓扑辨识方法，利用SCADA系统所保存的大量历史遥测及遥信数据进行关联挖掘，得到各开关状态的变化与那些量有关，从而根据此关系辨识出正确的开关状态。文章首先对历史数据进行了预处理，然后用Apriori算法对处理的数据挖掘计算，通过设置最小信任度阀值，计算各个开关动作的变化与那些支路潮流的变化及开关变化是强关联的。随着经验的增加，通过对最小阀值的不断调整，就可以得到能正确判断网络开关状态的关联规则。利用这些规则就可以有效的对网络拓扑关系进行有效的辨识，文章最后利用一个实际配网的应用范例证明了本文方法的有效性。

［1］Yu E K.State Estimation of Power System ［M］.Beijing：Hydraulic and Electric Power Press，1985.

［2］Quintama V，Cutsem T V.Real-time Processing of Transformer Tap Positions［J］.Canadian Electrical Engineering Journal，1987，12（4）： 171-180.

［3］Cutsem T V，Quintana V.Network parameter estimation Using Online Data with Application to Transformer Tap Position Estimation［J］.IEE Proceedings，1988，135： 31-40.