虚拟相控阵超声散射CT成像中的散射面快速定位方法

宋文爱,郭禹姬,杨顺民,陈以方

(1.中北大学软件学院,太原 030051;2.清华大学机械工程学院机械系,北京 100084)

虚拟相控阵超声散射CT成像方法不需要反投影重构,在一定程度上弥补了线性超声CT方法由于线性假设或弱散射假设带来的不足,提高了超声检测的空间分辨率。但是由于该方法需要综合考虑幅值和相位信息,所以需要对虚拟相控阵中的每一个阵元发射、其余阵元(包括发射阵元本身)接收到的所有信号进行处理,信息量较大,从而影响了成像的速度。为了快速而且准确进行超声CT成像,如何快速查找扫描区域(检测区域)内存在的散射源,是提高成像速度和成像质量的关键[1-2]。

笔者提出了一种利用时空压缩的方法,该方法可以快速地识别是否存在散射界面,并能确定散射面产生的信号在时间轴上的粗略位置,为提高CT成像速度奠定了一定的基础。

1 虚拟相控阵超声散射CT成像方法简述

1.1 试验系统方案设计

图1所示的钛合金CSK-IA试块为检测对象,图中标出了试块的尺寸以及阵列传感器的布置区域以及可能引起散射的界面。阵列传感器A具有49个阵元,阵元宽度为 1 mm。传感器频率为6.25 MH z,在被检试块中的波长近似为1 mm。界面1为半径100 mm的圆弧界面,界面 2为深度91 mm的水平界面,界面3为高度6 mm的竖直界面,界面4为深度85 mm,宽度2 mm的水平界面,界面5为高度15 mm的竖直界面,界面6为深度100 mm的水平界面。

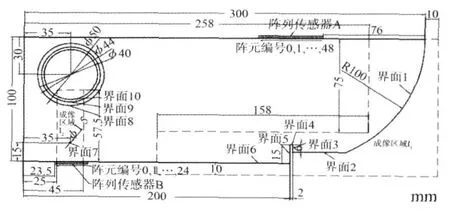
图1 超声散射CT的钛合金CSK-IA试块及探头阵列布设

1.2 虚拟相控阵超声散射CT成像方法

如图2所示,假设目标点P为探测区域内任意一个虚拟扫描点(散射点),有N个阵元的矩形阵列探头,当第i个阵元激励,第j个阵元接收(j=1,2,…,N),可以采集到的N个波列为[3-4]：

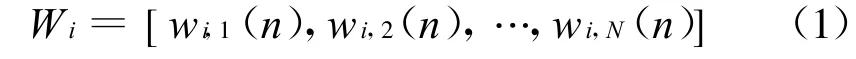
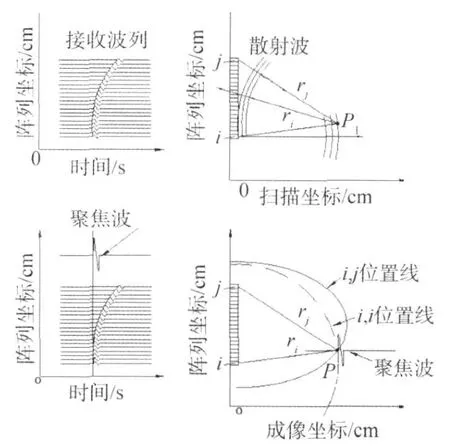
图2 超声散射CT的相位反演成像方法原理示意图

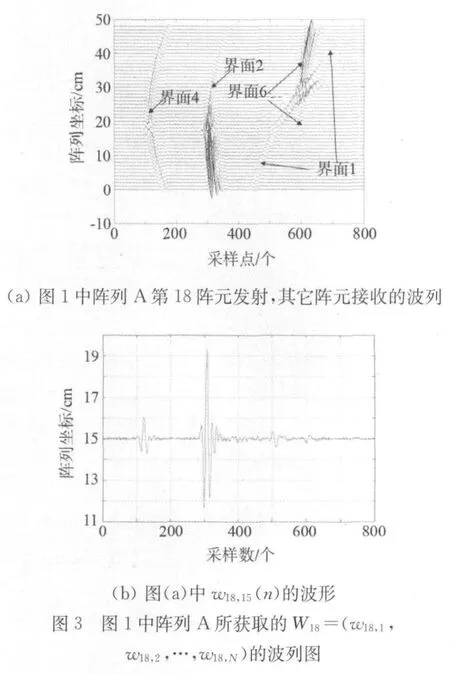
式中W i代表第i个阵元作为发射元时,所获取的时间序列集(波列),W18用波形表示如图3(a)。元素w i,j(n)中i,j=0,1,2,…,N-1;n=0,1,2,…,M-1,代表第i个阵元发射,第j个阵元接收的时间序列信号,M为时间序列的采样点数。w18,15用波形表示如图3(b)。当i=j时为自发自收时间序列。则信号矩阵中的单元wi,j(n)中所包含的空间点P(x,y)声场的超声波信号分量为：

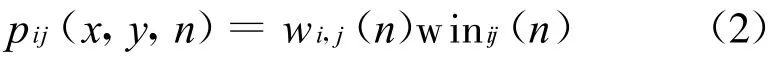
式中w inij(n)为中心为lij,长度为2l的窗口函数。

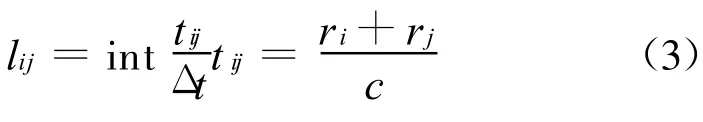
一般l取为：

式中int()为取整函数;c为声速;ri和rj如图2所示,分别为阵元i和j到虚拟扫描点P(x,y)的距离;Δt为时间采样间隔;λ为波长。

窗函数根据具体情况,一般作如下选择：

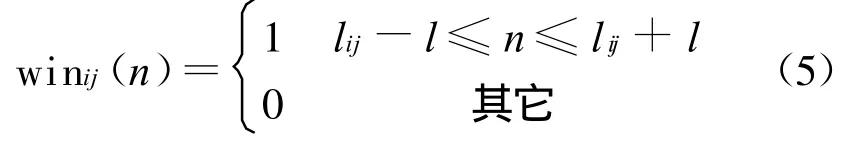
发射阵列在空间一点产生的声场,等于位于这一点的点声源在相同延迟或相移的接收阵列产生的信号总和。则对空间任意虚拟扫描点P(x,y),其声场近似可用下式计算：

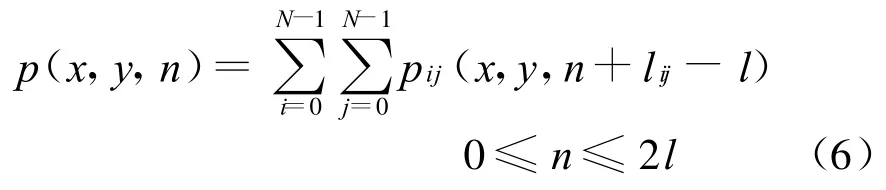
根据需要对式(6)所表示的信号进行处理,取出成像参量,如最大幅值等,形成f(x,y),作为空间点P(x,y)的图像灰度值。对探测区域的每一点(按一定的空间分辨率进行虚拟扫描得到的点)进行上述计算,即可实现对探测区域的相位反演初步成像。

上述方法由于多组信号求和,其统计平均效果消去了噪声,如果目标点没有散射信号到达探头,则合成信号的相对幅值几乎为0。

2 超声波列时、空压缩方法简述

对于有N个阵元的探头阵列,在探测区域内可获得N个如图3(a)所示的波列(时间序列集),每个波列由N个时间序列组成,全部点参与成像运算所需要的时间长,内存需求大,制约了成像速度。如果能实现散射源的快速定位,对于提高成像速度,减少伪像,提高成像质量至关重要[5]。

为了提高成像速度,进行散射源的快速定位[6],首先要将波列的冗余信息进行压缩。

2.1 时间压缩

当检测或扫描区域内存在散射源时,接收信号的幅值增大,在相应的接收阵元上出现局部最大值点。最大值点出现以前的接收序列开始段或反方向最大值点出现以后的结尾段,被认为是冗余信号,可以进行压缩。CT成像时被压缩时间对应的空间点的灰度函数,按没有散射源点接收幅值的均值成像。而扫描区域的大小由阵元大小以及阵元数大小决定。

如图4所示,P为扫描区域内任意散射点,其与起始阵元间的距离为r0,与阵列正中阵元的距离为rN/2,与其距离最小的阵元之间的距离为ry,则与其距离最小阵元的阵元序列号为：

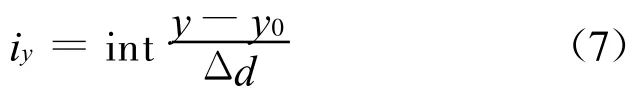
式中y0为起始阵元的坐标;y为与P点距离最小阵元的坐标;Δd为阵元之间的间距。

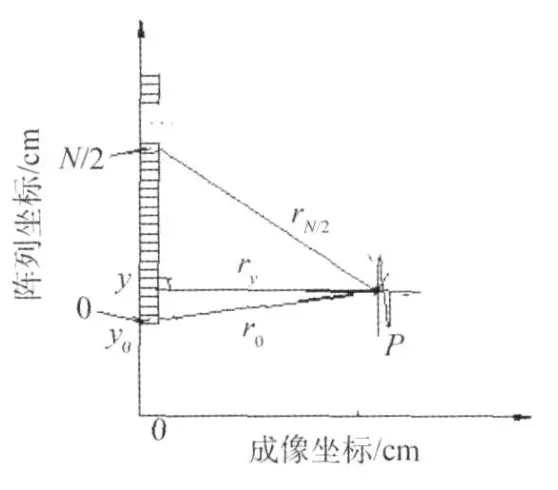
图4 扫描区域内任意散射点P与其距离最近接收阵元关系示意图

设阵列元共有N个,根据式(1),取wi,i(n),n=0,1,2,…,M-1;如果N力偶数,取i=0,N/2;如果N为奇数,取i=0,[(N-1)/2]+1。

对w i,i(n)(n=0,1,2,…,M-1)采用搜索法,寻找出现第一个最大值的时间点l0,lN/2,再根据式(3)可求得r0,r(N/2)。则根据图4,可解得：

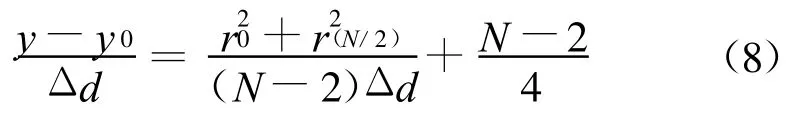
将式(8)代入式(7)可得iy。

对w iyiy(n)(n=0,1,2,…,M-1)采用搜索法寻找出现第一个最大值对应的时间点liy,将得到的时间点左移2l,得：

同理,可以沿时间轴的反方向搜索第一个最大值对应的时间点l01,l(N/2)1,再根据式(7)和(8),求得iy,对wiyiy(n)(n=0,1,2,…,M-1)沿时间轴的反方向,采用搜索法寻找出现第一个最大值对应的时间点l1iy,将得到的时间点右移2l,得：

l的计算方法见式(4)。

由于接收到的散射信号存在一定的相位差,为减小计算误差、时间压缩后不丢失有用的信息,所以nmin和nmax分别向左、向右移动2l。

这样对于所获得的所有波列的时间序列的时间值均压缩到以n=nmin-2l为起点,n=nmax+2l为终点的范围内,并以该范围内的每个时间采样点作为灰度图像的坐标y。

2.2 空间压缩

对如图3(a)所示的波列经过时间压缩后,再进行空间压缩,以采样时间点为坐标x,各阵元的相对起始阵元的位置(对于图1阵列A,从左向右,以第一个阵元为起点,每个阵元的相对位置作为这一阵元所接收信号的坐标)为坐标y,对应的采样信号幅值为灰度值f(x,y)。进行空间压缩后,图3(a)所示的波列转换为二维灰度图,如图5所示。

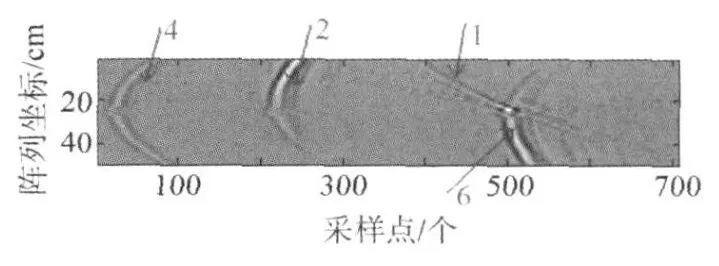
图5 图3(a)所示的波列时、空压缩后的灰度图

由图5可以看出,由散射源形成的散射波前一目了然。

对压缩后的N幅灰度图,分别进一步进行空间压缩,以每一个发射阵元的接收信号为参考信号,进行互相关。即：

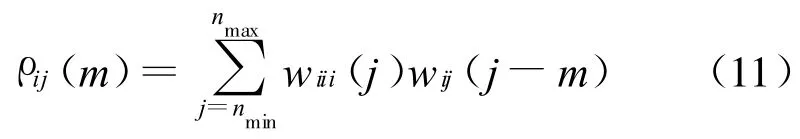
则mj为ρij(m)最大时对应的时间差,将Wi=(w i1(n),w i2(n),…,wiN(n))中的所有w ij(n)(i≠j,n=nmin,…,nmax)平移变为wij(n+mj)。图5平移后如图6所示。

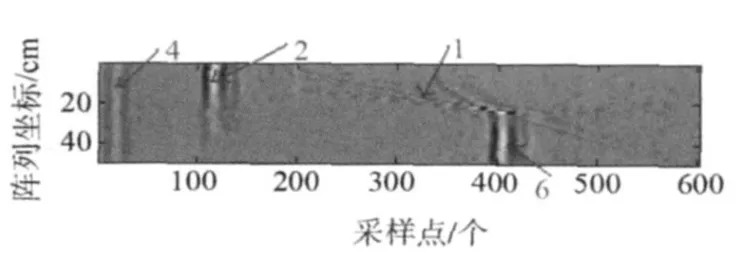
图6 图5进行时间轴平移后的灰度图

将上述移位后的二维信号进一步压缩为时间轴上的一维信号,即：

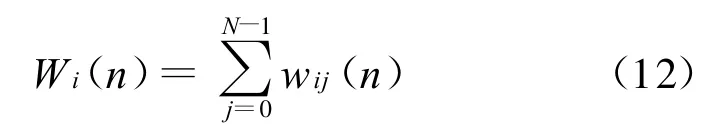
图6所示灰度图移位压缩后的波形见图7。

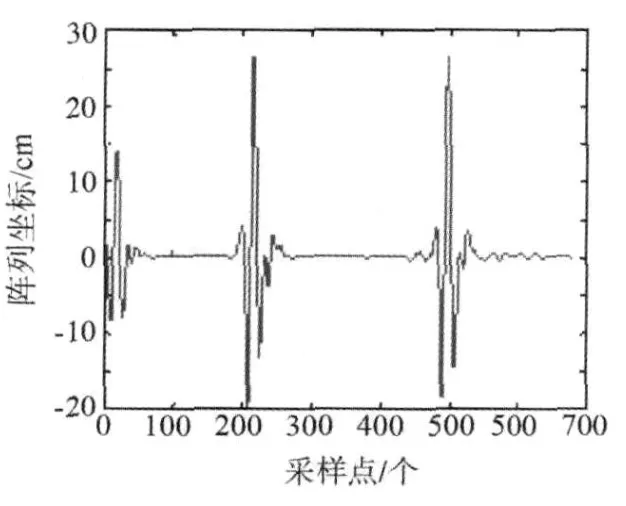
图7 图6压缩的一维信号图

通过对压缩信号的相邻信号值比较求极大,极小值。即：

(1)W i(n)＞Wi(n-1),且Wi(n)＞W i(n+1)时,W i(n)为极大值。

(2)W i(n)＜Wi(n-1),且Wi(n)＜W i(n+1)时,W i(n)为极小值。

依次类推,直到找到最后所需的峰谷值。根据极大值对应的时间轴位置,即可快速准确地找到散射界面的对应位置。

3 试验验证

根据上述快速定位的方法,对图1中界面2、界面4和界面6进行了初步的快速定位,其局部成像如图8所示。

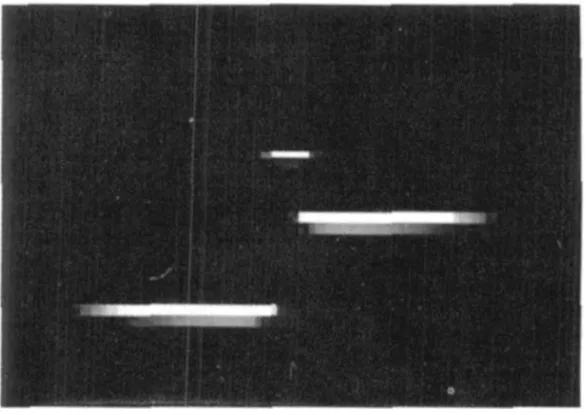
图8 灰度成像

由图8可以看出,初步定位基本符合实际散射面的位置。经过实际计算表明,所确定的散射面为图1所示的界面2、界面4和界面6,误差最大为2mm。

4 结论

提出的利用时空压缩的方法,将虚拟相控阵所得到的超声阵列信号集(波列),变换为位置、时间的二维灰度图,再将其投影到时间轴上。通过研究一维灰度投影的特征,达到快速地识别是否存在散射界面,并确定散射面产生的信号在时间轴上粗略位置的方法可行。通过这种方法可以快速重建材料内部的缺陷断层图像。

[1]倪文磊.超声CT理论与方法综述[J].CT理论与应用研究,2004,13(1)：50-55.

[2]刘波,李朝荣.超声CT成像方法及应用[J].中国仪器仪表,2007(2)：28-31.

[3]Rohde A H,Veidt M,Rose L R F,etal.A computer simulation study of imaging flexural inhomogeneities using p late-w ave diffraction tomography[J].U ltrasonics,2008,48(1)：6-15.

[4]杨奕.超声相控阵检查方法研究[D].北京：清华大学.2003.

[5]彭虎.超声成像算法导论[M].北京：中国科学技术大学出版,2008.

[6]刘超.超声层析成像的理论与实现[D].杭州：浙江大学,2003：6-7.