需求与生产成本扰动下的供应链最优定价订货模型

桂寿平，田飞飞，杨 磊，张智勇

（华南理工大学 经济与贸易学院，广东 广州 510006）

随着经济全球化、产品多样化发展，产品的生产成本和消费者的需求都更加具有不确定性。供应链在运作过程中，可能会遇到各种各样的突发事件，如机器故障、原材料短缺等，使得供应链不能按照预定设想运行。应对这些突发事件有效实时处理方法的理论被称为扰动管理。扰动管理由Jens Clausen、Jesper Hansen、Jesper Larsen和Allan Larsen在2001年的OR/MS Today上提出。随后，该术语被广泛接受并引起了很多学者的关注和讨论。

文献[1-3]分别研究了不同需求函数下供应链的扰动管理问题。文献[4-5]研究了在非线性需求函数和生产成本函数为凸函数的情况下，需求发生扰动时，由一个供应商和一个零售商组成的供应链面临的管理问题。文献[6]分析了一个供应商和一个零售商组成的供应链中，市场需求为市场价格的线性函数时，市场需求和生产成本同时发生扰动情况下，供应商的扰动管理决策。文献[7]分析了一个供应商和一个零售商组成的供应链模型，当市场需求为市场价格的非线性函数，市场需求和生产成本同时发生扰动的供应链动态模型，根据扰动的不同程度将模型分为4种情形并分别求出最优解。文献[8]研究了在生产函数是凸函数情形下，生产费用出现扰动时，如何用扰动管理方法修改原来的计划，使系统能够平稳运行且对生产存储造成的影响最小。

目前大多数学者都是针对供应链单个因素的扰动问题进行研究，虽然文献[7]对市场需求和生产成本两个因素进行了考虑，假设了生产成本是一个关于Q的严格凸函数，但是没有考虑对生产成本造成影响的其他扰动因素。

本文考虑了市场需求和生产成本同时发生扰动的情况，并假定了生产成本是一个两元一次严格凸函数C（Q，t），其中，t代表市场环境下，除了订货量Q以外，其他扰动因素对生产成本的影响，并建立了由一个供应商和一个零售商组成的分布控制型供应链动态模型，提出了不同情况下供应链的定价及订货策略。

一、模型建立与分析

（一）模型描述

本文建立了由一个供应商和一个零售商组成的分布控制型供应链模型，供应商和零售商都是风险中性的，供应商向零售商提供商品。供应商和零售商均为独立的理性经济人，均为自身利益最大化考虑。并假设两者之间构成了Stackel⁃berg博弈模型，供应商为决策领导者，基于对市场的分析，设定产品的批发价格；零售商为跟随者，根据对批发价格的分析确定市场销售价格和订货量。假定供应商生产的商品使用周期很短，因此本文只需考虑单个生产时间段（单期）的供应链问题。此外，本文仅考虑单一产品定价，也不考虑价格随时间变化所产生的变动。

设p为市场零售价格，w为批发价格，D为市场需求规模。本文假定D是一个被精确掌握的数据，市场的实际需求是零售价格的递减函数。市场需求与零售价格p之间存在着非线性函数关系：Q=Dp-k，k为需求对价格的敏感系数。假设产品生产成本是一个两元一次函数C（Q，t）。t＞0，t的变动代表了生产成本由于其他方面因素变动而受到的扰动。假设C（Q，t）关于t是正相关的，t增大的时候，C（Q，t）也增大。比如金融危机、食品危机等带来的供应链扰动，都增大了生产成本。

（二）需求和生产成本确定型情形

由Q=Dp-k可得：p=（D/Q）1/k。供应链总收益可以写成：

由于C（Q，t）是一个严格凸函数，对f1（Q）求二阶导，可证明f1（Q）是一个严格凹函数，对f1（Q）求导，使f1（Q）=0，则必有一个唯一最佳点Q*，在这一点上，能使得供应链总收益最大。供应链最大收益为：

通过上述分析，可以得出结论：当零售商决定订货量Q*，并设定零售价格为p*时，能够使供应链收益最大，但是供应商和零售商都是独立理性人，供应商需要设定一个批发价格来引导零售商订货Q*，并把销售价格设为p*。供应链库存管理理论中的全部单位数量折扣合同AQDP（w1，w2，q0）已经被证明可以用来协调供应链。在全部单位数量折扣策略下，w1＞w2，如果零售商的订货量Q＜q0，则单位产品的批发价格为w1，如果零售商的订货量Q≥q0，批发价格变为w2。

已有研究指出，当供应链是协调的时候，供应商的收益是供应链总收益的映射函数，即生产商的收益可以写成：fS=λfmax（0＜λ＜1）。

定理1：

（三）需求与生产成本同时发生扰动情形

本节讨论当需求和生产成本同时发生扰动情况下，供应链如何定价才能实现总体收益最大化。需求发生扰动指市场规模从D变为D+ΔD，需求函数变为：Q=（D+ΔD）p-k。生产成本发生扰动指生产函数由C（Q，t）变为C（Q，t+Δt）。需求和生产成本的扰动必然会引起市场需求Q变动ΔQ，无论ΔQ＞0还是ΔQ＜0，都必然会带来额外成本。供应链总盈利函数可表示为：

其中，（x）+代表了max{x，0}，δ1，δ2＞0，δ1代表当需求量增多时，为了增加生产量而增加的单位成本；δ2表示当需求量减少时，由于处理多余产品而产生的产品处理单位成本。

引理1：假设f2（Q）的收益最大值点在Qˉ，则当ΔD＞0的时候，Qˉ≥Q*；当ΔD＜0时，Qˉ≤Q*。

定理2：当ΔD＞0时，供应链最优订货量Q2满足以下取值：

最优价格p满足以下取值：

供应链最大收益f满足以下取值：

相应地，当ΔD＜0时，供应链的最优订货量Q满足以下取值：

最优价格p满足以下取值：

供应链最大收益f满足以下取值：

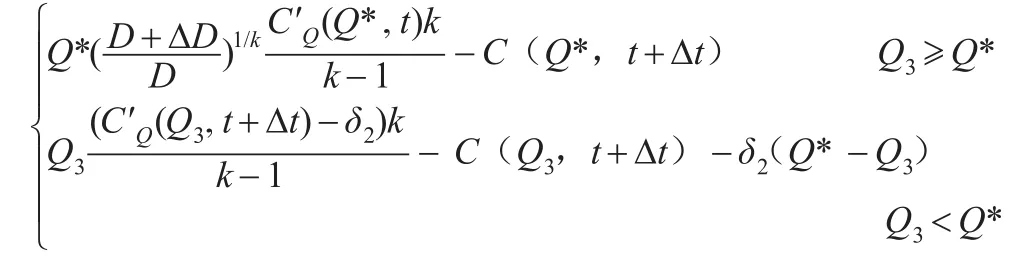
证明：根据引理1，当ΔD＞0时，供应链的总收益函数为：

对Q求导，则可得出最佳订货量满足以下条件：

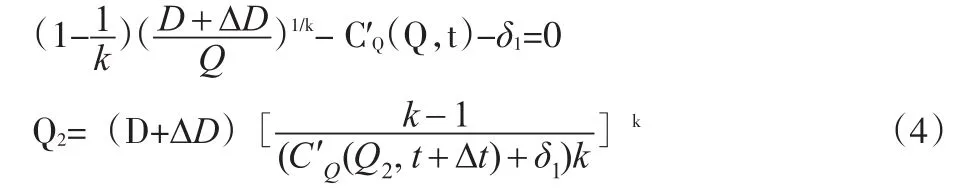
此时，存在着Q2≥Q*和Q2＜Q*两种情况，因为f（Q）是一个凹函数，当Q2≥Q*的时候，f3（Q）的最大值在Q2点，当Q2≤Q*的时候，f3（Q）的最大值在Q*。

在ΔD＞0的条件下，Q满足下列取值：

同理，当ΔD＜0时，供应链总利益函数为：

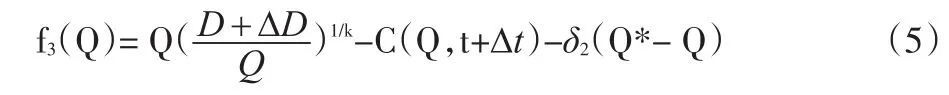
根据上述步骤可分别得出相应的最优订货量、最优价格和供应链最大收益。

由上述结果可知，扰动发生前最优订货量为：

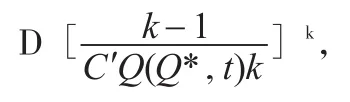
当扰动发生后，订货量和价格都发生变化。本文对各种结果进行分析：

（1）先讨论ΔD＞0的情形，通过比较可得出以下几种情况：①当Q2≥Q*时，假设ΔQ=Q2-Q*，当ΔQ增大时，价格受由规模效应带来的单位成本变动、由于环境等变动Δt造成的单位成本变动和由于需求量增多，为了增加产量而增加的成本变动三个因素影响，供应链的总体利润却不能确定是增大还是减少。零售价格p的大小变化和供应链总利润的大小变化不是同步的，两者的决定条件不同。②当Q2＜Q*时，由于最佳订货量还维持在Q*，但是由于市场需求程度发生了ΔD的变化，因此价格和供应链总体利润也发生了变化，价格变大。由于供应商要调整产量，会带来支出成本的增大，因此供应商的盈利减少，而零售商的盈利却增多。此时，要求供应链中各参与者能够确立新的合作契约，重新分配供应链之间的利润，才能保证供应链能平稳协调的运行下去。

（2）当ΔD＜0时：①当Q3≥Q*时，订货量为Q*。由于ΔD＜0，导致了零售价格p减小，这是和实际运行情况相同的，当市场需求规模减少时，零售商必须要降低价格来增大其销售量。此时，整个供应链的总利润不确定。②当Q3＜Q*时，订货量为Q3。假设ΔQ=Q*-Q3，价格受到由于ΔQ减少造成的单位订货成本变动、由于环境变化Δt造成的单位成本变动和由于需求量减少，处理多余产品而产生的单位处理成本变动三方面的影响。此时，由于生产商要处理多余产品，增加了单位产品支出成本，但是不能确定零售商的收益是否增大，供应链的总体收益同样不能确定。同样要求供应链中各参与者能够建立新的合作契约，重新分配供应链之间的利润，才能保证供应链能平稳协调的运行下去。

（四）两种特殊情况分析

1.生产成本不发生扰动，市场需求发生扰动的情形

生产成本一直为C（Q，t），它只随着Q的变动而变动，t为常数。需求发生扰动是指市场规模从D变为D+ΔD，需求函数变为：Q=（D+ΔD）p-k。在这种情形下，得出定理3。

当ΔD＞0时，供应链的最优订货量Q满足以下取值：

最优价格p满足以下取值：

供应链最大收益f满足以下取值：

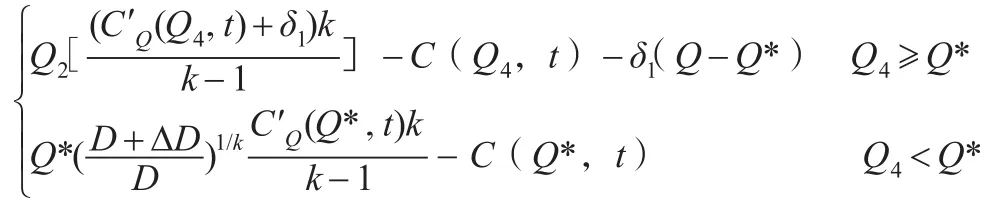
相应地，当ΔD＜0时，供应链的最优订货量Q满足以下取值：

最优价格p满足以下取值：

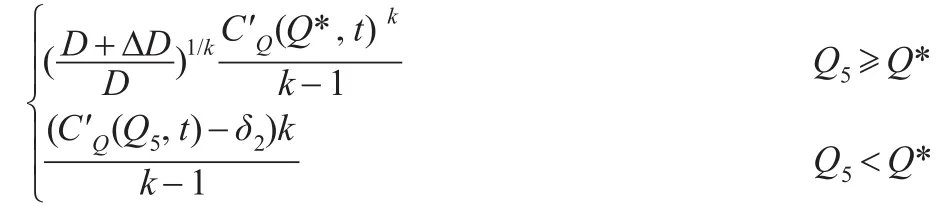
供应链最大收益f满足以下取值：

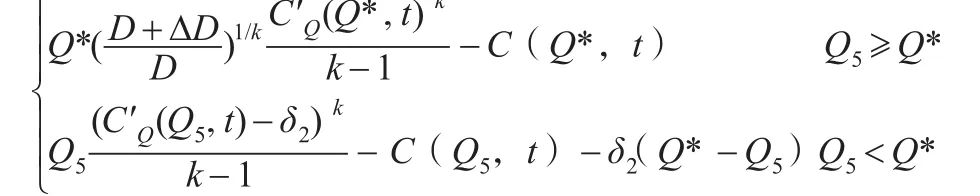
证明过程与定理2证明过程类似，本文省略其证明过程。

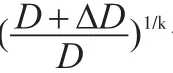
2.需求不发生扰动，生产成本发生扰动的情形

本节讨论当需求不发生扰动而生产成本发生扰动的情形，即市场需求规模保持D不变，生产成本函数由C（Q，t）变化为C（Q，t+Δt）。由于Δt代表除了订货量Q外，其他不利因素对生产成本的影响，所以Δt＞0.此时供应链的收益函数为：

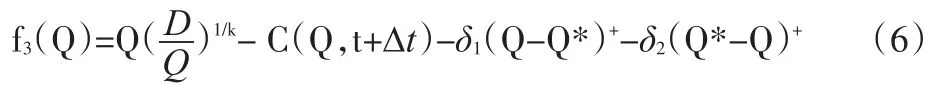
假设f3（Q）的收益最大值点为-Q。模型已经假设C（Q，t）关于t是正相关的。当扰动Δt发生的时候，生产成本相应增大。当-Q＞Q*的时候，供应链收益函数可以简化为：

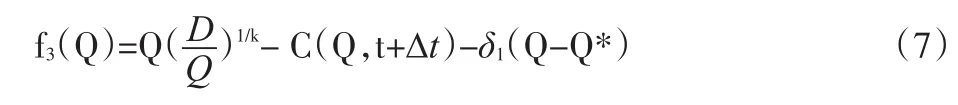
对其求一阶导，使其为0，可得出最优订货量为：

相应的，最优价格和供应链最大收益分别为：

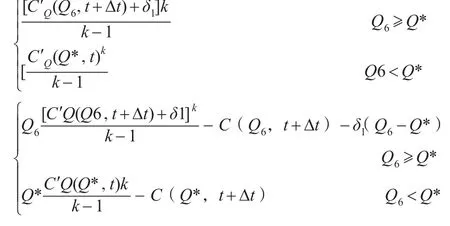
同理，当-Q＜Q*时，最优订货量Q7、最优价格及最大收益分别为:

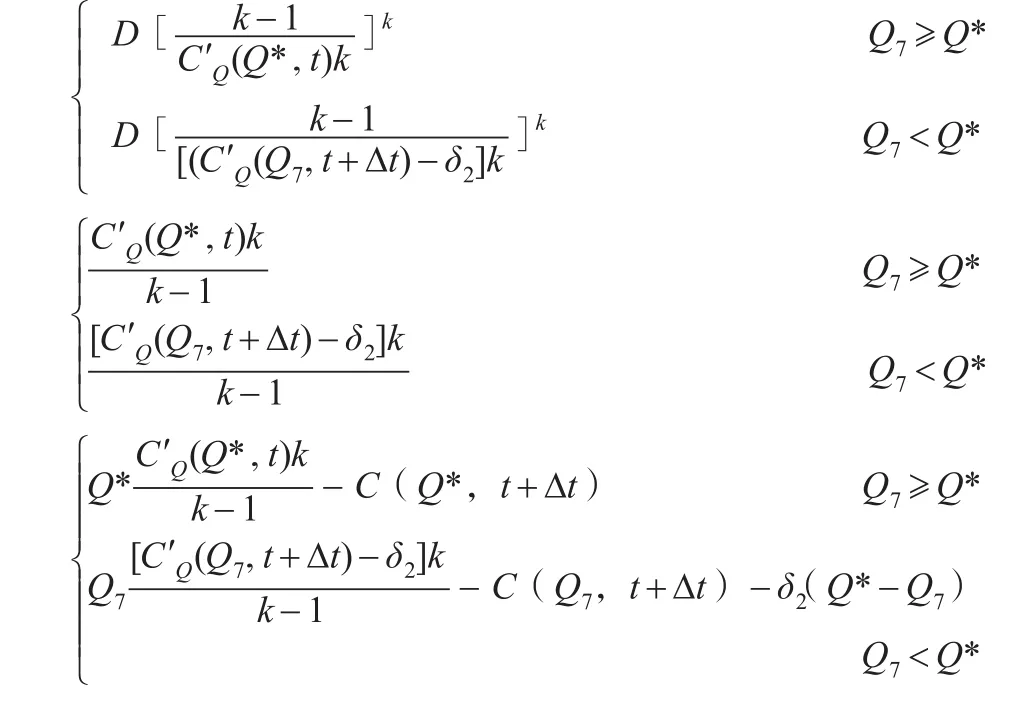
证明过程与定理2证明过程类似，所以本文省略其证明过程。

经上述分析可发现，当生产成本发生扰动时，相应的最优订货量会因Δt的变动而变化。

（1） -Q＞Q*的情形：①当Q6≥Q*时，由于成本增大，最优订货量相比扰动前要变小，但是最优定价会相应提高。由于成本的增大幅度不能确定，所以供应链的总收益不能确定是增大还是减少。供应商的产量降低，需要提高批发价格来增加收益。零售商相应地提高零售价格来增加收益。供应商和零售商需要制定有效的合作契约来协调供应链。②当Q6＜Q*时，订货量保持Q*不变，相应的零售价格也不发生变化，但是由于成本的增大，供应链总收益减少，此时，零售商没有损失，但是供应商的收益降低了，双方需要制定合适的合作契约如收益共享契约来共同承担增加的成本。

（2） -Q＜Q*的情形：①当Q7≥Q*时，订货量保持Q*水平不变，零售价格不发生变化。供应商和零售商同样需要制定合适的合作契约来分担由于由于扰动带来的额外成本。②当Q7＜Q*时，不能确定订货量Q的变动情况，因为此时订货量受到订货量减少引起成本增加、由于外部因素扰动Δt引起的成本增加、处理多余产品而产生的产品处理单位成本δ2三种因素影响。相应的最优价格和供应链总收益也不能确定。

二、数值分析

本节假设单位生产成本函数C（Q，t）=tQ2。假设D=100，k=2，t=0.1，则最优零售价格=3.42，产品需求数量Q*=8.55，供应链的总收益 f1（Q）=Qp-C（Q，t）=8.55×3.42-0.1×8.552=21.93，考虑供应商如何协调整个供应链。如果供应链希望能够得到供应链收益的60%，即λ=0.6.通过定理1，可以得到w2=2.39，很明显，当零售商以批发价2.39获得订货量8.55，并且以零售价3.42卖出，他可以获得8.77的收益，是供应链总收益的40%。

然后，考虑有扰动发生的供应链协调情况。假设△D=40，△t=0.05，δ1=δ2=1.从定理2可得，订货量还是8.55，但是最优价格p*为4.05，供应链的整体收益为23.66。当扰动不明显的时候，零售商保持价格p=3.42不变，销售量Q为7.23，供应链的收益为16.89。

当生产成本不发生扰动，而市场需求发生扰动的时候，最优订货量还是维持在Q*=8.55的水平，最优价格还是4.05，但是供应链的总收益变为27.29.这表明，只有市场需求发生扰动的情形和两者全部扰动的情形相似，但供应链的收益会相应增加。当生产成本发生扰动，而市场需求不发生扰动时，最优订货量与生产成本不发生扰动而市场需求发生扰动的情形相同，供应链总收益降为18.28。

需求与成本同时扰动、分别扰动情形如图1、图2所示。

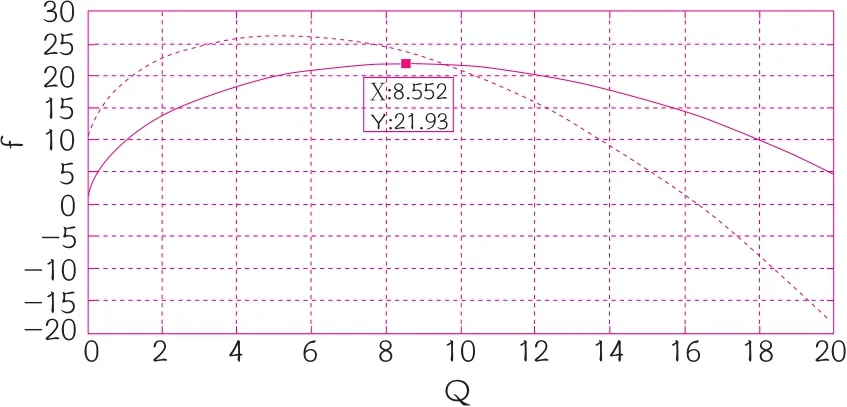
图1 需求与成本同时扰动情形

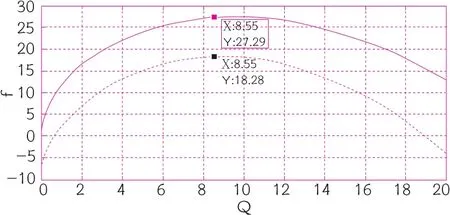
图2 需求与成本分别扰动情形

图1中，实线代表没有扰动发生的情形，虚线代表需求与生产成本同时发生扰动的情形。图2中，实线代表需求发生扰动，生产成本不发生扰动的情形，虚线代表生产成本发生扰动，而需求不发生扰动的情形。这两个图表明，在假定情形下，由于扰动发生，供应链收益反而可能增加，这和前文的分析是一致的。但是，由于扰动发生，零售价格p全部增加，即供应链因为扰动带来的额外成本全部转嫁到消费者身上。虽然供应链的整体收益有增大的可能，但是由于供应商和零售商各自的收益发生了变化，零售商要求分得供应链40%收益的契约将不再适用，因此双方需要重新洽谈，确定新的合作契约等。

三、结 论

本文研究了供应链运作过程中由于突发事件引起的各种扰动问题，构建了包含一个供应商和一个零售商的分布控制型供应链Stackelberg博弈模型。供应商是决策领导者，零售商是追随者。本文假设需求函数为指数函数，而生产成本函数为严格凸的两元一次函数。在此基础上，本文分析了市场需求和生产成本无扰动、市场需求和生产成本同时发生扰动、生产成本不发生扰动，市场需求发生扰动和市场需求不发生扰动，生产成本发生扰动四种情形，分别研究了相应情形下供应链价格、订货量和收益的变动情况，并将发生扰动时得出的结果与没发生扰动的情况进行了比较分析。突发事件下一对多供应链模型的定价订货策略和资源有限条件下供应链订货量及收益分配策略将是今后的研究方向。

[1]于辉.协调供应链如何应对突发事件[J].系统工程理论与实践，2005，25（7）：9-16.

[2]Xu M，Qi X，Yu G，et al.The demand disruption manage⁃ment problem for a supply chain system with nonlinear de⁃mand functions[J].Journal of Systems Science and Systems Engineering，2003，12（1）：82-97.

[3]Huang Ch C，Yu Gang，Wang S，et al.Disruption Manage⁃ment for Supply Chain Coordination with Exponential De⁃mand Function[J].Acta Mathematic Scientia，2006，26B（4）:655-669.

[4]Xu M，Qi X，Yu G，et al.The demand disruption manage⁃ment problem for a supply chain system with nonlinear de⁃mand functions [J].Journal of Systems Science and Sys⁃tems Engineering，2003，12（1）:82-97.

[5]Xu M，Gao X.Supply chain coordination with demand dis⁃ruptions under convex production cost function [J].Wu⁃han UniversityJournal of Natural Science，2005，10（3）:493-498.

[6]雷东，高成修，李建斌.需求和生产成本同时发生扰动时的供应链协调[J].系统工程理论与实践，2006，（9）：51-59.

[7]马骏.需求和生产成本同时发生扰动时的供应链动态模型[J].南京师范大学学报（工程技术版），2007，7（4）：88-92.

[8]Yang J，Qi X，Yu G.Disruption management in production planning[R].Department of Management Science and In⁃formation Systems，McCombs School of Business，The Uni⁃versity of Texas，Austin，TX.78712，2005.