一种基于准同步采样的电网谐波高精度测量方法

刘于祥

(广州南方电力集团科技发展有限公司，广州510245)

0 引言

随着节能技术和自动化技术的推广，如变流设备、变频设备等电力电子装置容量日益扩大，数量日益增多，使电网中的高次谐波愈来愈严重，给电力系统和各类用电设备带来危害，轻则增加能耗，降低电网运行效率，缩短寿命，重则造成用电事故，直接影响安全生产。谐波测量对抑制谐波有着重要的指导作用，研究准确测量电力系统中谐波成分的方法具有重要现实意义。

由于硬件电路输出滞后和电网频率不断波动，采样周期不能与被测信号周期实现严格同步，此时测量结果就将产生同步误差，而基波的每一个微小的同步误差，都将给高次谐波的计算带来很大的误差。

为了减小同步误差，本文提出一种基于准同步采样的离散傅里叶算法，无需采样周期与电网周期严格同步。实验结果表明这种算法对基波和高次谐波参量的测量均能获得较高的准确度。

1 测量原理

准同步采样法是在同步采样法的基础上发展出来的，是一种比同步采样更灵活、更准确、更可靠的采样测量方法。准同步采样最显著的特点是其采样周期不要求与信号周期严格同步，这在实际同步采样难以实现真正同步的场合具有很大的优越性。

准同步采样法的采样周期与电网周期不完全同步，但是非常接近，为减少非同步带来的测量误差，可以在数据处理时通过增加迭代次数来提高测量准确度。

1.1 准同步窗原理

如果不能实现整周期采样，而存在一个采样频率偏差(deviation)Δ

则F1(α)的值为α的函数，并且也是以2π为周期的函数，且

设积分起点为β，则

同样，由于不能严格实现整周期积分

令

经过多次递推后可得到

可以证明

在实际应用中，需要对模拟连续信号采样离散算法处理，上述准同步递推过程可表述如下：

对于式(4)，将宽为n×(2π+Δ)的积分区间［x0，x1+n×(2π+Δ)］等分为n×N段采样得到n×N+1个数据f(xi)，(i=0，1，…，n×N)然后做递推，递推过程见参考文献［2］。

通过多次迭代过程，最终可得到一组权系数ηi，称为准同步算法的权系数，可从数值求积的公式中导出。迭代结果和原始数据关系可用下式表示：

其中

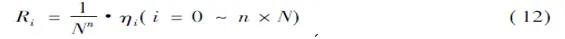
上式为准同步窗函数。

1.2 准同步算法谐波分析

周期信号可表示为三角傅立叶级数或指数傅立叶级数形式。对于任一周期为T的周期信号可表示为：

其中，

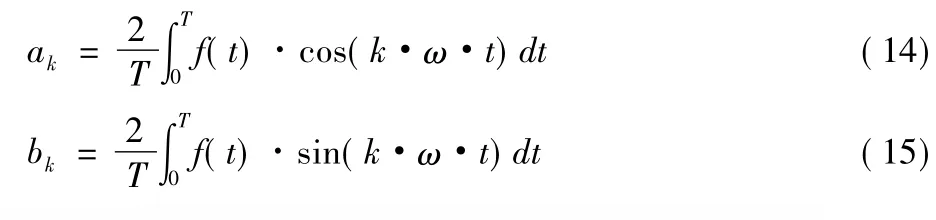
利用准同步算法进行n次推导后得出［1］：

其中，N，k，ηi都为常数，因此，也可用以下表达式：

式中，k=1时，ak和bk分别为信号基波的实部和虚部，k取值2，3，…时;ak和bk为信号k次谐波的实部及虚部。

由上式求得基波及各次谐波的实部和虚部后，可以计算出k次谐波电压、电流有效值和相位：

其中：

各次谐波有功功率及无功功率为：

式(20)中，在确定了采样点数、迭代次数、数值求积方法后，准同步窗的系数是确定的，因此可以事先建立一个准同步窗函数数组。

准同步窗数组的建立：

对每个基波周期采样点数N=64，迭代次数为p=3。选用复化梯形求积公式，所以要采样的点数为pN+1，即193点。则准同步窗函数的计算式为：

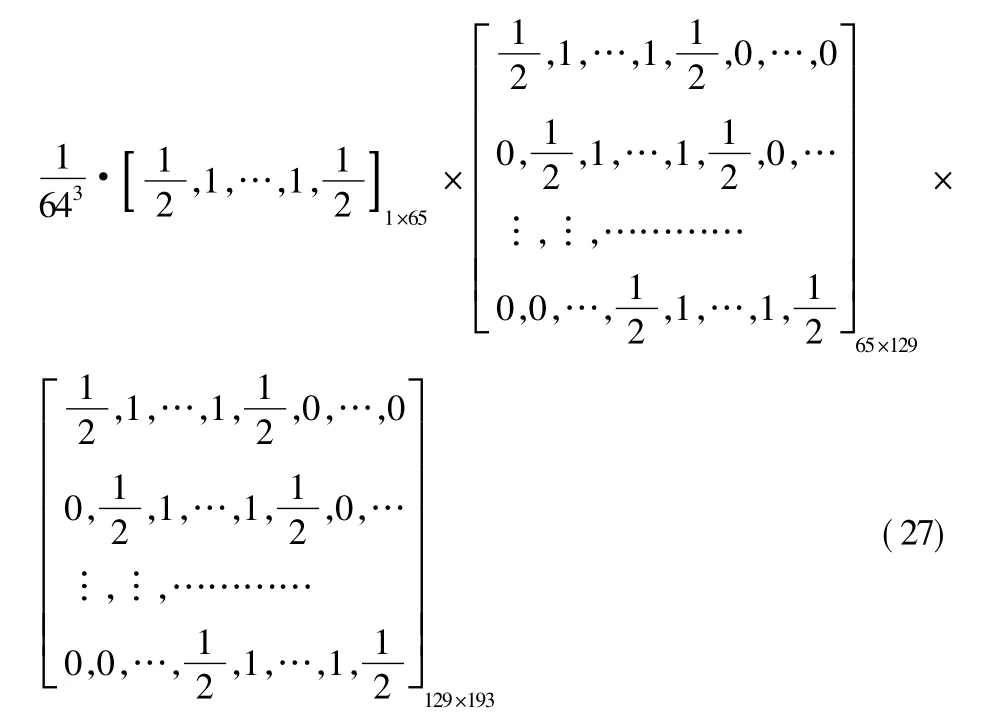
利用准同步窗函数对原始数据进行加权处理，即等效为对数据进行一次同步化处理，从算法实现上也非常简单，只是对原始数据与准同步窗函数数组进行一次乘法的操作。

电网频率波动不会很大，一般均在50±0.5Hz之内，该算法具有较好的测量精度.但在电力频率测量应用中，频率波动在47.5～52.5Hz会经常遇到，采样频率偏移带来的误差将会影响谐波测量精度。可以将频率波动范围分段处理，不同的频率输入选择最为接近的整周期点，然后采用相应的准同步窗函数及正余弦表对数据进行处理，这样准同步算法的谐波测量精度将大大增加。

1.3 算法实现

谐波分析流程图如图1。根据系统计算出的频率来确定本次采样的数据长度，根据当前的周期采样点数选择合适的准同步窗函数(数组)及对应的正余弦表。

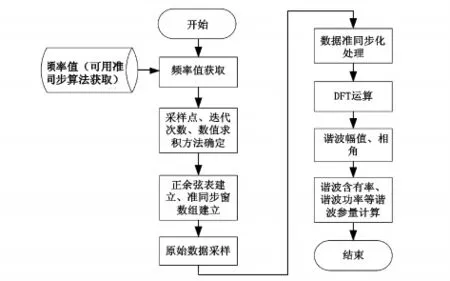
图1 谐波分析流程图

准同步窗函数和正余弦表是一个预先建好的，与采样数据长度等长的数组，它是权系数乘于32768后得到。在本设计中采用复化梯形求积方式，经过三次迭代而计算出相应的权系数。

本文采用在3.2Ksps采样速率下，使用50Hz频率信号对每周期进行采样获得64个点，通常周期采样点数和信号周期不同，但应接近某个整数采样点。在频率偏离50Hz时，本文进行分段处理，自动次选取最靠近的整数采样点。由于采用三次迭代运算，需采样三个周期的原始数据。

原始数据根据采样点数从ATT7022C的寄存器中直接读取，然后进行原始数据准同步化处理，即将原始数据乘以准同步窗数组，变换后的数据经过DFT函数［2］变换，可求的各相电压电流的相角和各次谐波幅值，进而计算出谐波含有率、谐波有功功率和无功功率。

2 硬件电路实现

采用准同步算法，采样周期无需与电网周期同步，硬件电路相对简单如图2。三相电压通过3个电压互感器变化为弱电压信号，三相电流通过3个电流互感器变化为弱电压信号，6路采样信号经过滤波电路后，送入专用计量芯片ATT7022C［3］。ATT7022C具有一个240字节的缓存区，专门用于存储采样数据，支持单、双、三通道同时采样，采样速率为3.2K，本文采用单通道采样，MCU从ATT7022C中读取约3个周波采样数据，按照准同步方法计算出谐波电压、谐波电流、谐波含有率、谐波畸变率、谐波功率等，由MCU输出显示后将计算出的数据通信输出给其他设备。

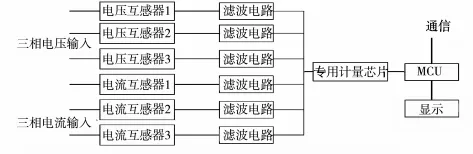
图2 谐波分析硬件原理框图

3 试验结果

选用美国Fluke公司的 FLUKE435电能质量分析仪作为比对仪器，试验结果对比数据如表1。

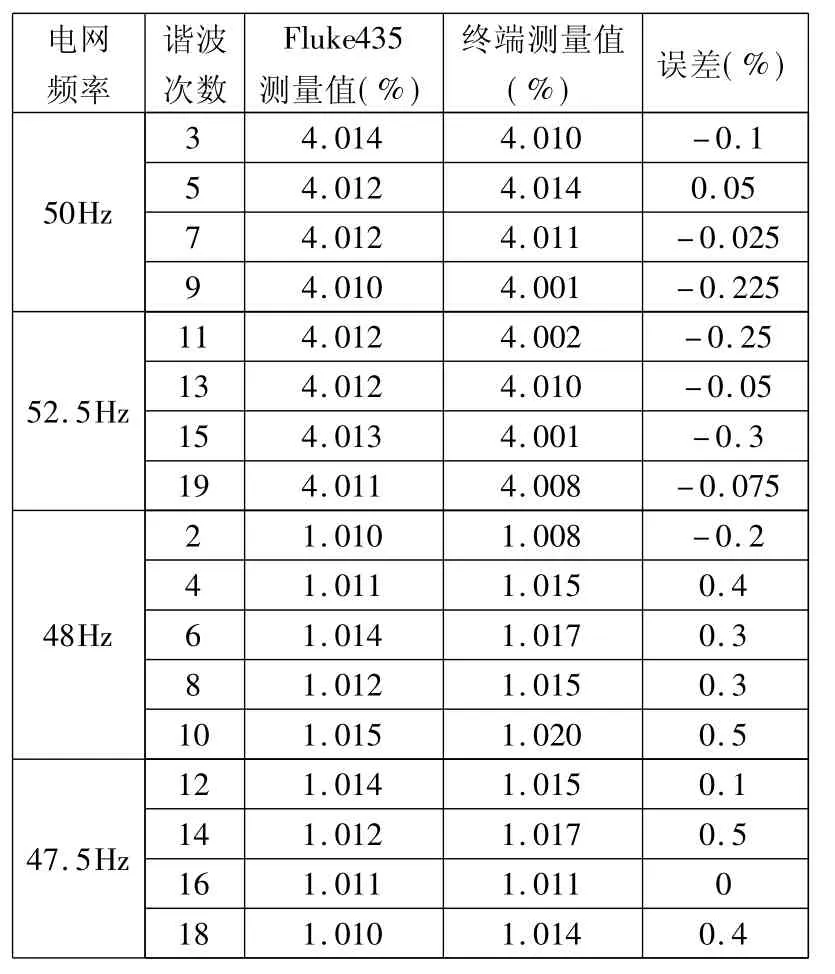
表1 谐波电压测试数据

从测试结果可以看出，在电网频率为47.5～25.5Hz范围内，谐波最大测量误差仅为0.5%，程序运行最长时间约为140ms，足以满足谐波测量的实时性要求，测量精度远远高于GB/T14549-1993对谐波测量仪器的精度要求。

4 结论

本文提出的基于准同步窗的谐波测量方法，利用准同步窗函数对的同步不敏感特性，将原始采样点准同步化，改变其特性使其对同步不敏感，多次迭代使测量精度得到进一步保证。其在一定程度上是牺牲软件开销和内存空间为代价的，但随着电子技术的发展，MCU速度和存储芯片只需较小资源即满足本文软件算法所需要的硬件要求，本文所提出的算法优势就表现得十分明显。本算法无需对信号进行严格的同步采样，降低了硬件复杂度和成本，在宽频率范围均能取得较高测量精度，具有广泛的应用前景。

［1］李芙英，王恒福，葛荣尚.用准同步离散Fourier变换实现高准确度谐波分析［J］.清华大学学报(自然科学版)，1999，39(5)：47-50.

［2］ X.Dai，etal.，“Quasi-synchronous sampling algorithm and its application-Part 2：High accurate spectrum analysis of periodic signal，”Proc.IEEE IMTC193，Irvine，Calif.，May 1993，pp.94-98.

［3］多功能计量芯片ATT7022C用户手册V0.6［Z］.珠海炬力集成电路设计有限公司.2008，2-5.

［4］赵锦成，钱克昌.军用电站谐波测量方法研究［J］.军械工程学院学报，2008，20(5)：48-51.