一种预测水文干旱概率的方法
2011-07-16伊朗阿拉贾尼亚德
[伊朗] S.阿拉贾尼亚德
1 概 述
干旱是指水文循环中的一个或者若干个要素缺水。在某一系统中,在大时间尺度下,如果供水不能满足生物、经济或者社会需水量,干旱就会发生。干旱规划取决于描述旱情并对抗旱具有指导作用的指示因子和触发值。如果干旱指数能为预测干旱开始时间和结束时间提供可靠资料,那么这种干旱指数就是适当的。干旱指数非常重要,但是,在干旱规划中,综合不同的指示因子和触发值预测干旱通常是一个薄弱环节,因为这样的预测常常缺乏操作关联性和科学论证。在干旱规划中提供多个指示因子和触发值会引起问题,原因是目前还缺少综合利用以及评估这些指示因子和触发值的系统方法。基于指示因子如帕尔默干旱程度指数(PDSI)、地表供水指数(SWSI)以及修正的SWSI,采用综合各种水文气候变量的方法解决了这一问题。
SWSI由谢弗和德兹曼(1982年)于20世纪80年代初在科罗拉多州提出,在描述美国西部的可供水量时,该指示因子要优于PDSI。之后,SWSI就成了水文干旱监测中最著名的指数。原始SWSI的基本思想是归一化时使用后验概率。为了改进原始的SWSI,盖伦建议将 SWSI修正为(p-50)/12,式中的p为水库蓄水量 +预测径流的后验概率。即使经过修正之后,SWSI还是存在某些缺陷,难以令人满意地描述某些地区的水文干旱情况。在这些地区,需水量是决定干旱程度的主要要素,而原始的SWSI以及经修正的SWSI在进行干旱程度分类时都没有考虑这一要素。此外,在各种不同的系统中,特别是那些水库蓄水在供水中占据很大比例的系统中,水资源系统的运行在应对水文干旱时发挥了重要作用。当利用多年调节库容满足枯水期的需水量并降低未来干旱的影响时,在干旱识别的过程中考虑调度规程的作用是相当重要的。由于我们对未来情况缺乏足够的了解而导致无法确定诱发干旱的因素时,特别是在进行长期干旱预测的情况下,这一问题显得更加突出。干旱的随机特性是它的特征之一,该特性在干旱监测和预测中都得到广泛关注。
最近,一些研究人员通过组合不同的指示因子对实际干旱进行了适当的监测,克服了传统干旱指数的缺点。拉奥与沃勒尔(1977年)经论证证明,使用包括3个月的降水、月径流量以及PDSI在内的多个指数可以更好地描述旱情。史丹利蒙(2003年)利用多状态马尔可夫模型提出了一种随机方法,该方法可以比较、组合以及选择不同的干旱指示因子。德雷珀和兰德(2004年)提出了一种基于指示因子如可供水及需水量的推算触发值的分析方法,用于优化水库调度中的限水措施。史丹利蒙和卡瓦尔康蒂(2006年)利用系统化方法计算干旱序列,使用的方法包括严重干旱法、一般干旱法、IN触发值和OUT触发值法。与现有方法不同,本文提出了一种分析干旱概率的系统化方法,该方法首先对供与求两种要素的实时监测数据进行可靠性分析,使预测干旱概率所使用的资料更为可靠。
2 提出的方法
本文所提出的预测水文干旱的方法,其基本原理是利用安全因素法进行可靠性分析,其中需水量看作荷载,用D表示,输送水看作阻力,用R表示。当0≤α<1时,发生水文干旱,其中 R/D=α。显然,α值越小,对应的干旱程度就越严重。R和D都是随机变量,可以用概率分布函数表示。对于某一特定的时间段,假定预期可供水量(预测径流 +水库蓄水量)为A,对于干旱强度 α,其发生概率PDrα可用下列公式计算:
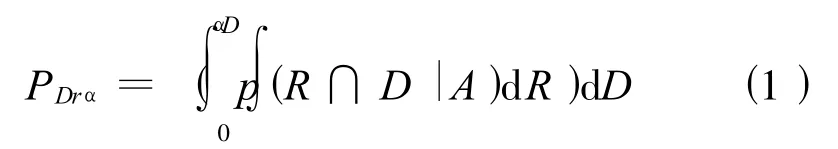
式中p(R∩D|A)为R和D在A条件下的联合概率函数,PDrα为概率分布函数(pdf)下方的面积,也就是关系线R=α D右边的面积(图1)。输送水 R取决于主要因素如预期来水量、需水量、该特定时间段开始时的水库蓄水量以及多年调节库容。此外,由于气候变化影响来水量和水损失,因此,需水量可能变化很大。
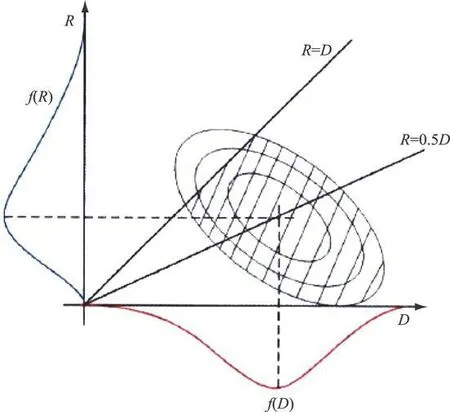
图1 强度为 α的干旱的发生概率
由于A、R、和D之间存在联变,因此,用下列公式计算未来某一时间段内强度为 α的干旱的发生概率:
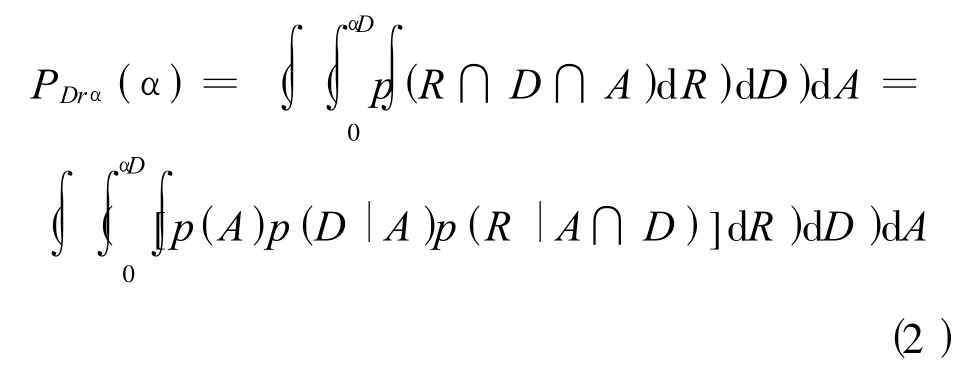
式中p(R∩D∩A)为预测变量R、D和A的联合分布函数,p(A)为可供水量(预测径流 +水库蓄水量)的概率分布函数,p(D|A)为给定预期可供水量条件下需水量的条件概率,p(R|D∩A)为给定需水量以及供水量A条件下输送水的条件概率。
对于本文提出的预测水文干旱概率方法,在统计分析时,可利用不同的统计方法。皮肖塔等(2001年)、阿拉贾尼亚德和波恩(2005年)以及阿拉贾尼亚德等(2006年)提出的统计方法可用来估算未来某一时间段的p(A)。对流域内I和D的历史资料进行统计分析,可计算出p(D|A),其中I为入库径流量。值得一提的是,如果具有区域内需水量变化的资料,那么回归法在分析时帮助很大。帕尔默(1965年)讨论了美国的需水量变化的计算。一些研究人员对需水量驱动的水库调度进行了研究。此外,卡拉莫兹和阿拉贾尼亚德(2007年)还开发出了一个缓解旱情的长期水库调度模型。他们提出的这些方法可以用来建立特定时间段内p(R|A∩D)的分布函数。
3 具体步骤
下面介绍利用该方法进行干旱监测和预测的具体步骤。该方法中的变量和函数,包括了预测某一特定时间段t(假定为一个农业季节)内干旱发生概率所需的所有变量和函数。
(1)确定区域内的径流预测点以及水库。
(2)建立具体预测点与水库之间的下列函数关系:①可供水量为区域内水文气候变量以及水库现有蓄水量的函数,p(A);②需水量是区域内可供水量的函数,p(D|A);③输送水量是可供水和需水量的函数,p(R|A∩D)。
(3)利用公式3计算每一个时间段t起点的A、D及R的联合概率函数。
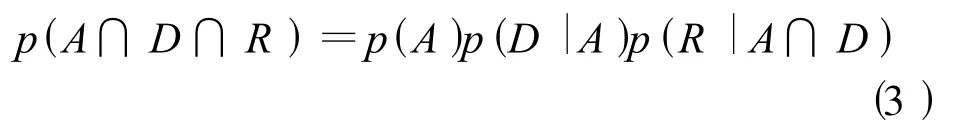
(4)最后,计算p(A∩D∩R)下方的面积,无论α取什么值,R≤α D。
然后,根据PDrα-α曲线确定预期干旱的概率分布函数。图2为使用本文方法监测和预测干旱的算法。
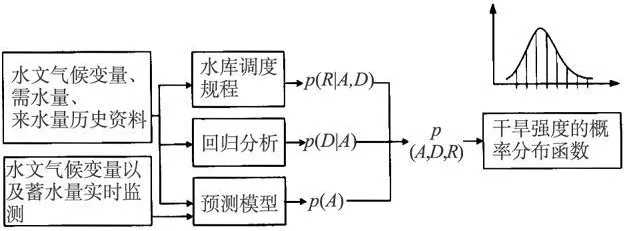
图2 监测及预测干旱概率的建议算法
4 案例研究
本文提出的预测干旱概率的方法在伊朗中部扎延德赫河流域中得到了应用。扎延德赫河的水资源取决于扎延德赫河水库。该流域的水文情势通常用扎延德赫河水库的来水量表示。该水库的年平均来水量大约为16亿m3,均方差为4.25亿m3。阿拉贾尼亚德等人的研究表明,该流域的气候可能受大规模气候信号厄尔尼诺-南方涛动(ENSO)的影响(2006年)。ENSO可以看作是扎延德赫河水库季节来水量和年来水量的一个预测因子。地面水库提供的流域平均年农业需水量为10.88亿m3,均方差为0.73亿m3。同时,流域内年生活用水量和工业用水量为4.16亿m3。干旱时,水库的配水限制仅仅针对农业需水。
如图2算法所示,本文提出的预测干旱的方法需要3个函数:可供水量概率函数(p(A))、已出现径流条件下需水量概率函数(p(D|A))、水库放水量为需水量和可供水量的函数(p(R|D∩A))。下面介绍如何导出本案例的这3个函数。
阿拉贾尼亚德等人(2006年)开发了一个地质统计预测程序(GBPF),利用该程序,根据ENSO信号以及流域水文条件进行长期径流预测。GBPF通过估算方差量化预测不确定度,同时,GBPF可以生成一个预测值考虑多个预测因子的连续正态概率分布函数。在本案例研究中,通过统计分析可知,合理估算流域的年干旱情况,至少需要进行为期3个月的观测(10~12月)。ENSO的著名指数,即南方涛动指数(SOI)、10~12月的实测来水量和降水量被用作水库9个月来水量(1~9月)的预测因子。
扎延德赫河流域农业需水变量与水库来水量呈负相关。图3为扎延德赫河流域1990~2000年水库年来水量与年农业需水量散点关系图。GBPF生成的预测变量为正态分布函数,特定径流量(i)下需水变量的条件概率(p(D|I))也是一个正态分布函数,其均值为 μD|I,均方差为 σD|I,分别用下列公式计算:
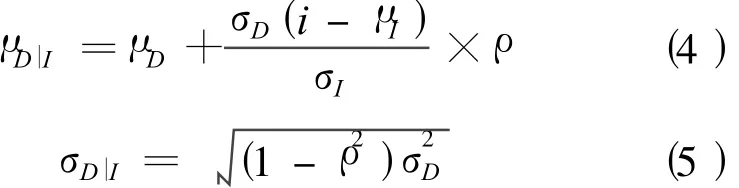
式中 ρ为水库来水量与农业需水量之间的相关系数,μD和 σD分别为农业需水量的均值和均方差,μI和 σI分别为水库预测来水量的均值和均方差,i为预测水库来水量的具体数值。
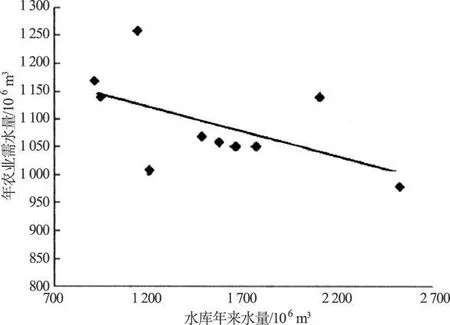
图3 案例中的水库年来水量与年农业需水量散点关系
特定径流量(i)下需水变量的条件概率p(D|I)可以看作可供水条件下需水量的发生概率p(D|A),其中径流预测值中包含了确定性变量,即当前蓄水总量。
根据调度规则可获得地面水库最佳放水量。本案例中的扎延德赫河水库,其限水规则由卡拉莫兹和阿拉贾尼亚德(2007年)制定,干旱时启动对农业需水的限制。利用这一调度规则,根据可供水量的具体数值计算最佳放水量(R)。
5 结果与讨论
以1997年的干旱预测为例介绍本文提出的干旱概率预测方法。正如前面所述,10~12月份的实测预测因子用于预测1~9月份的变量。1~9月份9个月的平均来水量为14.25亿m3。使用GBPF模型估算1997年水库9个月的来水量,其表达式为一个正态分布函数,均值为10.9亿m3,均方差为0.43亿m3。1月份水库蓄水量初始值为4.2亿m3。表1列出了概率值与 α指数的计算步骤。为简便起见,在来水量置信区间范围内将p(I)分为6种类型,每一种类型考虑一个指示因子。同时,以确定性的方式计算输水量R。对于每一个径流量和需水量,可得到一个最佳放水量,同时将其与需水量比较。例如,对于径流量区间10.47~10.9亿m3,期望需水量为一个正态分布函数,其均值为11.348亿m3,均方差为7258万m3,关联的水库来水量指示因子值为10.685亿m3。根据调度规则计算获得最佳关联放水量为10.155亿m3。然后,计算获得的干旱指数0.91即为干旱发生概率(α<1),不发生干旱的概率(α>1)为0.09。应该注意的是,该类型的特定概率约为0.34,在计算干旱发生概率的最终期望值时应该考虑这一数值。使用算法程序,在整个预测来水量和预测需水量区间范围内利用该方法进行计算。最后,对于1997年这一案例,发生干旱的概率为0.72。
表2列出了1997~2002年扎延德赫河流域不同干旱程度干旱的预测结果。如表2所示,预测最严重的干旱发生于2000年,程度最轻的干旱发生于1998年,预测结果与该地区的干旱损失报告高度吻合。不过,本文提出的预测方法的主要优势在于可对系统的可能风险进行分析。
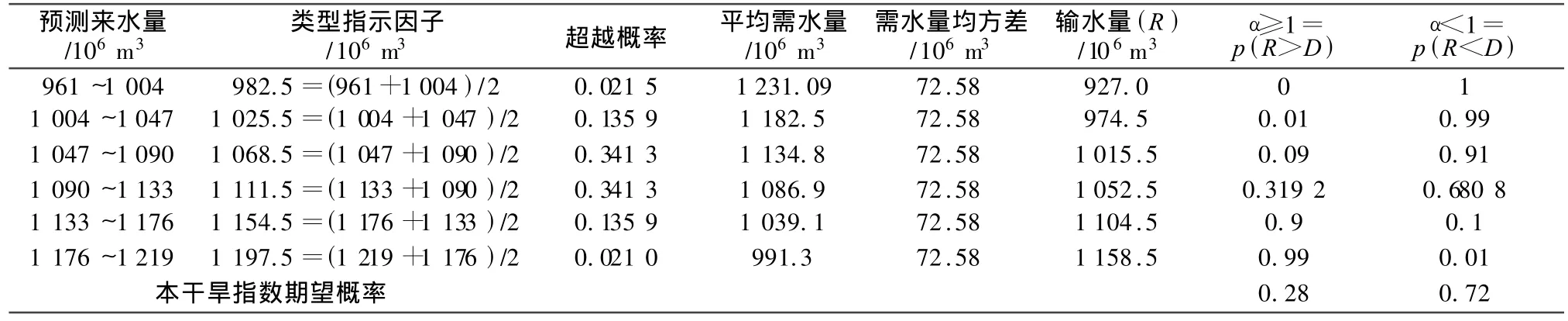
表1 案例干旱预测示例

表2 案例干旱预测结果
6 结 论
提出了一种监测和预测区域干旱的方法,在这些区域中,水库蓄水量在供水和缓解干旱中起重要作用,由于气候变化,需水量变化很大。所提出的方法以概率的方式对需水量和输水量进行可靠性分析并估算某一特定时间段内的干旱发生概率。本文提出的方法旨在尽可能地弥补现有供水程度指数的不足之处。提出的干旱预测程序的主要要素包括水文预报模型、水库调度模型、需水变量函数以及系统的蓄水容量。作为示例,介绍了该方法在伊朗扎延德赫河流域的应用。该方法适用于风险决策,有助于制定限水策略以及目标蓄水容量。该方法对于流域发生干旱时的水资源远景规划的制定具有潜在效用。
