高速公路转向快速路的匝道控制

李 健，贾元华，陈 峰

1)北京交通大学交通运输学院，北京100044;2)乔治亚大学富兰克林理学院，美国雅典城30602

高速公路联络线和城市快速路拥堵可通过适当的匝道控制进行预防与疏导.按受控对象分，匝道控制包括单匝道和多匝道控制，协调控制策略多用于后者.单匝道协调控制指设定多个控制目标，统筹考虑主线状态与匝道约束时的协调控制［1］，其中匝道排队的描述及控制律的优化求解方法值得深入探讨.Yuan L等［2］提出匝道控制中入口流量与排队长度的协调控制问题;Papageorgiou M等［3］提出的ALINEA方法及其后的改进方法［4］多关注控制对主线的影响或方法本身的效率问题.在多目标协调控制方面，主要有考虑了匝道排队、主线通行能力及速度等约束的LP方法［5］和利用Gini系数概念的LP及PID方法［6］等.在智能应用方面，Taylor C 等［7］考虑主线流量、延迟及匝道排队等因素验证了模糊系统 (fuzzy systems，FS)匝道控制的效果;Zhang H M［8］利用神经网络(artificial neural network，ANN)研究了匝道协调控制.在融合算法研究方面，FS与ANN的融合控制较多，主要有Wang F Y等［9］和 Teodorovic D 等［10］的应用研究.与智能算法相比，支持向量机 (support vector machine，SVM)具备解决类似于交通流控制小样本问题的优势，尤其是寻找最优解方面，但对其应用鲜有涉及.此外，由于对实际匝道和主线状态描述不准确，匝道控制研究中控制目标普遍存在信息冗余及缺失等问题.针对以上不足，本研究提出循环等待时间等作为目标参数，应用SVM设计协调控制方法，以深化匝道协调控制研究.

1 匝道排队模型及控制方程

1.1 单匝道模型

图1单匝道模型中，Δ表示路段长度;qup、vup、ρup、qdown、vdown、ρdown、q、v和 ρ分别表示主线上下游断面的流量、速度、密度及路段的平均流量、速度和密度;d和r表示匝道进口流量和入口调节量;Lmax和l表示匝道容量和特定周期内排队长度;l(k)、l(j)、r(k)、r(j)、d(k)和d(j)分别表示第k和j周期的排队长度、匝道调节量和到达量;T为控制周期长度.

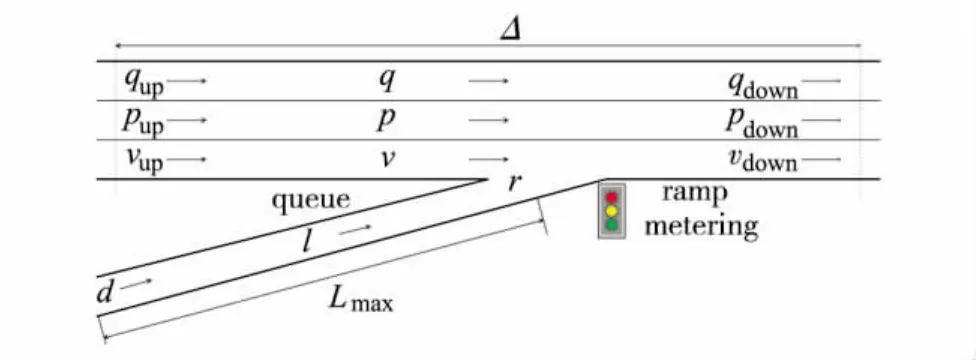
图1 单匝道模型及参数Fig.1 Local ramp model and description parameters

1.2 匝道排队模型的改进

以往对于匝道等待的描述一般采用总体等待时间Tt=l(j)·T，实际上是在每个控制周期开始，就对以往形成的所有单车累积等待时间进行清零后重新计算，这样将造成信息缺失.如在l(j)和d(j)均较小时，将产生总体等待时间基本保持不变而单车累积等待时间持续增加的矛盾，部分车辆进入循环等待状态而无法产生有效的r(j).

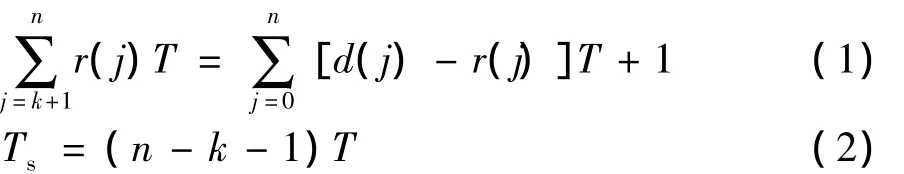
基于排队论思想，建立一种可反映单车累积等待时间的模型Ts.设Ts仅与j=k时的l(k)和j＞k时的r(j)及T有关，与j＞k时的d(j)无关.其中，Tt是基于队列的整体时间;Ts是单车累积等待时间.考虑个体车辆等待的差别，可避免以往整体计算时的信息缺失.本研究后续采用扩展的(Ts－Tt)指标，定义为循环等待时间，以表征匝道排队中是否有车辆出现循环等待现象.

1.3 入口匝道控制目标函数及控制方程

匝道控制在保持区间密度小于最佳密度时，使qdown(k)最大，因此选择主线最大流量作为控制目标.由于区间速度和密度满足一定关系，而行程时间决定于区间速度，因此在选择qdown(k)后，其他可不选择，以避免信息冗余.考虑主线入口匝道对关联道路排队溢出的影响，选择l(k);考虑匝道本身用户真实的公平性，选择(Ts－Tt)，以避免信息缺失.因此，协调控制目标确定为qdown(k)、l(k)及(Ts－ Tt)，交通流模型选择 META［11］.

单匝道多目标协调控制问题可归结为:对于已知时间段主线和匝道交通流状态以及辨识或设定的自由流速度(vf)和最佳密度(ρcr)等参数，满足约束条件，求解控制律r(j)，设定合理的权重Q、S、R使目标函数P最大.

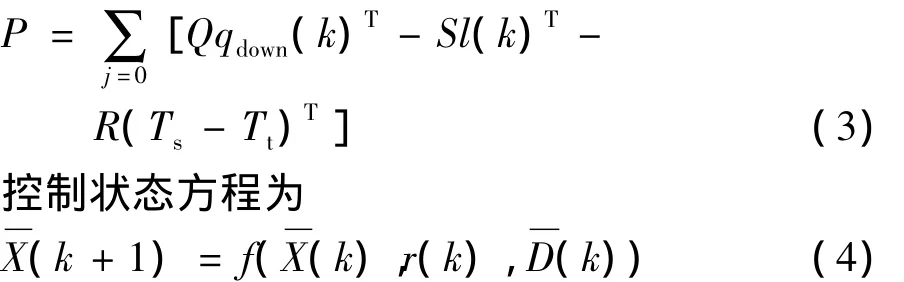
2 SVM机理及控制律方法设计

2.1 SVM基本问题及与ANN机理对比

ANN是依赖于经验的启发式，采用经验风险最小化原则，易导致算法推广不足及陷入局部最小的问题.SVM根据结构风险最小化原则，本质上提高了泛化能力.对非线性问题，可转化为某个高维空间的线性问题，并采用适当的核函数实现分类等，在变换空间中寻求最优分类面，其中只涉及样本间的内积运算，解决了高维计算问题.SVM自由参数更少，相当于线性约束的二次凸规划问题，不存在局部最小问题，局部最优解一定是全局最优解［12-14］.

2.2 RBF为核函数的SVM匝道控制方法设计

非线性情况下分类超平面为wφ(x)+b=0，判别函数为 f(x)=sign［wφ(x)+b］.SVM 在误差项Remp(w)最小的同时最小化置信范围，优化问题为

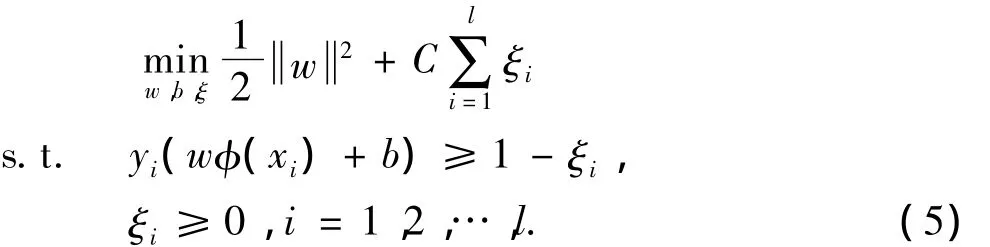
其中，C为惩罚参数，是非线性时引入的非负松弛变量，采用Lagrange乘子法可求解此具有线性约束的二次规划问题.

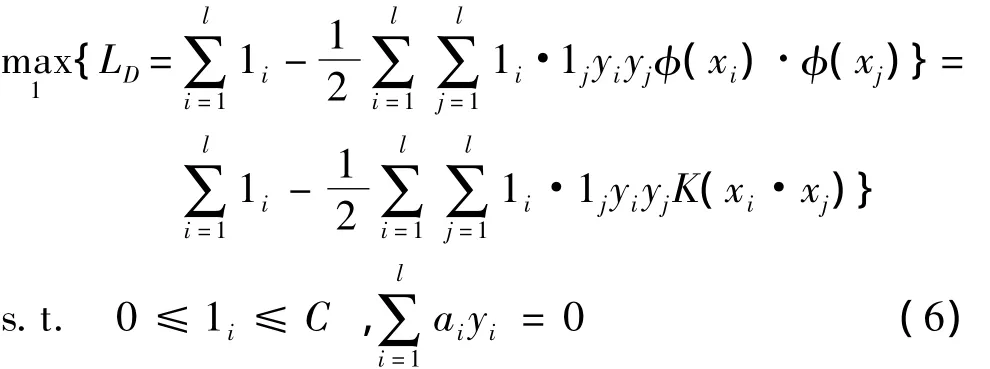
其中，K(xi·xj)= φ(xi)·φ(xj)，是满足Mercer条件的核函数.判别函数，SVM可表达为

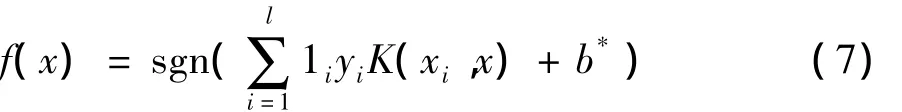
其中，1为Lagrange乘子;sgn()为符号函数;b*为分类阈值.

结合式(5)～(7)，可设计控制律求解方法.

步骤1:对原始交通流数据进行预处理，生成数据集并分组.对交通流数据进行归一化处理得Yi，确定嵌入维数m，构造由ri=xi=(Yi，Yi=1，…，Yi=m－1)与 yi=Yi+m组成的样本点集合

步骤2:考虑径向基函数 (radical based function，RBF)训练效率高以及可任意精度逼近任意连续函数的属性，选择RBF为核函数，确定宽度参数σ，采用动态调整方法对二次规划优化参数C及ξi进行辨识.

步骤3:输入样本集求1及b*，得输出函数

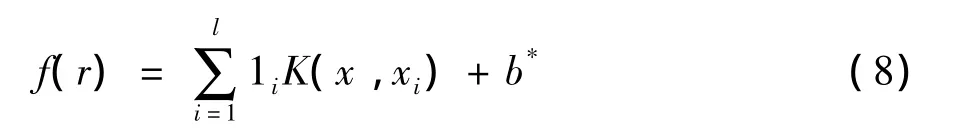
其中，x为待计算匝道调节向量数据r.

步骤4:调节输出计算.根据输出函数计算，设定输出误差区间，超过即返回步骤2调整参数.

步骤5:状态检验.

3 案例仿真与分析

3.1 研究对象

选择G2联络线上行进入北京东四环的匝道为控制研究对象 (如图2)，真实交通流数据由北京城市道路微波检测系统获得，采样周期为2 min.

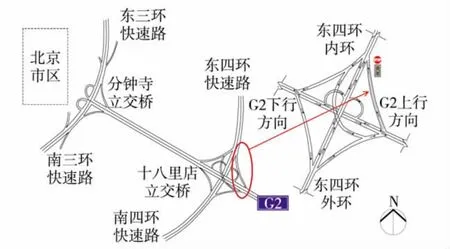
图2 北京东四环匝道示意图Fig.2 Illustration of ramp and mainline

3.2 控制效果对比

无控制时，ρdown在第18个周期附近已达到阻塞密度(ρjam=2ρcr)，随后继续增大;l(k)在第13个周期时超过Lmax，容量溢出;变化最大的是(Ts－Tt)，表明部分车辆等待时间较长，有循环等待现象，如图3(a).ALINEA控制时，r(k+1)=r(k)+KR［Oobj－ Odown(k)］，其中，Oobj和 Odown(k)为期望占有率和下游占有率，仿真中取 Oobj=(1.0～1.4)f(ρcr)，KR=70 ～ 140 pcu/h.由于 ALINEA 输入变量仅考虑d(j)与ρdown关系，易造成上游流量与匝道流量争夺下游空间的情况.在高峰时段开始时，ALINEA可在保证合理ρdown的情况下维持一个较高的r(j)，在第23个控制周期以前，(Ts－Tt)较小，主要是r(j)维持在高平稳区间，循环等待车辆较少，但在ρdown和d(j)持续增加的情况下，由于缺少反馈，输入目标单一，r(j)迅速降低，l(j)则同时迅速增加，很快超过Lmax并溢出.在第25个控制周期以后，由于ρdown和d(j)持续增加，r(j)迅速减小，此时匝道应进入关闭状态，如图3(b).为与RBF-SVM对比，本研究采用RBF-ANN进行控制， 其 输 入 层 为 qup(k)、 qdown(k)、 vup(k)、vdown(k)、ρup(k)和ρdown(k)，输出为r(k)，隐含层数目自动选择，RBF分布密度设为2.0.控制时，ρdown与ALINEA控制下趋势类似，但相对稳定;l(j)在第10个周期开始明显低于ALINEA结果，且在持续高密度条件下l(j)和(Ts－Tt)都有明显降低，图3(c).RBF-SVM控制时，ρdown变化与 ALINEA及RBF-ANN控制相似，但值域总体有所降低;l(j)降低比较明显，在第23个周期后增加速度也明显得到抑制;(Ts－Tt)前期控制较好，且在持续高密度条件下增加速度和快速增加的开始时间方面表现也比较出色，明显优于其他方法，如图3(d).

若调节可有效疏解排队，Ts=Tt;如无法疏解，则部分车辆等待超过一个周期，这时Ts快速增加，Tt增加速率变化不大，匝道排队出现“过饱和”情况，此信息在以往研究中被掩盖，如图4.

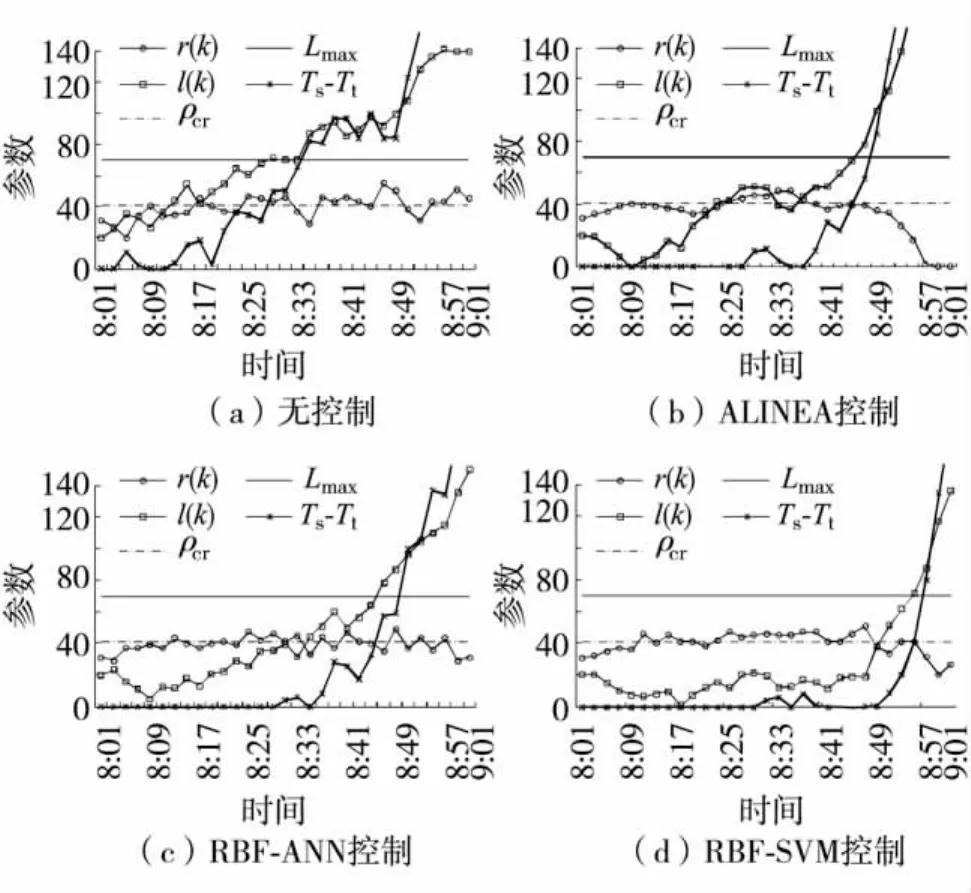
图3 各种控制下匝道参数变化Fig.3 Result profile of ramp under various methods

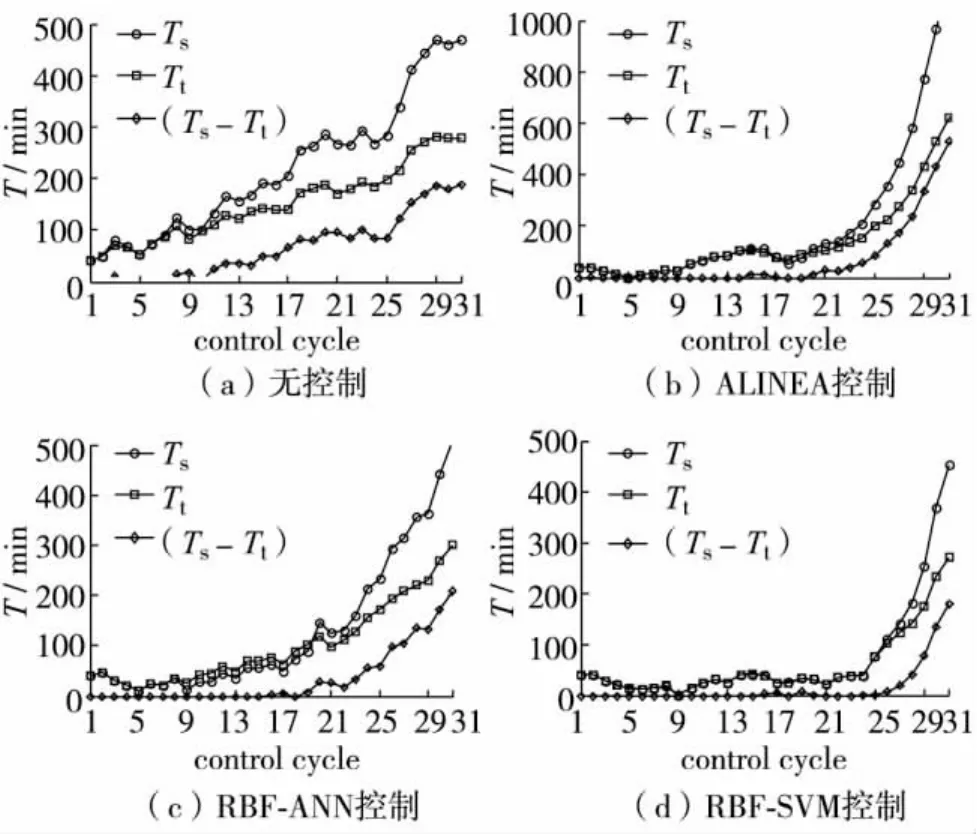
图4 Ts、Tt及 (Ts-Tt)变化Fig.4 Ts，Ttand(Ts-Tt)comparison profile

3.3 仿真分析结论

归纳以上各种控制方法的输出数据如表1.

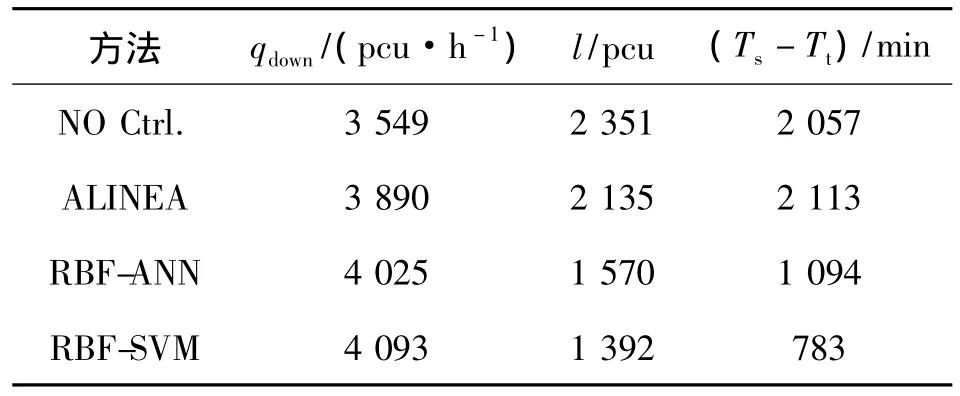
表1 各种控制下的目标值Table 1 Objectives under various methods

设式 (3)中 Q、S、R 分别为0.6、0.2和0.2，对目标值标准化处理后可得折算分值:PNo-Ctrl=71，PALINEA=172，PRBF-ANN=332，PRBF-SVM=439.RBFSVM控制时，qdown分别比No Ctrl、ALINEA及RBFANN增加15.30%、5.22%和1.68%，改进效果并不明显;l分别减少40.4%、34.8%和11.3%，有显著提高;(Ts－Tt)则分别减少61.9%、62.9%和28.4%，效果最为突出.表明RBF-SVM可实现更稳定的调控，有效减少了循环等待时间.

结 语

本研究基于RBF-SVM的匝道控制方法，建立一种新的匝道交通排队模型，提出了更合理的单匝道协调控制参数.根据实地数据仿真验证了该方法的有效性，可准确描述控制前后的交通状态.

［1］Kotsialos A，Papageorgiou M.高速公路网络匝道最优控制效率与公平问题研究［J］.交通研究 (C):新技术版，2004，12:401-420.(英文版)

［2］Yuan L，Kreer J.高速公路匝道控制中排队长度的调整［J］.交通研究 (A):政策应用版，1971，5:127-133.(英文版)

［3］Papageorgiou M，Haj-Salem H，Blosseville JM.ALINEA:一种单匝道反馈控制律方法［J］.交通研究记录:美国运输研究委员会会刊，1991(1320):58-64.(英文版)

［4］Abdel-Aty M，Dhindsa A，Gayah V.高峰期高速公路降低交通事故的几种ALINEA控制策略研究［J］.交通研究 (C):新技术版，2007，15:113-134.(英文版)

［5］杨晓光.考虑进出口匝道排队约束的城市快速道路交通系统动态控制方法［J］.西安公路交通大学学报，1999，19(2):20-26.

［6］张枭雄.高速公路入口匝道控制算法的仿真评价与优化［D］.长春:吉林大学，2005.

［7］Taylor C，Meldrum D，Jacobson L.匝道模糊控制:设计概论与仿真结果［J］.交通研究记录:美国运输研究委员会会刊，1998(1634):10-18.(英文版)

［8］Zhang H M，Ritchie S G，Jayakrishnan R.非线性状态反馈的自适应匝道协调控制［J］.交通研究 (C):新技术版，2001，9:337-352.(英文版)

［9］Wang F Y，Kim H M.基于神经网络的自适应模糊逻辑控制器设计范例［J］.智能与模糊系统学报，1995，1(3):165-180.(英文版)

［10］Teodorovic D，Vukadinovic K.交通控制与规划的模糊集和神经网络方法［M］.波士顿:Kluwer Academic出版社，1998.(英文版)

［11］Papageorgiou M.巴黎Boulevard Peripherique交通流建模及实时控制 (I):建模［J］.交通研究 (A:政策应用版)，1990，5:345-359.(英文版)

［12］罗雪晖，李 霞，张基宏.支持向量机及其应用研究［J］.深圳大学学报理工版，2003，20(3):40-46.

［13］明 仲，林朝哲，蔡树彬.并行PSVM算法及其在入侵检测中的应用［J］.深圳大学学报理工版，2010，27(3):327-333.(英文版)

［14］许伦辉，傅 惠.交通信息智能预测理论与方法［M］.北京:科学出版社，2009.