基于免疫进化的粒子群算法在灌区水资源优化配置中的应用研究

马建琴，魏 蕊，张 鹏

(1.华北水利水电学院，河南 郑州 450011;2.黄河水文勘测设计院，河南郑州 450004;3.河南立新监理咨询有限公司第一分公司，河南郑州 450006)

基于免疫进化的粒子群算法在灌区水资源优化配置中的应用研究

马建琴1，魏 蕊2，张 鹏3

(1.华北水利水电学院，河南 郑州 450011;2.黄河水文勘测设计院，河南郑州 450004;3.河南立新监理咨询有限公司第一分公司，河南郑州 450006)

结合已有水资源优化配置模型，提出了基于免疫进化的粒子群算法，并将该方法应用于濮阳灌区，对其农业水资源进行优化配置.实例计算表明，该混合算法克服了已有算法中初期信息素匮乏，易陷于局部最优解等不足，结果合理，且计算较为简单，可为灌区水资源配置提供理论依据和决策参考.

灌区;水资源;优化配置;免疫进化算法;粒子群算法

灌区水资源系统是一个多水源、多目标、多用户的复杂系统，提高灌区用水效率、实现灌区水资源优化配置能够有效缓解灌区水资源紧缺.解决水资源优化配置问题的关键在于建立适宜的优化配置数学模型，并选择能够兼顾计算精度与计算效率的模型求解方法.粒子群算法［1］作为一种新的并行优化算法，进化初期收敛速度快，运算简单，易于实现，可用于解决大量非线性、不可微等复杂问题的优化，但在进化后期收敛速度明显较慢，易陷入局部极值点［2］.针对以上问题，在灌区总供水量不足的条件下，为保证灌区农作物生产总效益最大.笔者利用免疫进化算法的全局快速收敛性，提出了基于免疫进化的粒子群算法，并应用于灌区农业水资源优化配置问题中.

1 免疫进化粒子群算法及模型求解

1.1 基于免疫进化的粒子群算法

1.1.1 粒子群算法的基本原理

初始化一群随机粒子及每个粒子的位置和速度.每次迭代中，粒子通过跟踪个体极值点(粒子个体本身的最优解)和全局极值点(整个种群目前的最优解)进行更新.设N个粒子中粒子i的信息可用D维向量表示.位置向量为

在每一代进化中，根据速度向量和位置向量的更新方程式更新粒子的位置和飞行速度，并计算各粒子的适应度函数值，进行个体极值点和全局极值点的更新.更新方程式为:

式中:ω 为惯量权重，取值区间为 [0 .4，0.9];c1，c2为加速系数，一般为 2;ran，ran均为区间[0 ，1]上的随机数.在更新过程中，要求设定Vmax限制速度的范围，其每一维一般取相应维的取值范围的10%～20%.

1.1.2 免疫进化算法的基本原理

免疫进化算法的核心在于充分利用最优个体的信息，以最优个体的进化替代群体的进化，通过调整标准差把局部搜索和全局搜索在进化过程中有机地结合起来［3－5］.设N为种群规模，n为种群中个体的编号，d为个体中免疫细胞的编号，则由父代生成子代的公式为

式中:xn(k)为第k代种群中第n个个体;( k )为第k代种群中最优个体编号为d的免疫细胞;，分别为初始种群与第k代种群中第n个个体的标准差;A为标准差动态调整系数;σε为收敛基数;N(0，1)为产生的服从标准正态分布的随机数;K为进化代数.

标准差的动态调整是免疫进化算法的重要技术环节.通过标准差的动态调整，免疫进化算法第1阶段侧重于全局搜索，第2阶段侧重于局部搜索.标准差的调整方式有指数调整法、双曲调整法、混合调整法3种，其中双曲和混合调整法中的标准差变化较平缓，能较好地平衡全局搜索和局部搜索［6］.文中采用混合调整法进行计算，公式为

式中 μ，θ均为参数，且 μ ＞0，θ＞0.

选取我院诊治的周围型肺癌患者40例，回顾性分析其全部的临床资料，其中男22例、女18例，年龄39～78（58.2±5.7）岁。临床表现主要为胸闷、胸痛、咳嗽、咳痰咯血、痰中带血等。

由此可得免疫进化算法的进化操作:

1.1.3 基于免疫进化的粒子群算法

粒子群算法虽具有原理简单、算法容易等优点，但也存在初期信息素匮乏、易陷入局部最优解等一些不足之处.为此，笔者将粒子群算法与免疫进化算法有机地结合起来，利用后者的全局快速收敛性生成前者的初始解，赋予较优可行解一定的信息素，使得粒子群算法具有一定的后期爬坡能力.同时利用免疫进化的原理对信息素方程进行改进，使可行解跳出局部极值区间，提高全局的寻优能力，则得到:

在计算初期采用免疫进化算法进行全局搜索，根据粒子群算法设置的群体规模L确定免疫进化算法的进化代数K，使K=L，并将免疫进化算法中每次迭代产生的共L个较优解作为粒子群算法的初始路径.

1.2 模型求解

在灌区农业水资源优化配置的3层递阶结构模型(如图1所示)的基础上，对水量进行自上而下逐层寻优，得到灌区的最优种植比及各作物相应的优化灌溉制度.计算总体框架如图2所示.

2 实例分析

以引黄灌区75%枯水年为例，运用模型进行灌区内各作物间及其作物生育期内水量的优化配置.该区可利用地表径流0.15亿m3，由于地下水埋深较大，因此不考虑地下水补给量.根据引黄资料知该水平年可调控引黄净水量为1.188亿m3.该区土壤为壤土，孔隙率为50%，田间持水率为孔隙率的70%.灌区作物主要为小麦、玉米和棉花，其他参数详见表 1［7］.

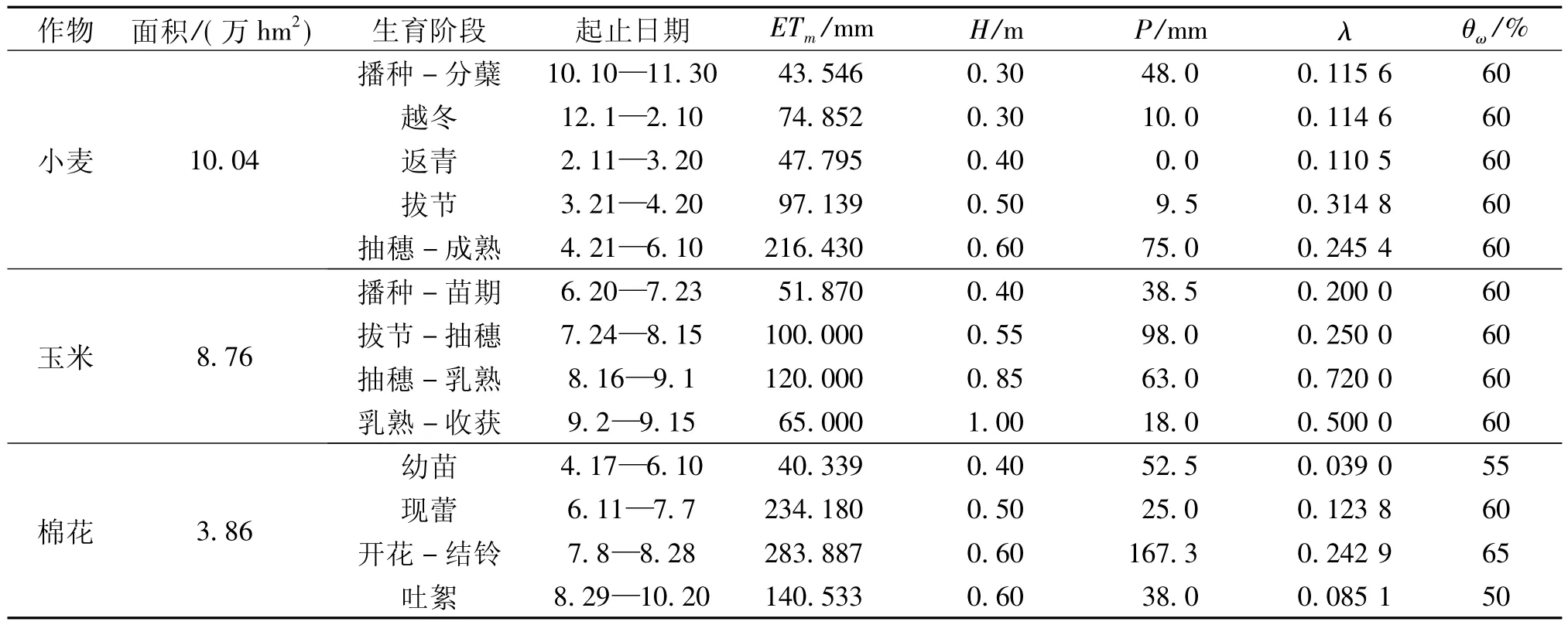
表1 作物生育阶段基本资料表

2.1 作物间水资源优化分配模型

在作物种植结构一定的条件下，以作物水分生产函数为依据［8］，将每种作物作为一个阶段，把有限的水量在多种作物全生育期之间进行分配.数学模型如下.

1)目标函数.以各作物的生产效益之和最大为目标，式中:ri(xi)为各作物全生育期的水分生产函数，通常采用二次抛物线形式;xi为各作物全生育期内单位面积上分得的水量;Ai为各作物的种植面积;αi为各作物单价;ωi为各作物效益分摊系数，一般冬小麦为 0.45，其他作物为 0.40［8］.

式中Q0为灌溉总水量.

2.2 单一作物水资源优化分配模型

以整个生育期的产量最大为目标，采用Jensen提出的在供水不足条件下，水量和农作物实际产量的连乘模型［6］作为作物水分生产函数，求解灌水量在作物各生育期的最优分配.数学模型如下.

1)目标函数.以单位面积的实际产量Ya与最高产量Ym的比值F最大为目标，

式中:ETak，ETmk分别为第k生育阶段的实际和最大蒸发蒸腾量［8］，mm;λk为作物对缺水的敏感性指数;Hk为第k生育阶段的计划湿润层深度，m;Pk，Kk分别为第k生育阶段的有效降雨量和地下水对计划湿润层的补给量;γ为土壤孔隙率，以占土壤体积的百分数计，%;Sk－1为第k生育阶段初计划湿润层内可供利用的水量，mm;θk为第k阶段计划湿润层内土壤平均含水率;θω为土壤含水率下限，以占孔隙率的百分数计，%.

2)约束条件为

式中:mk为单一作物第k生育阶段分配的水量;mkmax为作物第k生育阶段允许最大灌水量;T为作物总生育阶段数.

2.3 模型求解

按照笔者提出的算法进行模型求解，算法通过VB6.0语言实现，在程序中免疫进化算法种群规模N为200，进化代数K=L=20，粒子群算法中迭代步数为30，其他参数见文献［9］，计算结果见表2.

3 结语

合理的优化配置模型，以及兼顾计算精度与计算效率的模型求解方法是解决水资源优化配置问题的关键.传统粒子群算法虽然广泛应用，但存在初期信息素缺乏，易陷入局部最优解等不足.为此笔者利万m3用免疫进化算法的全局快速收敛性，在已有水资源配置模型的基础上，提出了免疫进化的粒子群混合算法，并将其应用于濮阳渠村灌区的农业水资源优化配置研究中.计算结果表明，该混合算法克服了传统算法中的不足，结果合理且计算方法较为简单，可为灌区水资源配置提供理论指导.

表2 优化配置结果

［1］徐刚，马光文，粱武湖，等.蚁群算法在水库优化调度中的应用［J］.水科学进展，2005，16(3):397 －400.

［2］陈曦，蒋加伏.免疫粒子群优化算法求解旅行商问题［J］.计算机与数学工程，2006，6(34):10 －13.

［3］王顺久，张欣莉，倪长健，等.水资源优化配置原理及方法［M］.北京:中国水利水电出版社，2007.

［4］Regulwar D G，Anand R P.Development of 3-D optimal surface for operation policies of a multi-reservoir in fuzzy environment using genetic algorithm for river basin development and management［J］.Water Resource Manage，2008，22(5):595－610.

［5］刘涵.水库优化调度新方法研究［D］.西安:西安理工大学，2006.

［6］李远华.节水灌溉理论与技术［M］.武汉:武汉水利电力大学出版社，1998.

［7］富可荣.灌区典型年水资源优化配置研究［D］.郑州:华北水利水电学院，2008.

［8］徐建新，陈南祥，黄强.区域水资源规划及灌区节水增产灌溉专家系统研制［M］.郑州:黄河水利出版社，2008.

［9］张军，詹志辉.计算智能［M］.北京:清华大学出版社，2009.

Application of Particle Swarm Optimization Based on Immune Evolution to Optimizing Allocation of Water Resources in Irrigated Areas

MA Jian-qin1，WEI Rui2，ZHANG Peng3
(1.North China Institute of Water Conservancy and Hydroelectric Power，Zhengzhou 450011，China;2.Yellow River Hydrological Survey and Design Institute，Zhengzhou 450004，China;3.The First Branch of Henan Lixin Management Consulting Co.，Ltd.，Zhengzhou 450006，China)

The particle swarm optimization based on immune evolution was proposed combining the existing optimal allocation model of water resources and this algorithm was applied to the optimal allocation of agricultural water resources of Puyang irrigated region.The calculation results showed that the compound algorithm had overcome the shortages of the existing algorithm which lacked initial information and easily fell into local optimal solutions in the solving process，and the results were reasonable and the calculation was simple.It could provide a theoretical basis and decision-making references for the optimal allocation of water resources in the irrigated areas.

irrigated area;water resources;optimal allocation;immune evolution algorithm;particle swarm optimization

1002－5634(2011)05－0035－04

2011－07－01

“948”资助项目(201047);国家自然基金资助项目(41071025);河南省骨干教师资助项目;2009年度河南省教育厅自然科学研究资助项目(2009A170004);河南省科技发展计划(092102310197);华北水利水电学院高层次人才启动项目(200514).

马建琴(1973—)，女，河南郑州人，教授，博士，硕士生导师，主要从事农业水资源可持续利用、区域水资源优化配置、节水农业等方面的研究.

(责任编辑:陈海涛)