多厢矩形渡槽槽身弹性稳定分析的梁壳复合有限条法

徐 伟，徐建国，王 博

(1.郑州大学 土木工程学院，河南 郑州 450001;2.郑州大学 水利与环境学院，河南 郑州 450001)

多厢矩形渡槽边墙、隔墙兼做纵梁，沿槽身纵向一定距离布有侧肋、横梁及拉杆，具有整体性好、刚度大、输水流量大等优点，是南水北调中线输水渡槽主选结构形式之一.随着高强混凝土及预应力技术的应用，槽身边墙、隔墙及底板的高厚比、宽厚比变得越来越大，在多种荷载组合作用下，横截面内存在较大的纵向压力及弯矩，在设计、施工乃至运行过程中，应充分考虑槽身稳定性问题［1］.

有限条法横向位移采用插值多项式函数，纵向采用解析函数代替常规有限元法的离散化方法，降低了结构维数，单元划分简单，输入数据少，适合于各种边界条件和加载条件，精度在求解板、壳和桥梁结构的静、动力计算及稳定分析中已得到验证［2－5］，不足之处在于对横截面形状不规则的复杂结构难以进行条元划分和结构计算，即使结构横截面形状规则，若条元内有横向加劲肋或条元间有横向连接拉杆，常规有限条法也较难解决.文献［6］采用梁壳复合有限条法计算渡槽自振特性，解决了条元内横向加劲肋及条元间横向连接拉杆的问题.针对渡槽槽身横截面形状规则的特点，本文基于最小势能原理，探讨应用梁壳复合有限条法分析多厢矩形渡槽槽身的弹性稳定问题.相对静力分析，弹性稳定分析时结构的总势能除弹性势能及外力势能外，还包括附加应变能［7］.

1 壳条的附加应变能

槽身弹性稳定分析属于小挠度问题，不考虑壳条中面位移引起的附件应变.弯曲引起的平面附加应变为［3］:

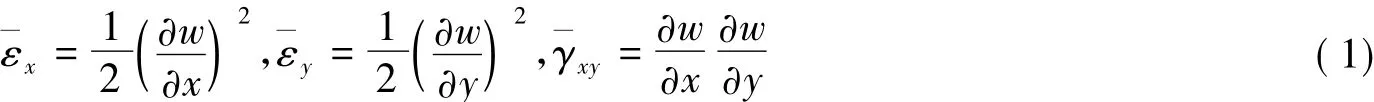
式中:w为壳条的弯曲挠度.

式中:t为壳条的厚度;Nx，Ny为壳条中面内拉压力;Nxy，Nyx为壳条中面内剪力.

弹性体内的应变能等于变形过程中外力所做的功，因此可通过计算中面内力在附加应变上所做的功来求得弯曲引起的附加应变能［8］:

引入形函数表示的壳条弯曲挠度［6］，则有:

式中:δs，m为壳条节线位移参数列阵［6］.两端简支时，矩阵 gs，m的具体形式如下:

式中:km=mπ/a;a，b为壳条长度和宽度;x，y为壳条局部坐标.由式(3)和(4)可得壳条的几何刚度矩阵:

其基本单位子矩阵为:

S为弹性稳定分析时壳条初始平面应力矩阵：

2 板内加劲肋的影响

槽身侧肋、横梁为边墙、底板的板内加劲肋，弹性稳定分析时，需考虑其对整体结构几何刚度的影响.用壳条节线位移参数计算壳条内梁单元节点位移的公式为［6］:

式中:T为位移转换矩阵，Tim，Tjm是与梁单元节点i，j对应的m项位移转换矩阵的子矩阵.

若空间梁单元在其局部坐标系中的几何刚度矩阵记为kbg，则用壳条节线位移参数表示的梁单元附加应变能为［9］:

可得壳条内梁单元在壳条节线位移广义坐标系中的几何刚度矩阵为:

3 梁壳复合有限条总势能

由弹性力学能量原理可求得壳条弹性势能Us，梁单元的弹性势能Ub及壳条外力势能W［6］，梁壳复合有限条总势能等于弹性势能、附加应变能及外力势能之和:

式中:ks为壳条刚度矩阵;为梁单元在壳条节线位移参数广义坐标中的刚度矩阵;qe为壳条分布荷载系数;n为一个梁壳复合有限条中梁单元的个数.

由式(13)得梁壳复合有限条的几何刚度矩阵为:

4 横向连接拉杆的处理

设编号为H的槽身壳条与拉杆相连，拉杆离散后与壳条相连的梁单元编号为E，节点为e和f，其中节点e为壳条节线上的一点.梁单元E节点位移与壳条H节线位移参数满足关系［6］:

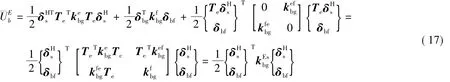
由上式可以看出，对于横向连接拉杆梁单元E的附加应变能可作如下描述:附加应变能由3部分组成，即与之相连接的壳条H引起的附加变形势能、梁单元节点f引起的附加变形势能，以及壳条H与梁单元E相互作用引起的附加应变能.整体结构计算时，梁单元E的节点f的位移作为整体结构的单独自由度来处理.计算所得的矩阵经坐标转换后，将其中的各元素计入整体几何刚度矩阵相应位置.

5 弹性稳定分析的基本方程

把局部坐标系内的节线位移、刚度矩阵及荷载转换到结构整体坐标系中去，然后利用编码法［10］可建立多厢矩形槽槽身整体的位移列阵、刚度矩阵和荷载列阵.设组集后槽身整体位移列阵为δ，刚度矩阵为K，几何刚度矩阵为KG，外荷载列阵为F.则整个结构的应变能等于各单元应变能之和:

由最小势能原理知势能的一阶变分等于0，得弹性稳定问题的基本方程:

弹性稳定临界状态的特点是:即使外荷载F=0，结构仍能维持一定的变位，即δ≠0.如果纵向荷载按比例因子λ增加，则如上方程即转换为弹性稳定分析的广义特征值问题［9］:

6 算例验证

6.1 算 例 1

某矩形薄板，长(a)、宽(b)均为2 m，厚度t为0.2 m，对边简支，沿宽度均匀承受60 MPa的纵向压力，弹性模量为3.25×107MPa，泊松比为0.167.为增强薄板的稳定性，可在薄板纵向或横向布置加劲肋.利用梁壳复合有限条法，沿宽度划分为5个壳条，计算不同长宽比时薄板的稳定系数，并与铁摩辛柯解［11］相比较，计算结果列于表1.

表1 薄板屈曲系数Tab.1 Buckling coefficients of thin plate

可见，本文解与铁摩辛柯解最大相对误差为0.036，说明应用梁壳复合有限条法分析加肋薄板的弹性稳定是适合的，精度满足工程计算要求.随着薄板长宽比的增加，稳定系数逐渐降低，就单根加劲肋而言，纵向加肋效果优于横向加肋.

6.2 算 例 2

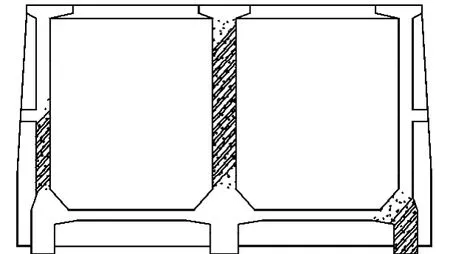
图1 槽身横截面Fig.1 Cross-section of aqueduct

南水北调中线双洎河渡槽初步设计槽身为预应力两厢矩形槽，单跨长30 m，设计水位为6.58 m，两端简支.每槽净宽7.0 m;边墙净高 7.9 m，厚 0.6 m;隔墙厚 0.9 m;底板厚0.4 m，沿槽身纵向每隔一段距离布有侧肋、横梁及拉杆.分别利用梁壳复合有限条法和ANSYS程序进行如表2所示的多工况下槽身的弹性稳定分析.应用ANSYS程序分析时，采用块体单元划分结构［12］，并进行了单元加密计算，以验证有限单元法的有效性.利用梁壳复合有限条法计算时，按照等效荷载法计算节线处预应力效应［13］.2种方法计算得出的各工况下槽身弹性稳定系数见表2.

通过对计算数据分析可得如下结论:

(1)梁壳复合有限条法计算多厢矩形槽槽身弹性稳定分析时具有与ANSYS程序分析相同的精度，可以作为有限元法的替代方法.

(2)理论上，计算级数m取值越大，计算精度越高.但实际计算中，随着级数项的增加，计算量也成倍增加，因此级数m的取值应以满足精度要求为准.算例中m取到25时精度已经足够.

(3)正常使用时，风荷载及人群荷载对槽身内有横向拉杆弹性稳定影响不大.

(4)随着槽内水位的增加，槽身弹性稳定系数降低，但屈曲模态没有变化.图2(a)绘出了工况5一阶屈曲模态的水平面投影，工况2，3，4与之相同.

(5)图2(b)绘出了工况1一阶屈曲模态的水平面投影，对比图2(a)和(b)知:预应力作用不仅降低了槽身弹性稳定系数，而且一阶屈曲模态也发生了变化，说明在预应力逐步作用过程中，槽身结构体系受力状况发生了转变.

(6)各种计算工况下结构自身并无变化，只是荷载情况不同，表2计算结果的差异主要是由荷载矩阵计算形式不同引起的.

表2 计算工况及槽身弹性屈曲系数Tab.2 Working cases and buckling coefficients of aqueduct

图2 槽身屈曲模态Fig.2 Buckling mode of aqueduct

7 结语

应用梁壳复合有限条法计算多厢矩形渡槽槽身弹性稳定时，具有单元划分简单、数据输入少、计算效率高的优点，精度满足工程要求.算例2所选渡槽为实际工程设计方案，在正常使用状况下弹性稳定系数较大，不会发生失稳破坏.施工过程特别是槽身预应力张拉过程中的稳定性问题及动力稳定性问题应作进一步研究.

［1］白新理，马文亮.大型预应力梁式薄壳渡槽整体稳定性分析［J］.水利与建筑工程学报，2008，6(3):12-14.(BAI Xinli，MA Wen-liang.Global stability analysis of large-scale prestressed beam thin-shell aqueduct［J］.Journal of Water Resources and Architectural Engineering，2008，6(3):12-14.(in Chinese))

［2］CHEUNG Y K，KONG J.Virbration and buckling of thin-walled structures by a new finite strip［J］.Thin-Walled Structures，1995，21:327-343.

［3］BRADFORD M A.Elastic local buckling of steel plates in composite steel-concrete members［J］.Engineering Structures，1996，18(3):193-200.

［4］BRADFORD M A，AZHARI M.Buckling of plates with different end conditions using the finite strip method［J］.Computers＆Structures，1995，56(1):75-83.

［5］杨开云，张多新，白新理，等.柱壳有限条元法在预应力U型薄壳渡槽稳定性分析中的应用［J］.水利学报，2006，37(5):598-602.(YANG Kai-yun，ZHANG Duo-xin，BAI Xin-li，et al.Cylinder shell finite strip element method for stability analysis of prestressed U-shaped thin shell aqueduct［J］.Journal of Hydraulic Engineering，2006，37(5):598-602.(in Chinese))

［6］徐伟，王博.基于梁壳复合有限条法的矩形渡槽自振特性分析［J］.武汉理工大学学报，2010，32(9):323-327.(XU Wei，WANG Bo.Free vibration analysis of rectangle aqueducts based on beam-shell compound finite strip method［J］.Journal of Wuhan University of Technology，2010，32(9):323-327.(in Chinese))

［7］OVESY H R，LOUGHLAN J，GHANNADPOUR S A M，et al.Geometric non-linear analysis of box sections under end shortening，using three different versions of the finite-strip method［J］.Thin-Walled Structures，2006，44:623-637.

［8］CHEUNG Y K，AU F T K，ZHENG D Y.Finite strip method for the free vibration and buckling analysis of plates with abrupt changes in thickness and complex support conditions［J］.Thin-Walled Structures，2000，36:89-110.

［9］朱伯芳.有限单元法原理与应用［M］.北京:中国水利水电出版，2004:27-31.(ZHU Bo-fang.The finite element method theory and application［M］.Beijing:China WaterPower Press，2004:27-31.(in Chinese))

［10］吴鸿庆，任侠.结构有限元分析［M］.北京:中国铁道出版社，2000:19-26.(WU Hong-qing，REN Xia.The finite element method of structures analysis［M］.Beijing:China Railway Publishing House，2000:19-26.(in Chinese)).

［11］TIMOSHENKO S P，GERE J M.Theory of elastic stability［M］.New York:McGraw Hill，1970.

［12］李晓克，赵晴天，赵顺波.大型墙梁式渡槽二次预应力施工过程分析研究［J］.水利水运工程学报，2009(1):59-65.(LI Xiao-ke，ZHAO Qing-tian，ZHAO Shun-bo.Analysis of two-time prestressing construction of aqueduct with large wallbeams［J］.Hydro-Science and Engineering，2009(1):59-65.(in Chinese))

［13］唐纯喜.长距离输水工程的关键结构体系可靠度研究［D］.杭州:浙江大学，2007.(TANG Chun-xi.Study on system reliability of key structures of long-distance water transfer project［D］.Hangzhou:Zhejiang University，2007.(in Chinese))