蓄滞洪区洪水演进数学模型研究及应用

李大鸣，管永宽，李玲玲，吕会娇，王 强

(1.天津大学 建筑工程学院暨港口与海洋工程教育部重点实验室，天津 300072;2.水利部海委引滦工程管理局，河北 迁西 064309)

蓄滞洪区是防洪减灾体系中的重要组成部分，通过适时分蓄超额洪水、削减洪峰，基本保障中下游重要城市和重要防洪地区的安全，为流域防洪减灾做出了巨大贡献.为降低洪水造成的损失，各国在加强防洪工程措施建设的同时也大力进行非工程措施研究.洪水演进数值模拟是非工程措施的重要组成部分，是绘制洪水风险图、洪水预警预报等的重要依据.

对洪水演进的模拟，国内外的专家进行了不少研究，分别通过差分法、有限元法、有限体积法对洪水演进进行模拟.J.A.Liggett等［1］利用显式有限差分法和矩形网格建立了最早的二维模型;R.Garcia等［2］建立有限差分法模型，较好地处理了非线性项的问题.刘树坤等［3］用显格式差分法模拟了小清河分洪区洪水;童汉毅等［4］用破开算子与贴体坐标变换的方法，计算了平面二维控制方程的格式离散条件下的水动力问题;T.Tucciarelli等［5］建立了解扩散方程的有限元模型;李大鸣等［6－7］用质量加权集中的有限元法计算了河道二维洪水演进;谭维炎［8］提出二维浅水明流的二阶格式，将其应用于长江中下游洞庭湖防洪系统的水流模拟;王海船［9］将一维、二维模型相结合，采用直角坐标下非均匀矩形网格的控制体积法模拟流域洪水.

本文以二维非恒定流方程为基本理论，采用有限体积法对网格进行离散求解.模型根据恩县洼蓄滞洪区的实际地形、地貌和洪水调度方案，模拟了自然滞洪和分区滞洪两种情况下的洪水演进过程，对淹没范围、淹没水位、蓄水量进行了验证;提出了在大尺度网格基础上考虑公路模化的方法;研究了公路建设中路基占用空间、涵洞尺度、取土方量等因素对蓄滞洪区淹没范围、淹没水位的影响;探讨了风波在蓄滞洪区分洪时产生水面壅高的问题，得出了风波与水面壅高的基本关系.

1 数学模型基本理论

1.1 基本方程

连续方程:

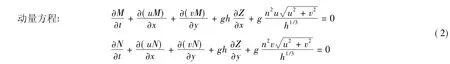
式中:H为水深;t为时间;Z为水位，Z=Z0+H，Z0为底高程;q为源汇项;M，N分别为x，y方向上的单宽流量，且M=Hu，N=Hv;u，v分别为x，y方向的平均流速;n为糙率;g为重力加速度.

1.2 有限体积离散

按照有限体积法布置二维网格(图1)，取单元网格为控制体，在网格中心处计算水位H，在网格周边通道的中点处计算流量Q.即在平衡计算时，沿控制体每一边的法向通量用该边中点处的通量作代表，乘以边长即为通量沿该边的积分.中点的通量可用中心格式(如取相邻两格子形心处通量的平均)或逆风格式确定.则将方程(1)改写成矢量形式，按照有限体积法，将其在控制体内进行积分，对水位H和流量Q按时间交错计算方式计算(图2).则方程(1)可离散为

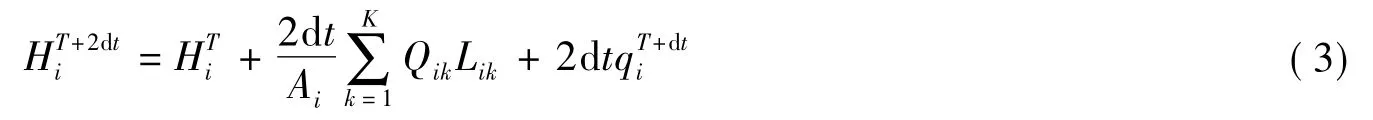
式中:Ai为第i个网格的单元面积;Lik为i号网格的第k号通道的长度;Qik为i号网格的第k号通道的单宽流量.

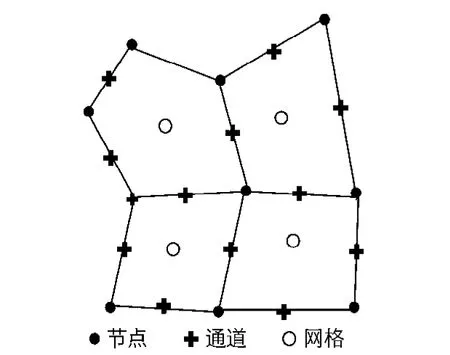
图1 H和Q的空间布置Fig.1 Space arrangement plan of H and Q

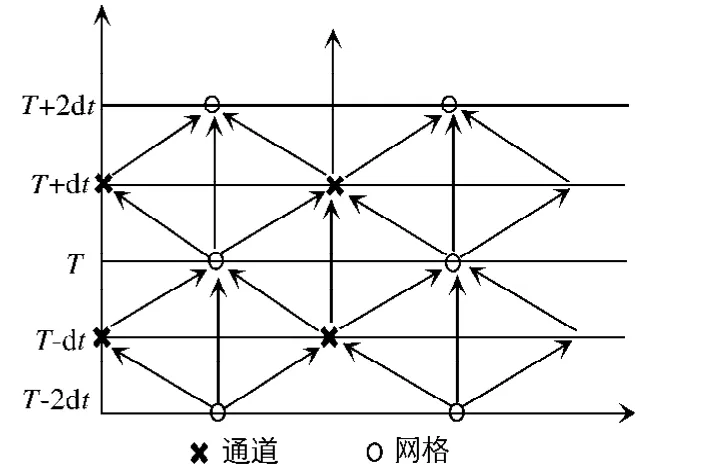
图2 H和Q的时间交错计算方式Fig.2 Time arrangement plan of H and Q

1.3 数值通量计算

考虑到滞洪区内各种地形条件及铁路、公路等建筑物情况，本模型将所有单元间的通道按不同情况进行分类，概化为地面型通道、河道型通道、特殊通道和连续堤或缺口堤通道进行处理，并给所有通道附加特征信息，以相应的水力学公式进行通量计算［10－11］.

(1)地面型通道，通道两侧单元为陆地且其内没有阻水建筑物.重力和阻力为地面洪水演进的主要影响因素，利用差分方法离散得到下述方程:

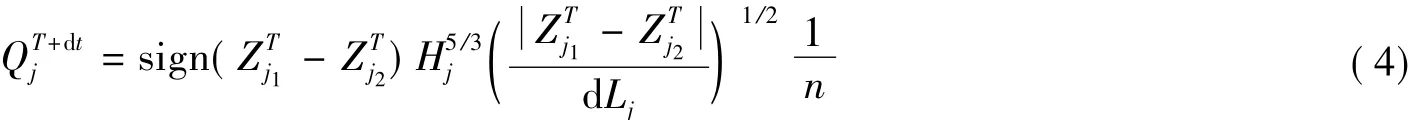
(2)河道型通道，通道两侧单元为河道.重力、阻力和加速度为河道洪水演进的主要影响因素，利用差分方法离散得到下述方程:

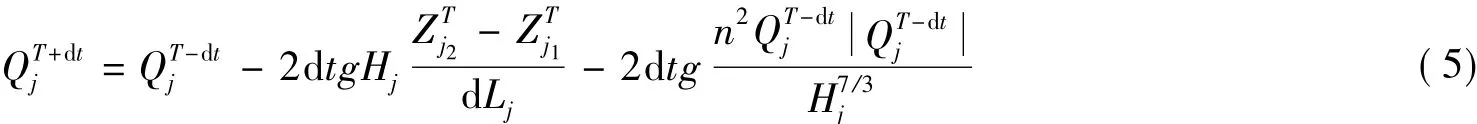
(3)漫堤型河道通道，滞洪区内有宽度较小的河流(尺寸达不到独立单元的标准)，部分河道因为没有堤防工程或堤防工程标准较低，导致滞洪区在蓄滞洪水过程中河道内水流与两岸陆地水流产生水量交换的情况，这种通道可概化为具有高度和长宽尺寸的特殊通道.采用连续方程来计算特殊通道中的水位.

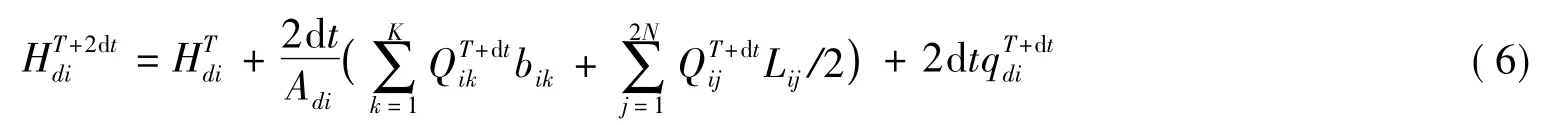
式中:Hdi，Adi分别为特殊单元的平均水深和面积;∑Qk，∑Qj分别为特殊通道上的流量及通道与网格间交换的各流量之和;qd为特殊单元的源汇项;b为通道宽度;L为通道长度.

(4)连续堤或缺口堤通道，对于高于地面的阻水建筑物，如堤防、铁路等概化成连续堤或缺口堤通道，其流量采用宽顶堰溢流公式来计算，离散后得到:

1.4 公路模化

滞洪区模型计算网格尺度一般为几百米以上，而德商公路宽度为几十米(图3)，为在模型大尺度网格上考虑公路工程建设后的影响，考虑公路建设后形成的不透水堤、涵洞堤等不同的阻水建筑物形式，将公路沿单元通道模化，将公路宽度占用的空间平分到通道两侧的单元上，减小了两侧单元的蓄水面积，同时考虑到公路修筑时在路基两侧取土形成的取土沟会增加单元的蓄水量，将各单元取土方量折合为单元底高程变化，对单元底高程重新模化(图4).同时沿公路通道分布的透水涵洞，根据公路里程将桥涵长度模化到通道上，使德商公路建设前后滞洪区洪水演进模拟条件更接近实际情况.

图3 公路路基剖面(单位:m)Fig.3 Cross section of roadbed

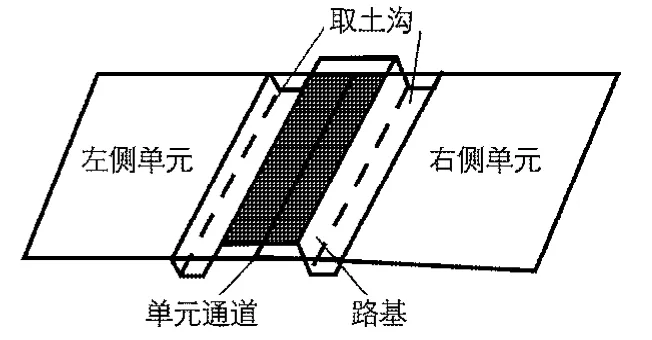
图4 公路路基模化示意图Fig.4 Schematic diagram of roadbed

1.5 风波计算

本模型特别考虑了蓄滞洪区使用时区域内产生的强风对洪水壅高的影响.风波计算采用莆田站方法［12－14］的预报公式

风速取水面以上10 m处的风速值，平均水深为滞洪区蓄水后公路路基附近平均水深，风距为沿风向路基至隔堤间水面宽度.

2 洪水演进数学模型的建立

2.1 恩县洼滞洪情况简介

恩县洼滞洪区是漳卫南运河流域中卫运河下游右岸附近的天然洼地，是黄河故道左岸河滩高地与运河相互作用形成的封闭碟形洼地，洼地三面环堤，四周高中间低，历史上称高鸡泊(图5).1954年6月水利部决定将恩县洼辟为滞洪区，当年启用2次分洪，2次共滞蓄水量1.4亿m3.次年洪水来临再次启用，滞蓄水量1.7亿m3.1963年漳卫河发生特大洪水，再次利用恩县洼滞洪，蓄水量6.99亿m3，滞洪期间曾遇6～7级大风和暴雨.

2.2 网格剖分及滞洪区划分

模型基本网格采用0.3 km×0.3 km网格，考虑河道、公路和堤防的曲线和不规则轮廓将网格划分为任意形状，模型网格采用程序自动划分、逐级加密、分区优化的剖分方法，生成网格结点4 593个，网格单元4 401个，网格通道8 993个(图6).图6中彩色多边形表示村庄等高地，贯穿滞洪区范围黑色线条表示拟建公路(德商公路及支线)，模型入流条件是洪水通过西郑庄分洪闸经导流堤进入恩县洼滞洪区，牛角峪为退水闸.模型中村庄以地形高度和糙率变化来表现，公路、堤坝和河道以通道高程变化来表现.

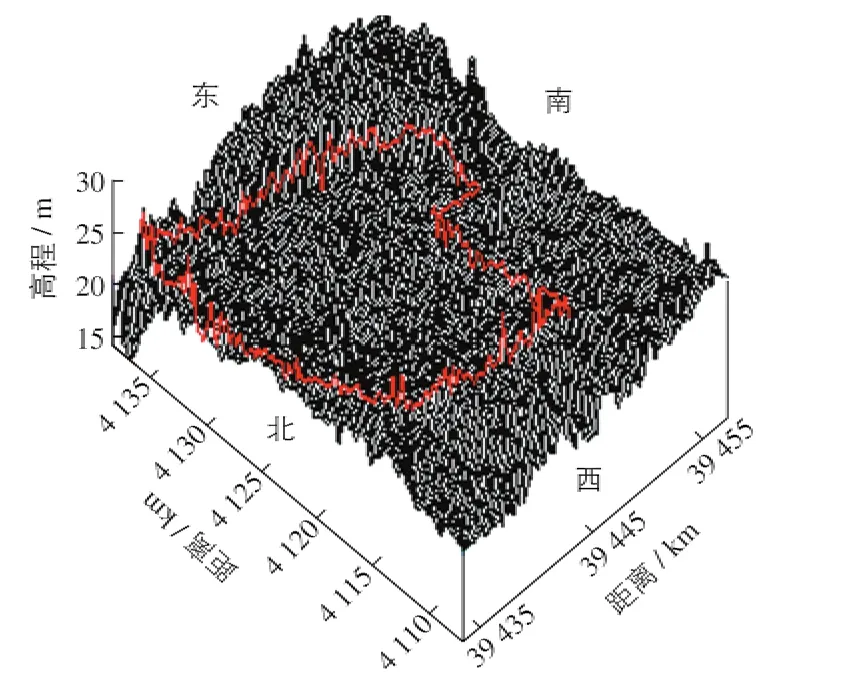
图5 恩县洼地形三维分布Fig.5 3D map of Enxianwa

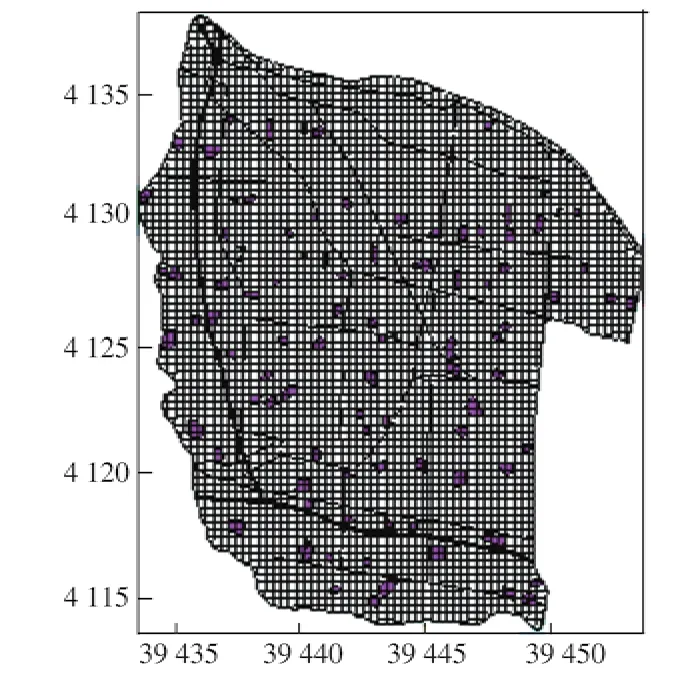
图6 恩县洼模型网格剖分Fig.6 The grids of Enxianwa model

2.3 模型边界条件

恩县洼模型入流边界为西郑庄分洪闸，出流边界为牛角峪退水闸.分洪流量过程采用1963年型洪水过程和漳河、南陶河百年一遇洪水(以下简称“南陶1%频率”)，卫河相应的流量过程和退水边界流量为零过程.在恩县洼滞洪区内德商公路主线、支线路面高程均在25.0 m以上，高于最大滞洪水位，模型将路基处理为不过流堤坝，涵洞沿公路分布在路基上，模型将涵洞处理为具有大孔口出流的通道.恩县洼洪水演进模型采用分区综合糙率，公式为

式中:ni为各典型区域糙率，过水下垫面为村庄、林地、旱地、河道主槽和河道滩地时的相应糙率分别为0.065，0.045，0.030，0.023 和 0.027;Ai为各典型区域面积.

2.4 模型调试

1963年型洪水蓄水量15 465.6万m3介于1954年和1955年洪水之间，蓄水水位、淹没范围具有可比性，因此选择其进行模型调试.通过模型计算得出水位、淹没面积、蓄水量见表1.

模型得出1963年型洪水淹没面积介于1955年洪水和1954年洪水淹没面积之间，说明本模型计算合理(见图7).从模型洪水演进过程看，洪水通过导流堤向滞洪区中部低地汇流，并沿洼地向东部六五河附近汇集，在陈公堤阻挡作用下，沿堤向西和北两个方向扩散，直至充满高程在24.6 m以下的洼地.通过洪水演进模型模拟滞洪过程的各物理量变化过程定性、定量基本正确，可以用于模拟滞洪区洪水演进.

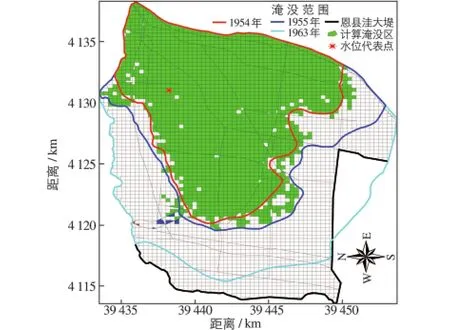
图7 模型计算与实际淹没范围比较Fig.7 Comparison between the calculated and the actual inundated area

表1 历史洪水与模型调试结果比较Tab.1 Comparison between the historic floods and the simulated results by model

2.5 百年一遇洪水演进模拟

根据卫河琪门站还原的1963年洪水过程及50年一遇、百年一遇设计洪水过程得到恩县洼不同情况分洪流量过程(图8).可以看出，漳河、南陶百年一遇(卫河相应)洪水过程产生的恩县洼流量过程最大，相应产生的蓄水量也最大.因此，选择漳河、南陶百年一遇(卫河相应)洪水过程为模拟对象，模拟其淹没区域及洪水演进过程.

模型入流条件是洪水通过西郑庄分洪闸，经导流堤进入恩县洼滞洪区，模拟选择漳河、南陶1%频率卫河相应的洪水流量过程，模拟0～238 h的流量过程，其中有流量时段为192 h，其余时段为后期蓄水水位自动调整时间.

选取20，40，100和230 h的洪水淹没范围图演示洪水演进过程(图9).从模型洪水演进过程看，洪水通过导流堤向滞洪区中部低地汇流，并沿洼地向东部六五河附近汇集，在陈公堤阻挡作用下，沿堤向西和北两个方向扩散，直至充满高程在24.6 m以下的洼地.通过洪水演进模型模拟滞洪过程的各物理量变化过程定性、定量基本正确，可以用于模拟滞洪区洪水演进.

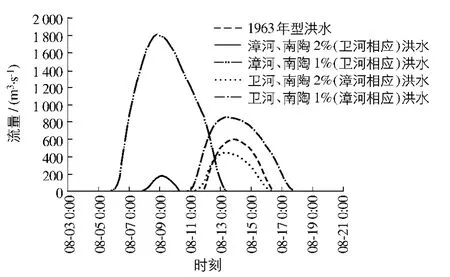
图8 恩县洼不同情况分洪流量过程Fig.8 Discharge hydrograph of flood diversion in different condition of Enxianwa

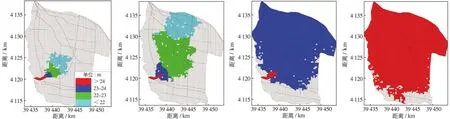
图9 漳河、南陶1%(卫河相应)模型洪水淹没过程Fig.9 Flood inundation process at flood frequency of one percent for Zhang River and Nantao River

选取1963年洪水为漳河、南陶百年一遇(卫河相应)洪水模型的验证案例.1963年洪水是在四女寺西破堤，向洼内自然倒坡分洪，虽然入流条件不同，但模型计算结果与1963年蓄水水位、淹没范围、蓄水量调查统计结果显示二者具有验证效果，经模型计算与1963年实际洪水调查统计结果相比较，两者水位分别为24.709和24.7 m，淹没面积分别为300.98和320 km2，蓄水量分别为68 221.4和70 000万m3;可见，模型计算结果与实际调查值基本一致.在重要的验证指标淹没范围上，模型计算与1963年实际淹没基本相符(见图10).因此，认为该模型构建合理，模型参数选择基本正确.

2.6 分区滞洪百年一遇洪水演进模拟计算

根据滞洪区需要分洪量，分别启用各个分洪区，尽量减少不必要的滞洪损失.以中部较大地带的185 km2为第Ⅰ区，其余116 km2为第Ⅱ区，结合区内具体情况，将Ⅰ区分为Ⅰ1和Ⅰ2小区，将Ⅱ区分为Ⅱ1，Ⅱ2，Ⅱ3和Ⅱ4共4个小区，各区位置和隔堤名称如恩县洼分区滞洪各区分布图(图11)，分区运用的顺序为Ⅰ1—Ⅰ2—Ⅱ1—Ⅱ2—Ⅱ3—Ⅱ4.

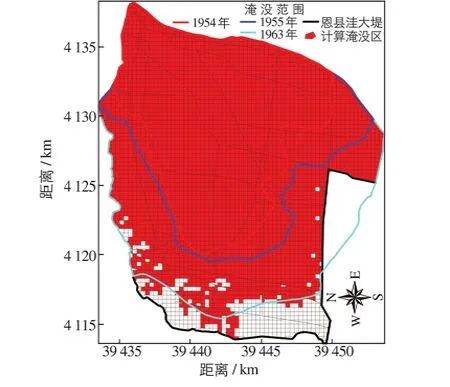
图10 漳河、南陶1%(卫河相应)模型计算与实际淹没范围比较Fig.10 Comparision between the calculated and the actual inundated area at flood frequency of one percent for Zhang River and Nantao River

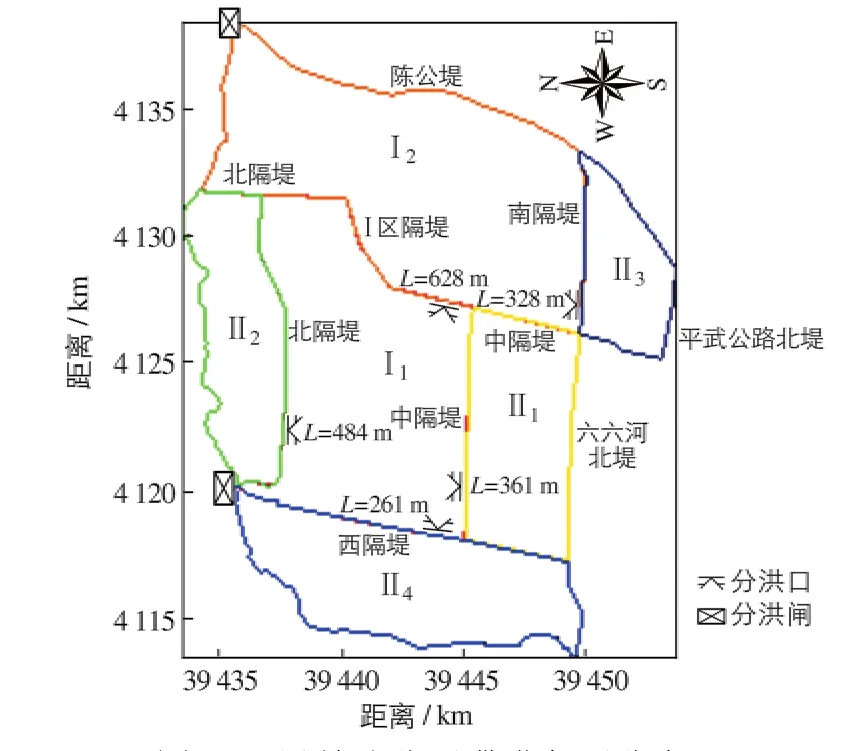
图11 恩县洼分区滞洪各区分布Fig.11 Distribution of divisional flood detention area of Enxianwa

分区滞洪分洪边界条件的位置和洪水过程与自然滞洪条件相同，仍采用漳河、南陶1%(卫河相应)洪水过程，以各区蓄水量为自溃堤溃决条件.模型模拟流量过程0～230 h，分别选取30，70，125和230 h的区域淹没作为演示洪水的演进过程(图12).

模拟的结果为滞洪区的调度管理提供了决策依据，为减轻滞洪区经济损失提供了较为科学可行的方法.

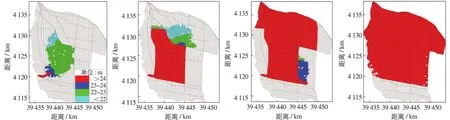
图12 分区使用时漳河、南陶百年一遇洪水演进淹没过程Fig.12 Flood routing process at the frequency of one percent for Zhang River and Nantao River in partition

3 公路建设前后模拟计算结果

3.1 公路建设后洪水演进

应用滞洪区洪水演进模型计算模拟了恩县洼内修建德商公路主线和支线前后洪水演进的变化.以漳河、南陶百年一遇洪水演进为公路建设前的工程情况，在此基础上考虑因公路建设使面积减小、沿公路通道分布透水涵洞，根据公路里程将桥涵长度模化在通道上，得出公路建设前后滞洪区水面平稳后模型计算结果:水位分别为24.709 和24.713 m，淹没面积300.98 和300.14 km2，蓄水量均为68 221.4 万 m3;工程后水位上升0.004 m，淹没面积减小0.84 km2.入流流量过程、蓄水水位变化过程、蓄水面积变化过程、蓄水量变化过程见图13.由于工程前后滞洪区水面平稳后水位、淹没面积变化不大，所以修筑这2条公路对蓄滞洪区蓄水量无明显影响.

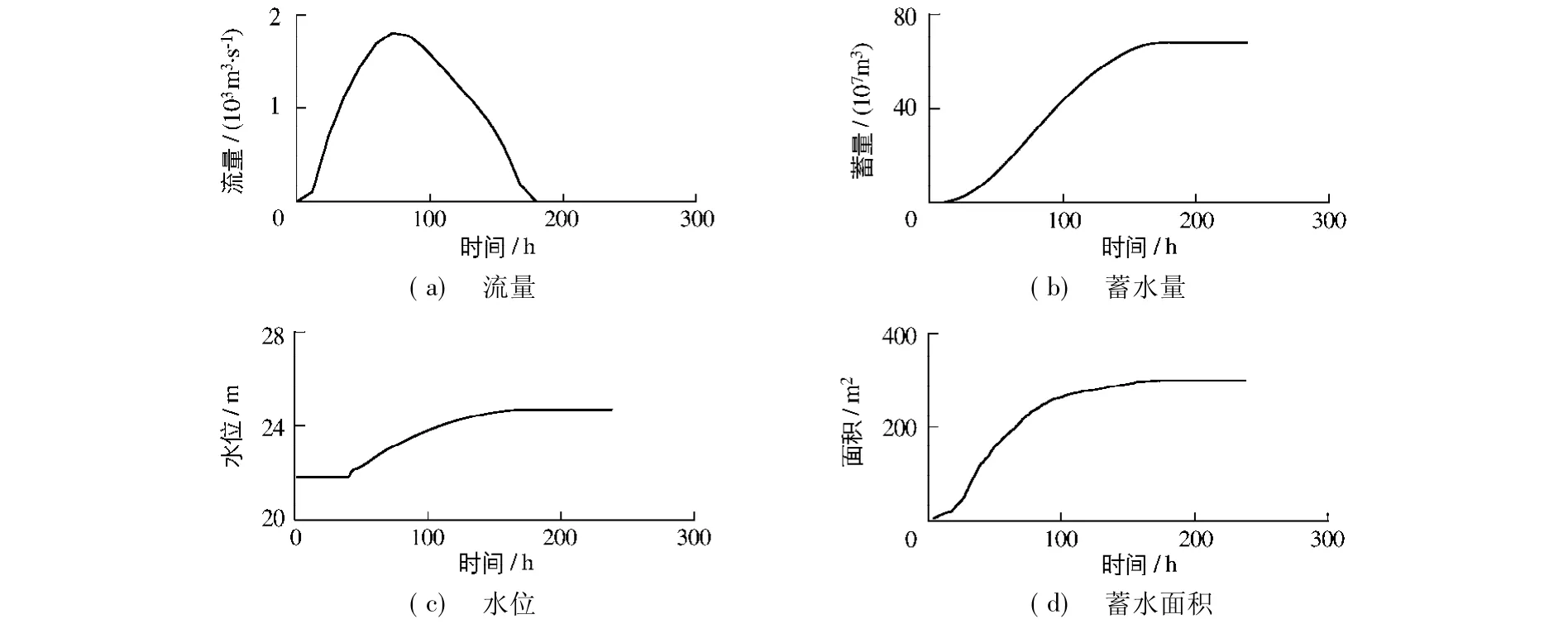
图13 修筑公路后漳河、南陶1%(卫河相应)洪水演进主要物理量变化过程Fig.13 The main physical quantities changing process in flood routing process at the frequency of one percent for Zhanghe River and Nantao River

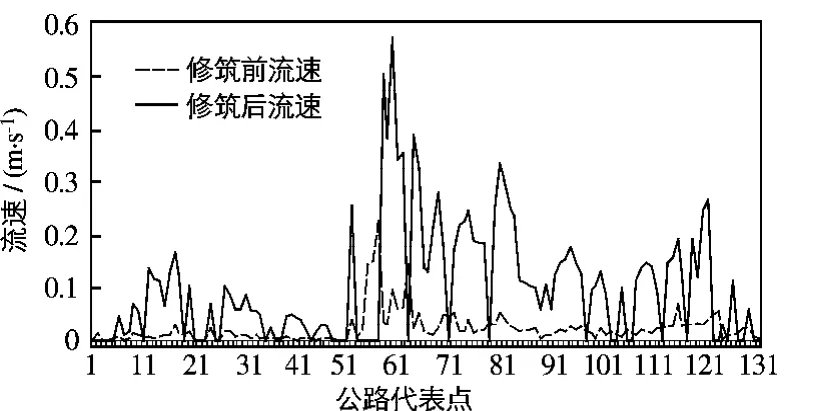
图14 公路修建前后路基当地流速比较Fig.14 Local velocity comparison before and after the road completion

由公路修建前后路基当地流速比较(图14)可见:修建前公路沿线最大流速约为0.23 m/s，修建后最大流速约为0.58 m/s，均发生在六五大桥附近.公路修建后流速增大，但最大增值为0.35 m/s.

3.2 风波对自然滞洪蓄水壅高的影响

在自然滞洪情况下，滞洪区蓄水达到平整后的高水位时，如果出现正对公路侧面10 m/s的强风作用，蓄滞洪水会产生较大的波高.因此，需要考察公路修建后风力作用下水面产生的波浪对公路的影响.

采用蒲田站方法预报平均波高，同时参考海岸动力学中的平均波高与1/10大波和1%大波的波高关系，推算出沿公路侧面的最大吹程在平均水深、最大水深条件下的平均波高，给出了平均水深的平均波高对应的1/10大波和1%大波的波高，分别对德商公路(东风)及支线公路(南风)进行计算，得出德商公路在此条件下最大波高为0.758 m，德商支线公路最大波高为0.437 m(图15).

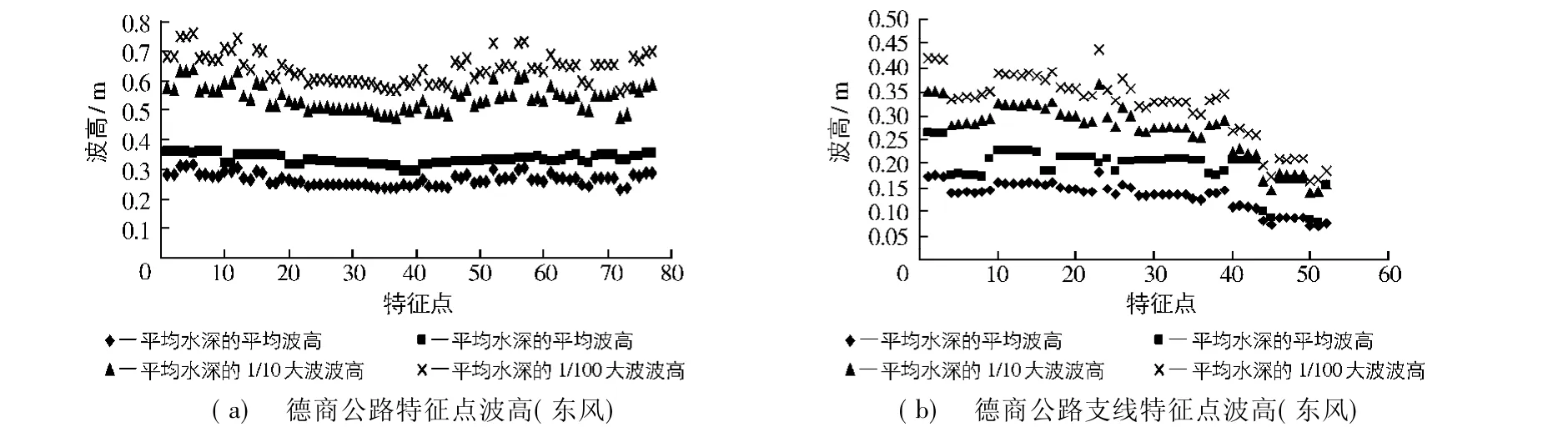
图15 德商公路特征点波高Fig.15 Wave height at characteristic points of Deshang highway

漳河、南陶1%(卫河相应)洪水的最大滞洪水位为24.713 m，公路高程一般为25 m，因此，德商及支线公路在此极端情况下，易遭到损坏，建议公路高程加高0.5 m，保证公路最低高程大于25.5 m;或者增加公路防浪墙设施，保证公路在极端条件下正常使用.

4 结语

采用1963年型洪水和漳河、南陶1%(卫河相应)洪水过程，对1954年、1955年和1963年洪水水位、淹没面积、蓄水量和淹没范围进行了模拟验证，表明模型设置合理，参数选择基本正确，模型计算结果可靠.通过模型计算，模拟洪水演进过程，动态演示淹没过程，为滞洪区的防洪及减灾提供了决策依据.

根据恩县洼滞洪区分区滞洪规划方案，将滞洪区共分为两大区，下辖六小区，通过滞洪水量控制，依据不同滞洪洪水量依次启用滞洪区域，模拟洪水分区演进过程，洪水演进工程与规划方案一致.

本文提出了公路建设在模型中的模化方法，模型模拟了滞洪区建设公路前后的洪水演进、蓄滞洪量、淹没范围和蓄水水位，考虑建设公路取土导致蓄水能力增加的工程情况，比较了公路建设后对洪水演进的水流速度、淹没范围、蓄水量和水位的影响，为同等条件下滞洪区内工程建设提供了研究思路.

模型选择漳河、南陶1%(卫河相应)洪水过程和10 m/s的强风同时发生条件下的洪水演进模拟，最大波浪高度约为0.8 m，说明滞洪区内公路建设后在蓄水达到平衡时受风波影响较大，因此应考虑加高公路路基或修筑公路路基防浪设施.

［1］LIGGETT J A，WOOLHISER D A.Difference solutions of the shallow-water equation［J］.J Engrg Mech Div，ASCE，1967，93(2):39-71.

［2］GARCIA R，KAHAWITA R A.Numerical solution of the St.Venant equations with the MacCormack finite difference scheme［J］.Int J Numer Methods Fluids，1986(6):507-527.

［3］刘树坤，李小佩，李士功，等.小清河分洪区洪水演进的数值模拟［J］.水科学进展，1991，2(3):188-192.(LIU Shukun，LI Xiao-pei，LI Shi-gong，et al.Numerical simulation of flood routing in the Xiaoqinghe flood plain［J］.Advances in Water Science，1991，2(3):188-192.(in Chinese))

［4］童汉毅，赵明登，槐文信，等.洪潮遭遇情况的水动力学计算［J］.武汉水利电力大学学报，2000，33(5):11-15.(TONG Han-yi，ZHAO Ming-deng，HUAI Wen-xin，et al.Hydrodynamic calculation for flood meeting with tide［J］.Journal of Wuhan University of Hydraulic and Electric Engineering，2000，33(5):11-15.(in Chinese))

［5］TUCCIARELLI T，TERMINI D.Finite-element modeling of flood plain flow［J］.J Hydraulic Engineering，2000，126(6):416-424.

［6］李大鸣，陈虹，李世森.河道洪水演进的二维水流数学模型［J］.天津大学学报，1998，31(4):439-446.(LI Da-ming，CHEN Hong，LI Shi-shen.A 2-D numerical model of propelling flood in the river［J］.Journal of Tianjin University，1998，31(4):439-446.(in Chinese))

［7］范玉，陈建，李大鸣.一、二维洪水演进数学模型在滞洪区的应用［J］.华北水利水电学院学报，2009，30(4):12-15.(FAN Yu，CHEN Jian，LI Da-ming.Application of flood wave advance numeric modeling of one dimension and two dimensions in flood detention area［J］.Journal of North China Institute of Water Conservancy and Hydroelectric Power，2009，30(4):12-15.(in Chinese))

［8］谭维炎，胡四一，王银唐，等.长江中游洞庭湖防洪系统水流模拟［J］.水科学进展，1996，7(4):336-345.(TAN Weiyan，HU Si-yi，WANG Yin-tang，et al.Flow modelling of the middle Yangtze River-Dongting lake flood control system［J］.Advances in Water Science，1996，7(4):336-345.

［9］王海船，李光炽.流域洪水模拟［J］.水利学报，1996(3):44-50.(WANG Chuan-hai，LI Guang-zhi.The model of basin flood［J］.Journal of Hydraulic Engineering，1996(3):44-50.(in Chinese))

［10］李大鸣，林毅，徐亚男，等.河道、滞洪区洪水演进数学模型［J］.天津大学学报，2009，42(1):47-55.(LI Da-ming，LING Yi，XU Ya-nan，et al.Numerical model of flood propagation of rivers and flood detention basin［J］.Journal of Tianjin University，2009，42(1):47-55.(in Chinese))

［11］LI Da-ming，ZHANG Hong-ping，LI Bing-fei，et al.Basic theory and mathematical modeling of urban rainstorm water logging［J］.Journal of Hydrodynamics(Ser B)，2004，16(1):17-27.

［12］薛鸿超，顾家龙，任汝述.海岸动力学［M］.北京:人民交通出版社，1980:166-168.(XUE Hong-chao，GU Jia-long，REN Ru-su.Coastal hydrodynamics［M］.Beijing:China Communications Press，1980:166-168.(in Chinese))

［13］洪广文，杨正己.风浪要素计算方法［J］.水利水运科技情报，1978(3):25-67.(HONG Guang-wen，YANG Zheng-ji.The calculation method of waves element［J］.Water Conservancy and Water Transportation Science and Technology Information，1978(3):25-67.(in Chinese))

［14］杨正己.水库风浪计算方法［J］.水利水运科学研究，1983(3):92-104.(YANG Zheng-ji.The calculation method of wave reservoirs［J］.Journal of Nanjing Hydraulic Research Institute，1983(3):92-104.(in Chinese))