基于多种群混合遗传算法的车间实时调度系统

成国煌,夏胜雄,王 宇,2,严 睿

(1.武昌船舶重工有限责任公司,湖北 武汉 430060;2.华中科技大学,湖北 武汉 430074)

基于多种群混合遗传算法的车间实时调度系统

成国煌1,夏胜雄1,王 宇1,2,严 睿1

(1.武昌船舶重工有限责任公司,湖北 武汉 430060;2.华中科技大学,湖北 武汉 430074)

针对某船厂管子加工车间的实际情况,采用动态柔性调度技术,构建实时反馈调度模型,建立基于多种群混合遗传算法的车间实时调度系统,把动态连续的调度问题变成分块的静态调度问题,使动态问题静态化。针对调度问题的求解特点,提出基于多种群粒子群的混合遗传算法的任务调度算法。运用上述理论和算法,通过仿真和实际应用,结果表明该实时调度系统的有效性和合理性。

遗传算法;粒子群优化;车间调度;实时调度系统

0 引 言

目前,全球造船行业已经由典型的资金密集型、劳动密集型传统行业转变为资金密集、劳动密集和技术密集相互并重的高新行业。因此,加快造船企业信息空间工程建设,利用信息技术构造基础软件平台,建立智能化的并行协同生产模型,从而实现企业行为模式的变革,全面提升企业的竞争力。而且,由于现代造船企业趋向于总装厂方向发展,其主要任务将是船体制造和管子生产。而管子制造是一个多工种的复合工程,船用管子数量多,品种规格复杂,其材质、形状和尺寸等完全一样的极少,单项加工技术的提高并不能很大程度地提高管子的生产效率,因此管子的生产往往会成为造船中的瓶颈,所以研究管子的生产调度技术,提高管子生产效率是造船技术的一个重要问题。

车间柔性调度问题多是NP难题,现有的调度算法主要包括物理规划和模拟退火(simulated annealing,SA)、禁忌搜索算法 (taboo search,TS)、蚁群算法(ant system,AS)、遗传算法(genetic algorithm,GA)、粒子群优化 (particle swarm optimization,PSO)和混合算法等,但各种算法都有自己的优点和不足[1-3]。本文结合某船厂管子加工车间数字化生产的实际需要,按照车间现用的生产模式,通过采用多种群混合遗传算法的周期调度策略,解决实时反馈调度中的重调度问题,形成实时调度的柔性计划调度技术,使得车间具备处理突发事件的能力,提高船舶制造企业的生产效率。

1 实时优化调度策略

传统的对生产调度的研究是在以下假设条件下进行的:①被调度的工件集合是确定的;②工件的加工时间是确定的,并且在安排计划时全部工件都已到达;③加工工件的机器是连续可用的。这类调度问题是静态调度问题,但实际生产中的大量问题是随机发生的。如在该船厂的管子加工车间中,由于紧急任务的加工托盘插入、加工机器出现故障等随机事件,使得预调度不能正常执行,这就需要安排重调度。这类问题是动态环境下生产调度问题。

针对管子加工车间实际的生产情况和要求,本文制定了在静态调度的基础上,在不确定性和突发性情况下运用动态调度技术对管子加工车间的生产进行动态调度,构建实时反馈柔性调度模型,采用基于多种群混合遗传算法的周期调度策略,把动态连续的问题变成分块的静态问题,从而使复杂问题简单化,动态问题静态化,以保证生产的顺利进行。具体操作流程如图1所示。

由图1可知,实时反馈调度模型在得到资源重组技术对安装托盘生成代加工管的制造托盘信息后,参考安装托盘的开始加工和交货时间以及车间加工资源重组等的目标信息,运用基于混合遗传算法的周期调度方案,得到制造托盘和车间生产计划。此时,系统判断是否有突发事情发生,如有设备故障、负荷不均匀及订单加入等突发事件发生时则使用调度规则算法优化重调度,将各种加工设备和被加工资料的重组信息重新处理,生成新的调度计划和任务,保证生产的顺利进行。如果没有突发事件的发生则按照原来的静态调度的计划进行即可。

图1 实时反馈柔性计划调度操作流程Fig.1 The operation flow of real-time feedback flexible schedule

故该生产调度系统具有能在线产生实时调度、对随机扰动实现在线辨识以及快速进行自动重调度等特点。

2 静态调度问题描述

车间调度问题是一个NP难题,单纯使用某一种优化算法来解决作业车间柔性调度问题时都有一定的局限性。遗传算法(GA)具有很强的全局寻优能力,但求精确解效率低,局部有很强的全局寻优能力,但求精确解效率低,局部搜索能力差。粒子群优化算法(PSO)计算简单、精度高、局部搜索能力强,收敛速度较快,但PSO的全局搜索能力不如GA。根据文献[4-8],本文在研究了GA和PSO基本原理的基础上,综合GA的全局优化能力和PSO的局部寻优能力,提出一种多种群混合遗传粒子群算法,实现在某船厂管子加工车间柔性生产实时调度。

本算法运行时,首先随机产生多个初始解,建立遗传算法初始种群,计算种群中所有个体的适应度进行个体评价,然后进行遗传算子迭代:选择、交叉、变异,利用GA算法进行全局搜索。然后选择遗传算法中最好的PS个个体作为粒子群算法的初始粒子,并将这些初始粒子随机组成PN个粒子群,通过设置不同级别的惯性因子,使各粒子群搜索或侧重于整体搜索或侧重于局部开发,利用粒子群算法计算简单、效率高的特点,快速全面地搜寻出较优良的个体。各粒子群之间亦实行个体迁移,以扩大搜索领域。

结合管子加工车间生产的实际情况,对于实时反馈柔性调度系统在静态或动态条件下的优化实时调度问题描述如下:假设n种规格管子在m台弯管机床上加工,每种规格的管子j由nj根管子组成。为使问题简化,利用成组技术,要求同规格管子之间有工艺上的先后约束,并假定每根管子可由多台弯管机加工,不同规格管子在加工工艺上没有先后约束,每台弯管机在同一时刻只能加工1根管子,在0时刻所有的管子都可被加工,每根管子的加工时间是确定的,工件的装卸时间计算在加工时间内。

本文从管子加工车间的实际要求出发,要求调度结果在满足一定约束的条件下,确定与各设备上所有管子的加工开始时间、完成时间和加工次序,使生产周期(T)、生产成本(C)、设备利用率 (L,B)等加工性能指标达到最优或次优。

3 基于混合遗传算法的优化调度结构

基于上述分析,具有粒子群搜索的多种群混合遗传算法调度流程如图2所示。

1)编码。本文根据简单原则以每根管子作为调度编码基本单元,这样便于使每一个个体都对应一个合法、可行的调度。

2)参数初始化,建立遗传算法初始种群。确定种群规模、交叉概率、变异概率、进化代数等。

3)个体解码。

4)产生权重,计算适应度。权重系数在一定范围内随机产生。由于时间、成本、设备利用率等是不同量纲的参数,可能使得适应度函数变复杂,所以处理多目标问题时,通常采用目标加权法,构建适应度函数,将多目标优化问题转化成单目标优化问题[9]。

适应度函数如下:

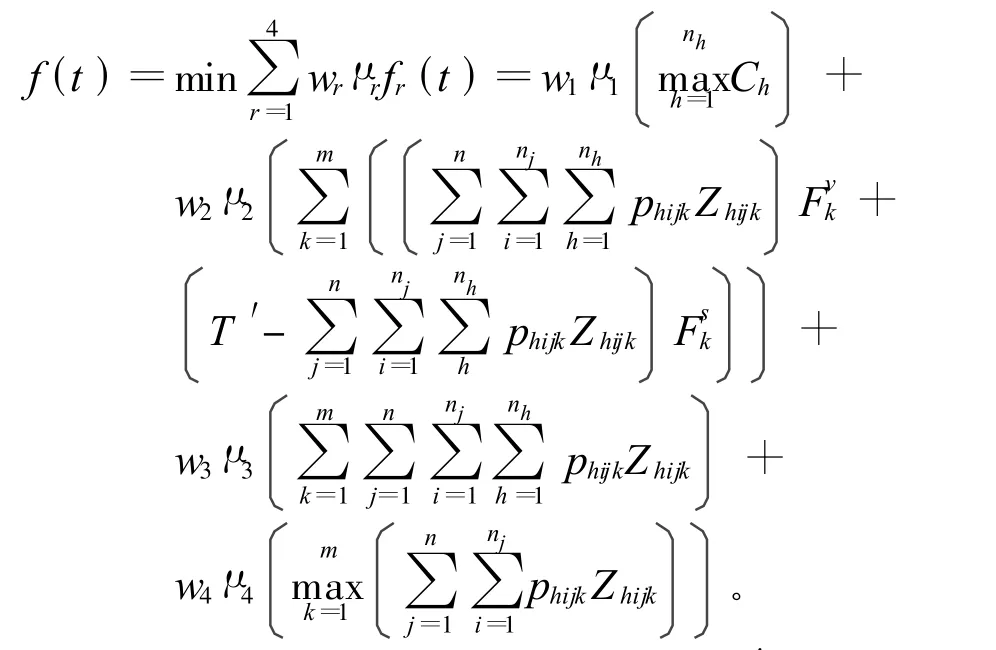
图2 混合算法流程Fig.2 The flow of combining algorithms

式中:Ch为第h类管子的完成时间;T′为该调度方案的最大完成时间;phijk为第h类管子中的第j根管子的第i个工序在第k个机器上加工需要的时间;Zhijk为决策变量,表示第h类管子中的第j根管子的第i个工序是否选择在k机器上加工,Zhijk=1表示选中,Zhijk=0表示未选中为第k个机器实际加工时的机器损耗、人工和加工费用为第k个机器的等待加工时的机器损耗和人工费用;μ1,μ2,μ3,μ4分别为时间、成本、总负荷、最大负荷的量纲统一化系数[9];w1,w2,w3,w4为权系数,且w1+w2+w3+w4=1。

5)判断是否满足条件。是,则转7);否则转5)。

6)遗传进化、个体迁移与替代。按照设定的选择方式进行选择操作,从种群中选出P个染色体个体作为父代染色体个体Pop(t)←selection[G(t)];按交叉概率Pc对染色体个体进行交叉操作(t)←crossover[Pop(t)];按变异概率Pm对染色体个体进行变异操作(t)←mutation[(t)]。在此过程中采用小生境技术以维持种群的多样性、精英选择策略以保证算法的收敛性。

7)粒子群搜索、个体迁移与替代。在粒子群优化算法中,每个优化问题的解称之为“粒子”,在每一次迭代中,粒子通过跟踪2个“极值”来更新自己,粒子本身所找到的最优解,称作个体极值pbest;整个种群当前找到的最优解称作全局极值gbest。每个粒子根据如下的公式来更新自己的速度和位置:

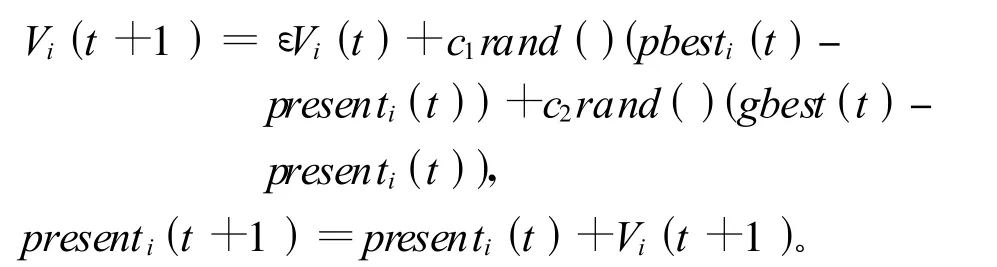
其中:V(t)为粒子的速度;present(t)为当前粒子的位置;c1和c2为正常数,称为加速因子;rand()为[0,1]之间的随机数;ε为惯性因子。

遗传算法搜索完成后,从当前群体中选取最好的PS个个体作为粒子群优化的初始粒子,并组成PN个粒子群,取粒子群中的最优个体作为全局极值gbest,并根据粒子群中各个粒子与全局极值的差异来确定各个粒子的初始速度。然后再利用粒子群算法进行局部搜索,以加快算法后期的收敛速度。根据适应度,各粒子群进行粒子个体迁移与替代。

8)判断是否满足终止条件。如果满足则输出Pareto最优解集;否则转步骤7),继续搜索。

4 仿真与应用结果分析

4.1 仿真试验分析

根据文献[10]中提出的具有15个工件、10台机器、56道工序的大规模柔性调度问题,对本文优化算法与文献[10]中运用的AL+CGA及PSO+SA算法就生产周期、机器总负荷以及关键机器负荷三目标优化调度问题进行了仿真试验,比较结果如表1所示,从而验证了本算法的有效与可行性。

表1 柔性调度15×10问题结果比较Tab.1 Comparing with 15×10 flexible scheduling data

4.2 应用结果分析

某船厂管子加工车间有6台数控弯管机,对5种规格的管子进行生产,每种规格的管子批量为4根,不同规格的管子加工工序不同。由于弯管机的加工范围各不相同,所以每种规格的管子只能在其中的几台设备上加工。对该车间原始生产数据经过处理,得到如表2所示不同种类管子在相关设备上的加工时间,该加工时间包括设备调整和工件安装时间。

机床工时费及工人小时工资费如表3所示,对生产周期、生产成本、机器的总负荷和最大负荷4个性能指标进行优化,循环10次,根据不同权系数得到多个Pareto最优解,如表4所示为部分最优解。限于篇幅,本文仅在图3中输出1例权系数(w1=0.069,w2=0.310,w3=0.071,w4=0.550)的调度甘特图,甘特图中方框内的数字编号表示管子加工工序,如“312”表示第3类管子的第1根在进行第2道工序加工。

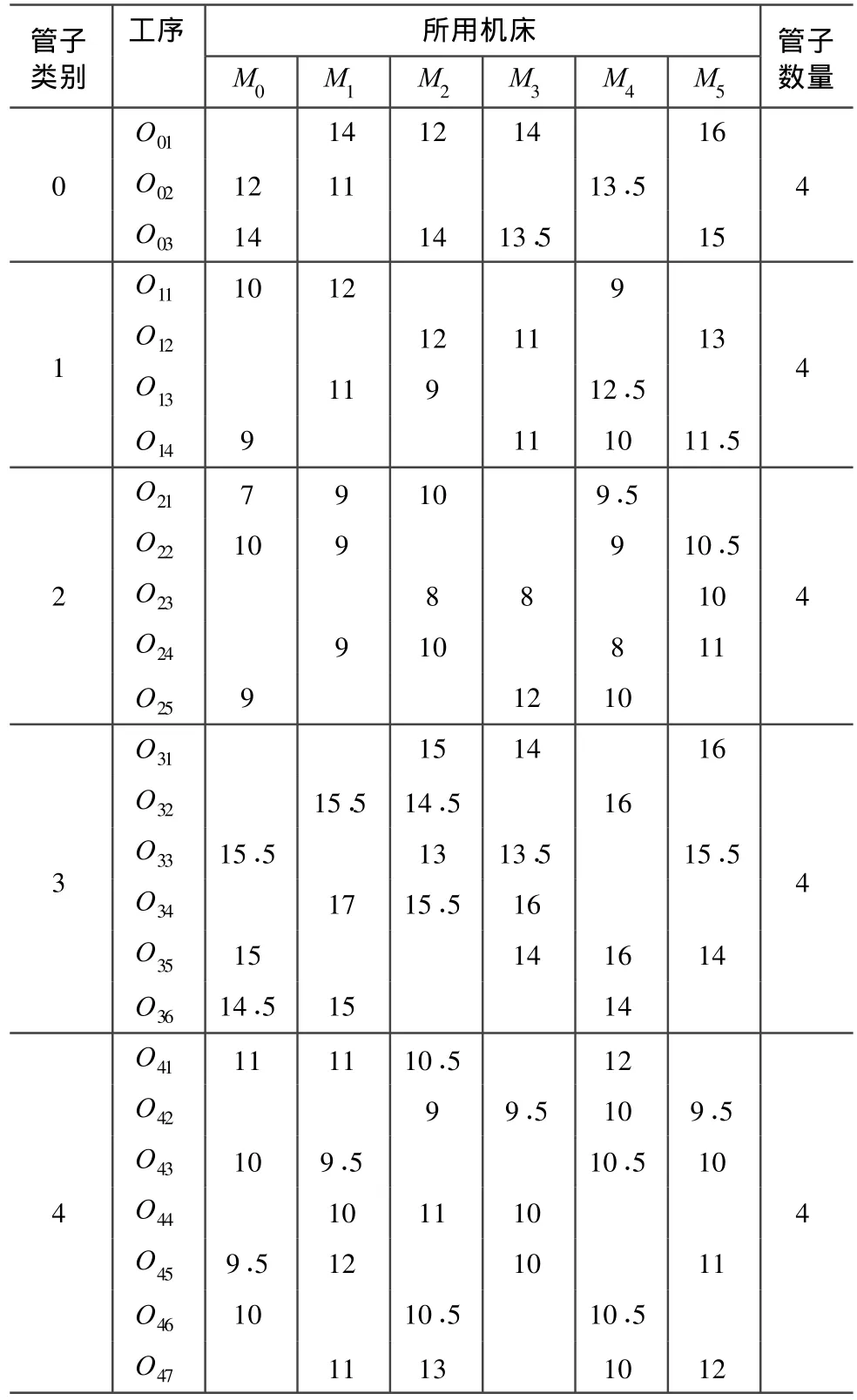
表2 管子加工时间原始数据Tab.2 Original data of piping machining time min

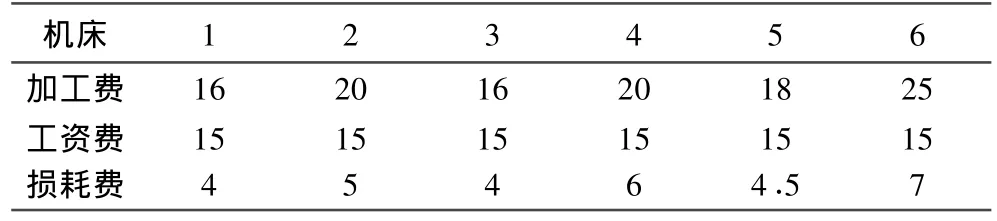
表3 机床工时费及工人小时工资费Tab.3 Expense of machines and operators Yuan/h

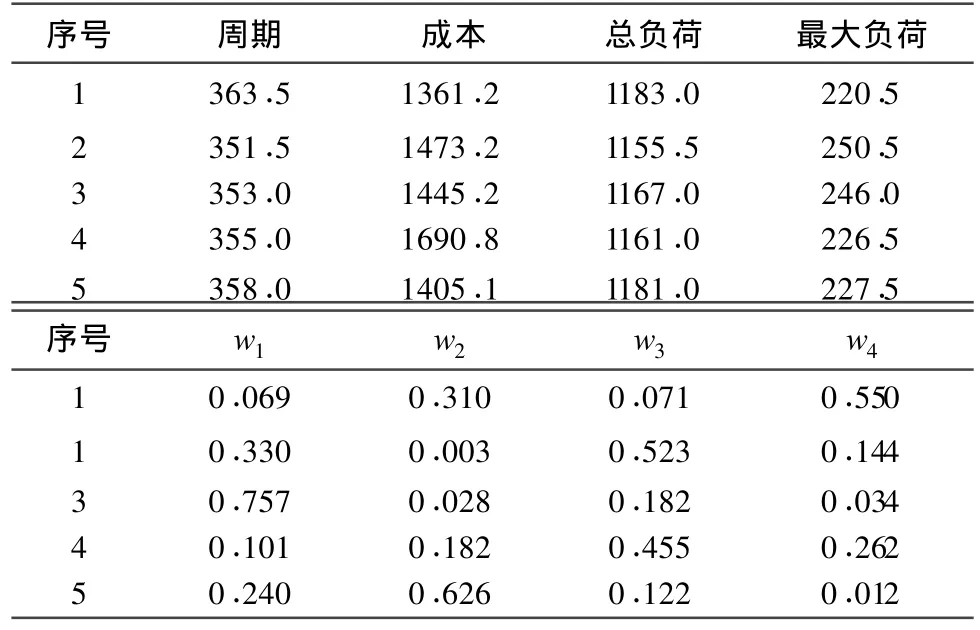
表4 不同权系数下的部分最优解Tab.4 Member of pareto data

图3 权系数为(w1=0.069,w2=0.310,w3=0.071,w4=0.550)的调度甘特图Fig.3 The gunter chart of real-time flexible scheduling

基于多种群混合遗传算法的车间实时柔性优化调度系统在某船厂管子加工车间的应用取得了很好的效果,生产成本大幅降低,生产效率相比应用本调度系统之前提高了近1.5倍。同时由于在本调度系统中组合实时反馈调度模型,使得车间具备处理突发事件的能力,车间生产线具有高度的柔性。

5 结 语

针对传统车间调度问题的局限性,本文结合生产实际情况,对生产中出现机器故障或紧急任务突然加入等突发事件的调度问题展开研究,并考虑现代生产敏捷制造的要求,建立了基于多种群混合遗传粒子群算法的车间实时调度系统。该系统在静态调度的基础上,通过构建实时反馈柔性调度模型,在不确定性或突发性事故出现的情况下运用动态调度技术对车间的生产进行调度,把动态连续的问题变成分块的静态问题,从而使动态问题静态化,形成了实时调度的柔性计划调度技术。

利用遗传算法和粒子群算法的优点,通过多种群搜索将GA和PSO两种算法结合到一起,可取长补短。遗传算法是从维护种群多样性的角度来避免早熟收敛,粒子群算法则是从避免传统遗传算法变异算子的随机性和盲目性的角度提高收敛效率,使优化效果更加理想。仿真及实际生产应用结果表明了该模型及算法的有效和合理性,具有一定的理论和实践意义。

[1] 何霆,刘飞,等.车间生产调度问题研究[J].机械工程学报,2000,36(5):97-102.

HE Ting,LIU Fei,et al.Research on workshop producing scheduling problems[J].Chinese Journal of Mechanical Engineering,2000,36(5):97-102.

[2] HALL N G,SRISKANDARAJAH C.A Survey of machine scheduling problems with blocking and no-wait in process[J].Operations Research,2005,44(3):510-525.

[3] 唐立新.CIMS下生产批量计划理论及其应用[M].北京:科学出版社,1999.

TANG LI-xin.The theory and application ofbatch producing scheme base on CIMS[M].Beijing:China Science Press,1999.

[4] KONAK A,COIT D,SMITH A.Multi-objective optimization using genetic algorithm:a tutorial[J].Reliability Engineering and System Safety,2006,91(9):992-1007.

[5] CARLOS A,GREGORIO T,MAXIMINO S.Handing multiple objectives with particle swarm optimization[J].IEEE Transactions on Evolutionary Computation,2004,8(3):256-279.

[6] SAKAWA M,KUBOTA R.Fuzzy programming for multiobjective job-shop scheduling with fuzzy processing time and fuzzy due date through genetic algorithm[J].European Journal of Operational Research,2000,12(2):393-407.

[7] TADAHIKO M,ISHIBUCHI H,HIDEO T.Multi-objective genetic algorithm and its application to flow shop scheduling[J].Computers and Engineering,1996,30(4):957-968.

[8] ALLAHVERDI A,ALDOWAISAN T.New heuristics formmachine no-wait flow shop to minimize total completion time[J].The International Journal of Management Science,2004,(32):345-352.

[9] 王凌.车间调度及其遗传算法[M].北京:清华大学出版社,2003.

WANG Ling.Research on workshop scheduling problems and genetic algorithm[M].Beijing:Tsinghua University Press,2003.

[10]KACEM I,HAMMADIS,BORNE P.Pareto-optimality approach for flexible job scheduling problems:hybridization of evolutionary algorithms and fuzzy logic[J].Mathematics and Computers in Simulation,2002,60(3-5):245-276.

Real-time flow-shop scheduling system based on multi-population hybridization of genetic algorithm and particle swarm optimization

CHENG Guo-huang1,XIA Shen-xiong1,WANG Yu1,2,YAN Rui1
(1.Wuchang Shipbuilding Industry Co.,Ltd,Wuhan 430060,China;2.Huazhong University of Science and Technology,Wuhan 430074,China)

Flexible flow-shop scheduling problem is a non-polynomial problem.To solve several problems of a pipe-curving workshop in this article such as underproduction,disordered production management and improved efficiency,the real-time feedback adjustment scheduling model and the real-time job-shop scheduling system based on multi-particle swarm optimization hybrid genetic algorithm are given by the dynamic flexible scheduling technology.Through the scheduling model and scheduling system,the dynamic sequential flow-shop scheduling problem is become a static blocking scheduling problem.The performance of the model and system are evaluated and compared with those of other representative approaches through simulations and practiced applications,and the results demonstrate the feasibility,rationalization and efficiency of the real-time scheduling system.

genetic algorithm(GA);particle swarm optimization(PSO);flow-shop scheduling;realtime scheduling system

TP18

A

1672-7649(2011)11-0126-05

10.3404/j.issn.1672-7649.2011.11.030

2010-12-06;

2011-02-22

湖北省科技厅科技攻关计划资助项目(2007AA109A01);武汉市科技局科技成果推广应用计划研究资助项目(200731414455)

成国煌(1976-),男,硕士,工程师,从事设计及系统开发工作。