基于Simulink的飞航式火箭助飞鱼雷空中弹道仿真
2011-07-11曲延明林宗祥
曲延明,周 明,林宗祥
(1.海军大连舰艇学院研究生管理大队,辽宁 大连 116018;2.海军大连舰艇学院 装备自动化系,辽宁 大连 116018)
基于Simulink的飞航式火箭助飞鱼雷空中弹道仿真
曲延明1,周 明2,林宗祥1
(1.海军大连舰艇学院研究生管理大队,辽宁 大连 116018;2.海军大连舰艇学院 装备自动化系,辽宁 大连 116018)
为研究飞航式火箭助飞鱼雷空中弹道参数设计问题,首先分析其空中运动过程,根据空中弹道的特点,建立了纵向运动方程组。采用MATLAB/Simulink软件建立了仿真模型,并就发射倾角、雷箭分离条件等对空中弹道的影响进行仿真计算。本文的研究成果对飞航式火箭助飞鱼雷空中弹道设计及作战效能研究有一定的参考价值。
飞航式火箭助飞鱼雷;空中弹道;仿真
0 引言
飞航式火箭助飞鱼雷是采用“飞航导弹+鱼雷”的技术,利用火箭助推器使战斗部(鱼雷)在空中高速飞行,当到达目标区域时,雷箭分离,鱼雷入水攻击目标。在研究飞航式火箭助飞鱼雷的作战效能等问题时,其空中弹道的仿真模型是关键因素之一。
飞航式火箭助飞鱼雷的空中弹道可用1组复杂的微分方程描述,该方程组无法直接求得解析解,必须借助现代仿真技术。本文采用MATLAB/Simulink软件进行仿真建模,结构清晰,易于调试。通过仿真计算,分析了发射倾角、雷箭分离条件等对空中弹道的影响;参考“米拉斯”反潜导弹的弹道性能设定参数,得到了射程与飞行时间的关系。文中的研究成果为飞航式火箭助飞鱼雷的弹道设计及作战效能研究提供有益参考。
1 弹道概述
飞航式火箭助飞鱼雷的空中弹道可分为助飞弹道和雷箭分离后的雷伞弹道2部分。其中,助飞弹道从发射到雷箭分离点止,分为助推段、调整段和巡航平飞段。如图1所示,WA为助推段,AB为调整段,BC为巡航平飞段,CD为雷伞段[1]。

图1 空中弹道示意图Fig.1 Schematic of air trajectory
飞航式火箭助飞鱼雷发射出箱后,在助推器的作用下开始爬升,达到预定高度与速度后,助推器脱落,助推段结束。涡喷发动机点火,控制系统根据无线电高度表调整鱼雷爬升或降高,使达到巡航高度。在巡航平飞过程中可通过无线电指令修正系统对雷箭分离点进行修正。到达雷箭分离点时,发动机自动关闭并与鱼雷分离。雷箭分离后,降落伞打开,鱼雷减速下降、入水。入水后,下潜至预定搜索深度,按照设定的方式搜索和攻击目标。
2 数学模型
完整的空中弹道分析应在地面、速度、雷体等几个坐标系确定的三维空间中进行,涉及到的方程及参数众多。本文研究关心的是射程、巡航高度和飞行时间,因此将空中弹道方程组简化,令各侧向运动参数为0,得到飞航式火箭助飞鱼雷的纵向运动方程组。
2.1 助飞弹道模型
把飞航式火箭助飞鱼雷简化为质点,即不考虑其运动过程中的转动问题,则助飞弹道的运动方程组可简化为[2]:
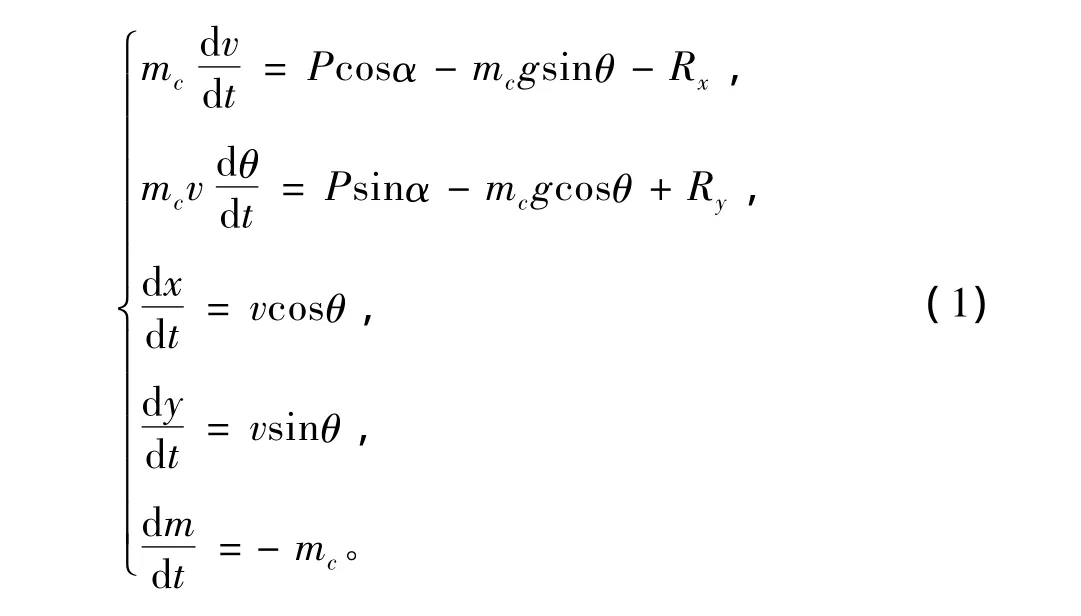
方程中所含未知量为:射程x、射高y、速度v、弹道倾角θ、鱼雷瞬时质量mc。式中所含已知参数有:攻角α,助推器推力P,空气阻力Rx,空气升力Ry,重力加速度g。对以下几个参数进行解算。
1)空气阻力Rx
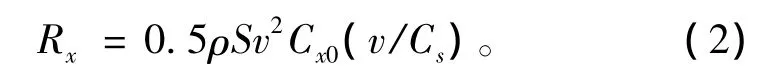
式中:ρ为空气密度,与高度有关,由于助飞鱼雷平飞高度较低,可取地面标准值1.205 74 kg/m3;S为鱼雷截面积,是鱼雷弹径d的函数,S=0.25πd2;Cs为声速;Cx0为攻角为0时的阻力系数。
2)空气升力Ry

在助飞段不考虑由角速度引起的升力,则

式中:Cy为升力系数;为气动参数。
2.2 雷伞弹道模型
雷箭分离是1个复杂的过程,本部分只分析雷箭分离后的雷伞段弹道。为方便计算,对于稳定性较好的降落伞,可以近似认为伞的迎面阻力方向与雷伞连接点E处的方向一致,从而可以直接求出伞对雷的作用力FE的大小与方向,无须联立求解有关伞的运动方程组。由此建立如图2所示坐标系[3]。

图2 雷伞系统坐标系Fig.2 Torpedo-umbrella system coordinates
E点处的速度vE的大小与方向为:FE的大小与方向为:

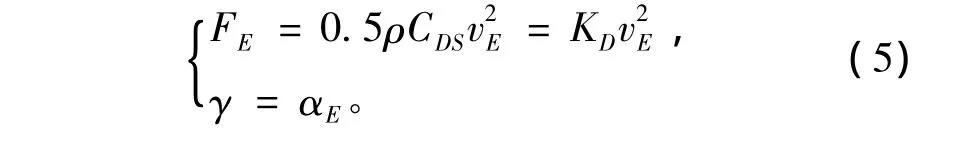

于是由方程组可解出雷伞系统纵向运动的弹道参数及入水时鱼雷各运动参数。
方程中所含未知量有射程x0,射高y0,速度v,攻角α,俯仰角ϑ,弹道倾角θ,鱼雷俯仰角速度ωz。
方程中所含已知参数有雷伞段鱼雷质量m2,空气阻力Rx,空气升力Ry,开伞载荷系数KD,鱼雷质心至E点的距离LCE,FE与x轴夹角γ,转动惯量Jzz,纵轴力矩MZ。其中,

3 仿真建模
根据方程组(1)建立如图3所示的助飞弹道的Simulink模型;根据方程组(6)建立如图4所示的雷伞弹道的 Simulink 模型[4]。

图4中包含的Out_V模块、Out_Seita模块和Out_W模块的仿真模型分别如图5~图7所示。

4 仿真结果与分析
4.1 发射倾角对初始弹道的影响
将助推段时间设定为6 s,调整段时间设定为3 s,攻角设定为 10°,分别计算发射倾角为 15°,30°,45°时的初始弹道与速度曲线。
如图8所示,弹道倾角越大,飞航式火箭助飞鱼雷到达的平飞高度越高,且水平飞行的距离越近。如图9所示,发射倾角越大,初始段所达到的速度越小,但发射倾角对速度的影响并不是非常明显。当发射倾角从15°增加到45°时,火箭助飞鱼雷的速度由253 m/s降至222 m/s。因此,可以通过适当增加发射倾角使火箭助飞鱼雷尽快到达预定的飞行高度,而对飞行速度影响不会太大。
4.2 雷箭分离条件对雷伞弹道的影响
图10给出了雷箭分离速度为0.7Ma,开伞载荷系数KD为0.9,分离高度为300 m,250 m,200 m时的雷伞段弹道。计算结果表明,分离高度越高,水平飞行距离越远。当分离高度从200 m增加到300 m时,入水点的水平距离增加了约250 m。

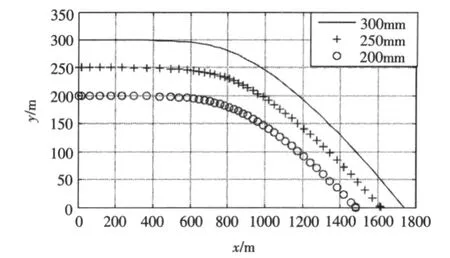
图10 不同分离高度时的雷伞段弹道Fig.10 Torpedo-umbrella trajectory in different altitude
图11给出了雷箭分离高度为300 m,开伞载荷系数KD为0.9,分离速度为0.7Ma,0.8Ma,0.9Ma时的雷伞段弹道。计算结果表明,分离速度对水平飞行距离的影响不明显。当分离速度从0.7Ma增加到0.9Ma时,入水点的水平距离仅增加了约70 m。

图12给出了分离高度为300 m,分离速度为0.75Ma,攻角为 0°,分离姿态角分别为 0°,-5°和-10°的雷伞段弹道。计算结果表明,分离姿态角对雷伞段弹道有较大影响,当分离姿态角为-10°时,雷伞系统迅速下降;当分离姿态角为0°时,雷伞系统平飞约400 m才开始下降,且入水点距离增加了约500 m;分离姿态角对入水角影响不大,计算获得的入水角分别为 -20.6°,-18.9°,-18°。图13给出了分离姿态角分别为0°,-5°,-10°时的速度曲线(参数设定同上)。由图可知,分离姿态角对速度影响不是很大,前10 s速度下降均很快,从255 m/s下降到30 m/s,之后速度基本稳定在30 m/s左右直至入水。另外,可以看出姿态角越大,雷伞系统滞空时间越短,分别为62 s,49 s,35 s。
4.3 射程与飞行时间的关系
空中弹道确定后,可以很容易地得到射程与飞行时间的关系。根据4.1节和4.2节的仿真分析,并参考“米拉斯”反潜导弹的弹道性能,设计1个简单的纵向弹道模型,参数设定如下:发射倾角15°,助推器工作时间6 s,巡航高度300 m,巡航速度0.75Ma,分离姿态角-10°。
通过仿真计算,可得到射程与飞行时间的关系式如下:

5 结语
1)本文利用MATLAB/Simulink对飞航式火箭助飞鱼雷空中弹道进行仿真建模,具有建模速度快、代码编写少、易于调试等优点,并且所获得的仿真结果是合理的。
2)由计算结果可知,发射倾角对助飞弹道有较大影响;雷箭分离条件,如分离姿态、高度对雷伞弹道有较大影响,分离速度对雷伞弹道影响不大。
3)在对飞航式火箭助飞鱼雷进行作战效能分析时,引入本文的空中弹道仿真模型,可找出各参量对鱼雷作战效能模型输出数据的影响,可以有效地提高鱼雷作战效能。
[1]傅英,等.国外海军鱼雷装备[M].北京:海潮出版社,2007.210 -212.
[2]徐明友.火箭外弹道学[M].哈尔滨:哈尔滨工业大学出版社,2004.21 -25.
[3]张宇文.鱼雷弹道与弹道设计[M].西安:西北工业出版社,1999.264 -266.
[4]毕开波,等.飞行器制导与控制及其MATLAB仿真技术[M].北京:国防工业出版社,2009.190-198.
Research on air trajectory simulation of the cruising rocket assisted torpedo based on simulink
QU Yan-ming1,ZHOU Ming2,LIN Zong-xiang1
(1.Postgraduate Administer Team of Dalian Naval Academy,Dalian 116018,China;2.Department of Equipment and Automatization,Dalian Naval Academy,Dalian 116018,China)
To research the issue of designing air trajectory parameter of the cruising rocket assisted torpedo,the paper analyzed its movement process in the air,and constructed the equational group of lengthways movement according to its air trajectory,and set up the simulation model based on MATLAB/Simulink,and calculated the influence aroused by some factors such as firing angle and the separate condition of torpedo and rocket.The conclusion of the paper has a certain extent meaning to the ballistic design and operational effectiveness of cruising rocket assisted torpedo.
cruising rocket assisted torpedo;air trajectory;simulation
TJ761.5;TJ63+1
A
1672-7649(2011)12-0107-05
10.3404/j.issn.1672-7649.2011.12.026
2011-03-22;
2011-07-18
曲延明(1982-),男,硕士研究生,研究方向为鱼雷武器作战使用。
