奇异值分解算法在舰船腐蚀相关电场建模中的应用

岳瑞永

(水下测控技术重点实验室，辽宁 大连 116013)

奇异值分解算法在舰船腐蚀相关电场建模中的应用

岳瑞永

(水下测控技术重点实验室，辽宁 大连 116013)

基于线性反演理论，讨论了舰船腐蚀相关电场电偶极子模型的稳定性问题，在此基础上将奇异值分解算法应用于建模，通过摒弃模型矩阵方程核矩阵的小奇异值，来改善核矩阵的病态程度，提高数据方程反演的稳定性。数值试验表明，当反演数据存在一定误差时，奇异值分解算法相对于最小二乘算法可以明显降低数据误差引起的模型参数扰动，有效地提高模型的稳定性。实船实测数据建模结果进一步验证了奇异值分解算法提高模型稳定性的有效性。

奇异值分解;腐蚀相关电场;建模

0 引言

本文首先介绍了舰船腐蚀相关电场电偶极子建模基本理论，然后分析了影响模型稳定性的主要因素，在此基础上将广义逆反演用于建模逆问题求解，利用奇异值分解算法提高求解的稳定性，通过数值试验验证了奇异值分解算法提高模型稳定性的有效性。最终利用上述方法对某船实船腐蚀相关电场进行了建模和预测。

1 舰船腐蚀相关电场建模基本理论

舰船腐蚀相关电场偶极子建模方法与磁场建模方法原理基本一致，是基于惟一性定理，利用布置于船体上一系列电偶极子产生水下电场的叠加来拟合舰船实际水下电场［3］。通常偶极子以均匀间距布置在舰船首尾中心线上或两侧。为了便于描述舰船腐蚀相关电场，规定如下坐标系，xoy平面与空气—海水界面重合，x轴平行于舰船首尾中心线方向，指向船首为正，称为纵向;y轴垂直于首尾中心线方向，以指向右弦为正;z轴垂直于海平面，以向下为正，称为垂直方向。下面介绍舰船水平电偶极子阵列模型的构建方法。

假设在舰船水下部分布放n个x方向水平电偶极子，其坐标分别为 (x'j，y'j，z'j)，电偶矩分别为Pxj，则每个水平电偶极子在海水中点Si(xi，yi，zi)产生的电场为:

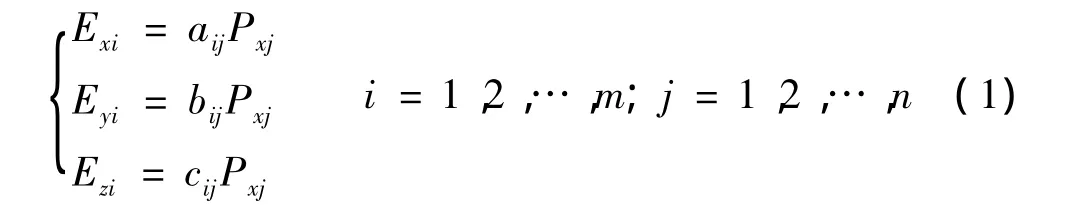
其中:m为测点个数;aij，bij，cij分别为单位电偶矩的第j个水平电偶极子在第i个测点Si(xi，yi，zi)产生的电场纵向分量、横向分量和垂直分量。

将线性方程组(1)写成矩阵形式:

令M=3m，N=n，则d为M×1维向量，称为观测数据向量;G为M×N阶矩阵，称为数据核矩阵;m为N×1维向量，称为模型参数向量。

式(2)是舰船腐蚀相关电场电偶极子模型的矩阵方程，由矩阵代数便可求出式(2)的解。由于舰船腐蚀相关电场建模中，观测数据向量的长度通常大于模型向量长度，因此式(2)一般为超定方程，存在最小二乘解:

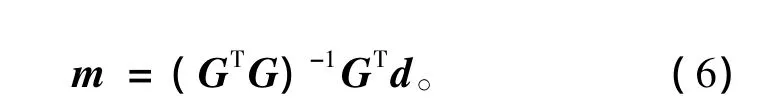
由式(6)计算偶极子电偶矩后，便可利用式(1)计算其他测点的舰船腐蚀相关电场值，实现测量数据的深度和距离换算。

概率统计是大学本科开设的一门主要的基础学科，它来源与实际生活，现实生活中的许多问题都要用它来就解决。概率统计在自然科学,社会科学,工农业生产，金融，经济方面有这广泛的应用。而目前许多的概率统计教材都普遍侧重理论而轻视应用，从某种程度上而言，概率统计的教学成了高等数学的教学，而忽视了这一学科本身特有的思想方法，造成同学们改到难学，乏味，无趣，直至厌学。针对这种情况，本人结合自己在教学中的体会，对概率统计教学进行了一些探索。取得了较好的结果。

2 舰船腐蚀相关电场建模稳定性讨论

由式(2)可知，舰船腐蚀相关电场电偶极子建模在本质上属于线性反演问题，也就是从数据空间到模型空间的映射问题。根据反演理论，如果数据空间存在1个小范围变换，相应于模型空间存在1个大范围的变化，则称这种映射是不稳定的［4］。因此选用合适的线性反演方法对提高模型的稳定性显得非常重要。

线性方程(2)解的稳定性由数据核矩阵G的性质决定。当G条件数较小，式(2)是良态的。G的条件数越大，数据方程的病态程度愈严重。L2范数意义下，G条件数定义如下:

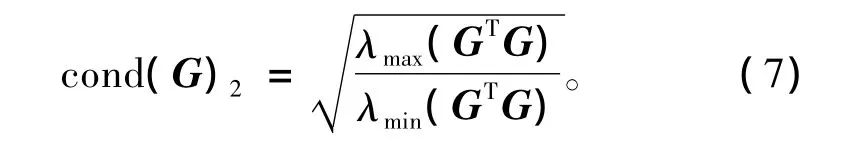
式中:λmax(GTG)为GTG的最大特征值;λmin(GTG)为GTG的最小特征值。

由式(7)可知，如果矩阵GTG的秩r＜N，即GTG存在零特征值，则G的条件数为无穷大，数据方程是奇异的，无法求解。如果GTG非奇异，但是存在很小的特征值，则G的条件数很大，数据方程是病态的，解存在极大的不稳定性。在构建舰船腐蚀相关电场模型过程中，当模型电偶极子数量较多时，核矩阵G的条件数高达106，核矩阵存在严重的病态性，在这种情况下采用式(6)求解模型向量m存在一定的不稳定性。

3 奇异值分解［4－6］

奇异值分解是线性反演中求解病态或奇异矩阵方程的一种非常有效的方法，基本原理是:如果矩阵G是M×N阶奇异矩阵，则可将其分解为如下形式:

式(8)便为奇异矩阵G的奇异值分解。其中:r为矩阵G的秩，Ur为矩阵GGT之M×r阶特征向量矩阵;Vr为矩阵GTG之N×r阶特征向量矩阵，Λr是由矩阵G的r个奇异值λi组成的对角线矩阵，即:

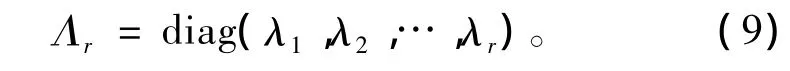
王家映、李平等指出，矩阵G相对大的奇异值对应模型参数中稳定和可靠的成分，而小的奇异值则表示统计上不可靠的成分，小奇异值的存在会使矩阵方程求解变得极不稳定。因此将小的奇异值截取，使数据核矩阵G的条件数得到改善，便可得到方程稳定解:

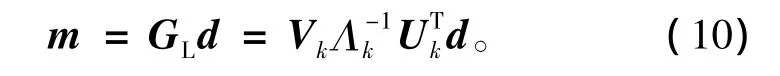
式中:GL为矩阵G的广义逆;Λk为按从大到小顺序保留下的k个奇异值组成的对角线矩阵;Uk和Vk为相对应的特征向量矩阵。

Wiggins建议通过设定1个模型向量方差门限值t，使

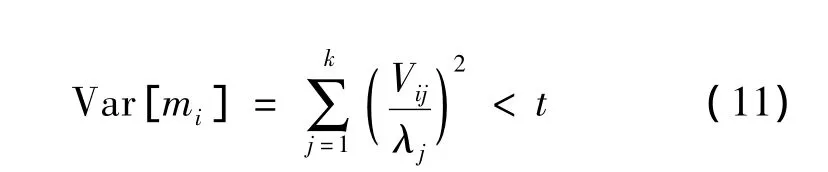
来确定被保留奇异值的个数k，即仅保留k个大奇异值，而截断r－k个小奇异值。

4 数值试验

利用一系列水平电偶极子组合来模拟舰船腐蚀相关电场，偶极子个数共23个，以5 m间距沿舰船首尾中心线均匀布置，偶极子电偶矩通过舰船边界元模型计算数据反演得到。海水深度为30 m，海水电导率3.7 S/m，海床电导率为1.0 S/m。图1是上述模型计算得到的舰船腐蚀相关电场曲线。

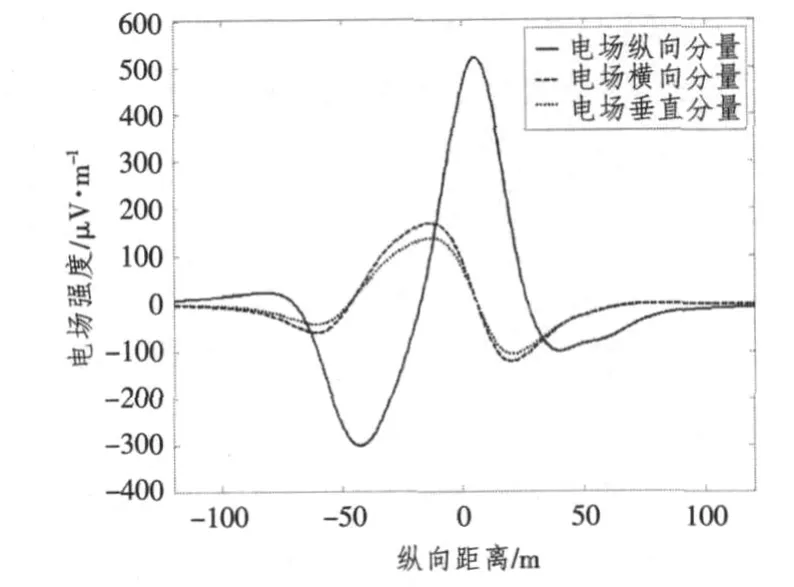
图1 舰船腐蚀相关电场正演理论曲线Fig.1 The forward theoretical data curve of the ship's corrosion related electric field

将正演数据作为实测数据向量，假定水平电偶极子位置和海洋参数均为已知，构建矩阵方程，利用最小二乘法进行求解，反演得到的偶极矩值与理论值完全一致，表明在数据不存在误差情况下采用最小二乘法便可进行精确求解。在正演数据中加入高斯噪声，使数据向量存在误差，分别利用最小二乘法和奇异值分解进行反演，结果如图2所示，其中星线为理论模型，方形线为最小二乘法反演结果，菱形线为利用奇异值分解截取小的奇异值后反演结果。由图2可看出，当数据向量存在误差时，最小二乘法得到的模型与理论模型存在巨大差异，表明该方法的稳定性较差。而奇异值分解结果与真实模型差异相对较小，且变化趋势基本保持一致，表明奇异值分解算法可以有效地抑制误差影响，具有较高的稳定性。

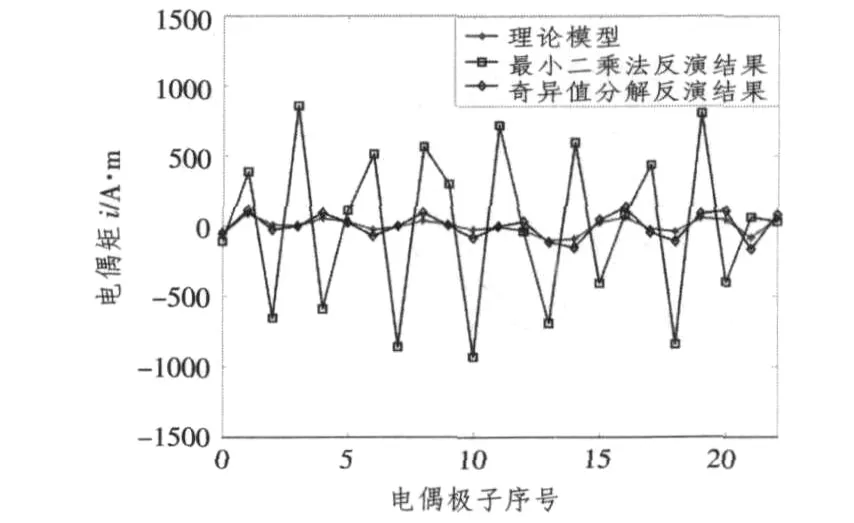
图2 正演理论数据加入高斯噪声的反演结果Fig.2 The inversion results of forward theoretical data adding with Gauss noise

5 舰船实船腐蚀相关电场建模与预测

利用上述方法对某船实船腐蚀电场进行了建模和预测。该船船长28 m，宽5.4 m。所构建的舰船腐蚀相关电场模型由10个水平电偶极子组成，偶极子以均匀间距对称布置在舰船首尾中心线两侧，海水电导率为4.1 S/m，海水深度为13.1 m，测量体水深为12.4 m，海床电导率假定为0.3 S/m。图3是舰船某单程(正横距2 m)腐蚀相关电场建模结果，实线表示实测数据，虚线表示模型理论计算值，从图中可看出测量值和理论计算值吻合的较好。图4是利用另一单程(正横距为40 m)实测数据对所建模型的验证结果，由图中可看出模型正演曲线与实测曲线变化趋势基本一致，表明所构建的数学模型具有一定的精度和稳定性。需要说明的是由于该单程水下电场垂直分量没有明显的通过特性，因此本文未给出垂直分量验证曲线。

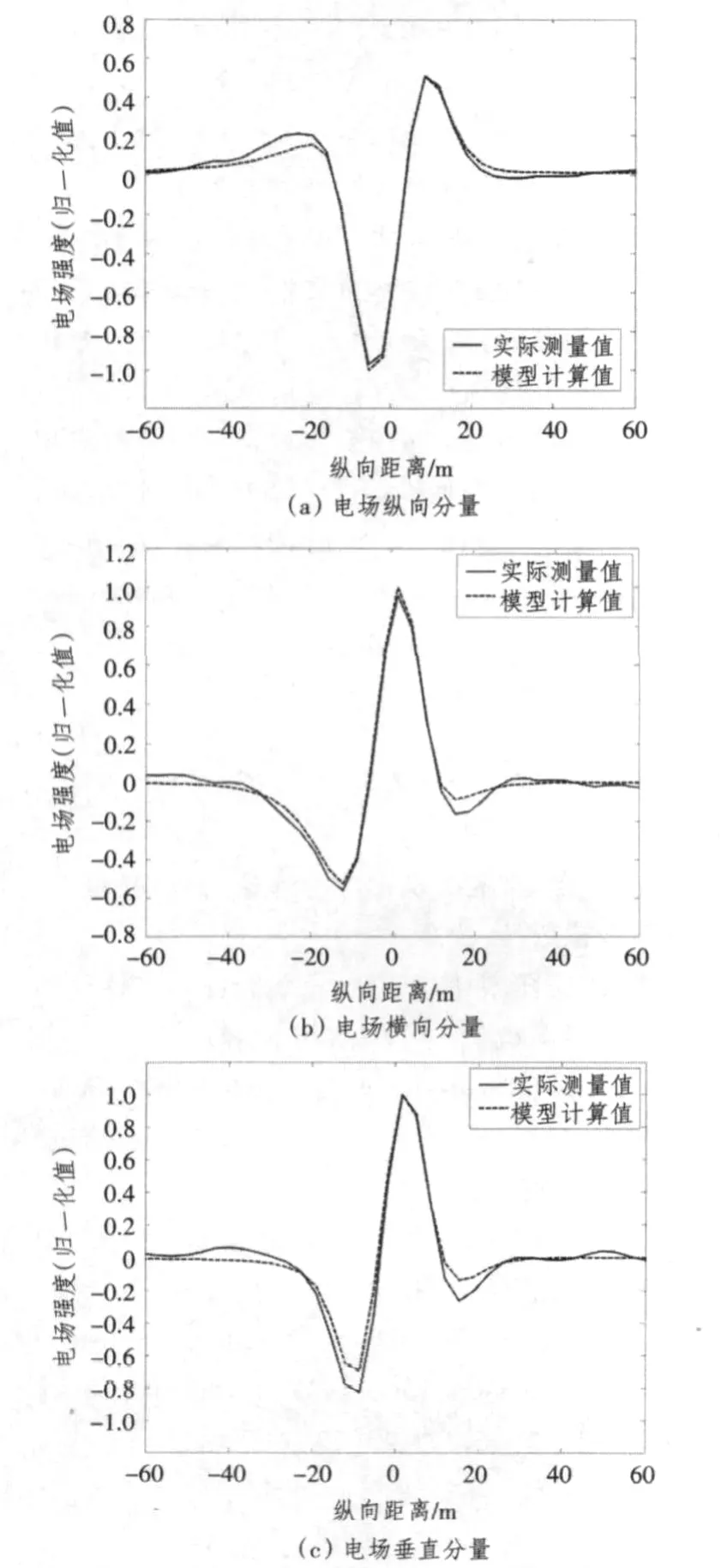
图3 某船腐蚀相关电场建模结果Fig.3 The modeling result of a certain ship's corrosion related electric field

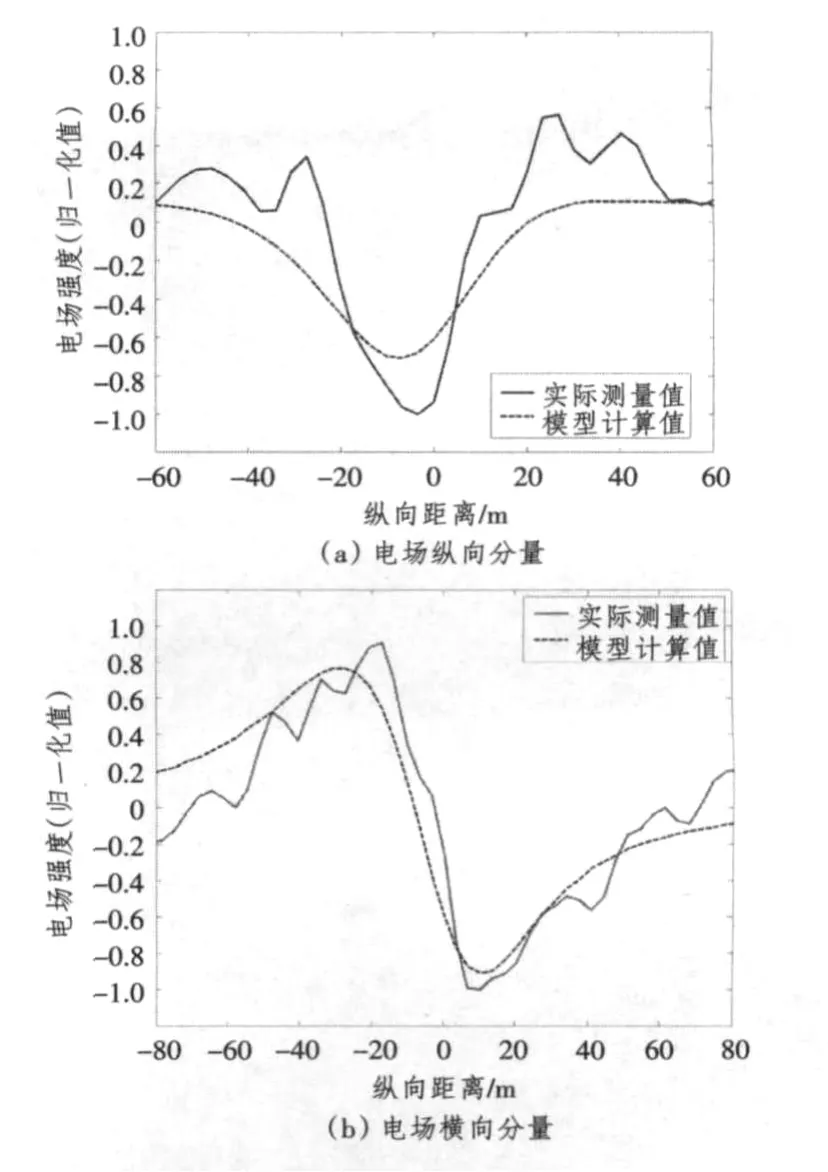
图4 某船腐蚀相关电场验模结果Fig.4 The validation result of a certain ship's corrosion related electric field modeling

图5是利用上面构建的偶极子模型预测得到的目标船腐蚀相关电场在海底大平面分布。由图可发现，该船腐蚀相关电场纵向分量和垂直分量沿舰船首尾中心线对称分布，而横向分量沿舰船首尾中心线反对称分布;电场强度峰值出现在舰船中部，船首和船尾区域;电场强度纵向分量幅值最大，横向分量次之，垂直分量最小;电场强度纵向分量在舰船首尾中心线方向异常范围约为80 m，即3倍船长，在横向异常范围约为80 m，即3倍船长;横向分量在舰船首尾中心线上幅值基本为0，这种现象是由于舰船主要电场源沿舰船首尾中心线对称分布而产生的;电场强度垂直分量异常区域较小，在纵向和横向异常范围均约为1倍船长。

6 结语

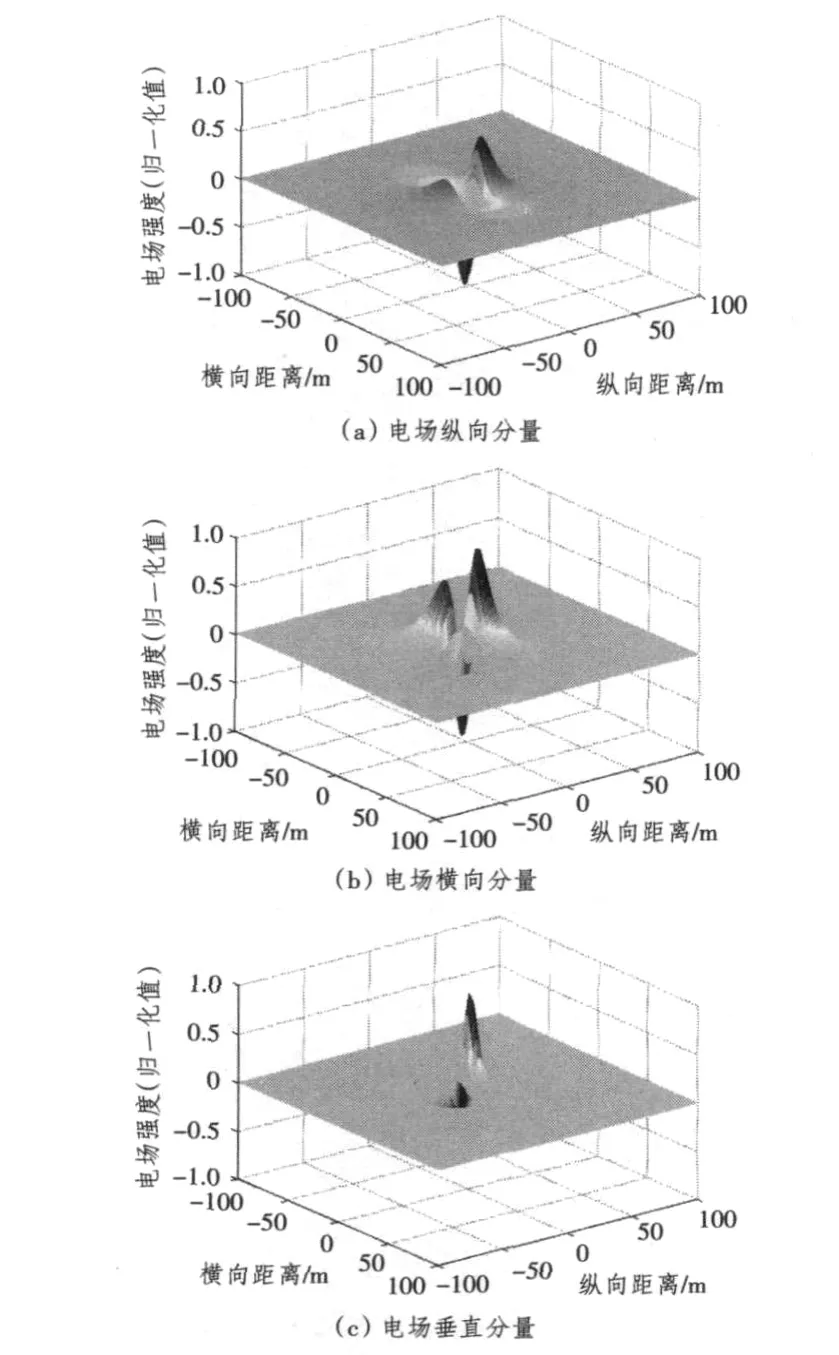
图5 模型预测得到的某船腐蚀相关电场海底大平面分布Fig.5 The ship's corrosion related electric field distribution on the sea bed which is predicted from the electric dipoles modeling

本文从线性反演理论出发研究了舰船腐蚀相关电场电偶极子模型的稳定性问题，发现小的奇异值是造成模型不稳定的重要因素。在此基础上将奇异值分解算法应用于舰船腐蚀相关电场建模，通过截断小的奇异值来提高模型的稳定性。数值试验表明，当反演数据存在一定误差时，奇异值分解算法相对于传统的最小二乘算法可以明显降低数据误差引起的模型参数扰动，能有效地提高模型的稳定性。利用上述方法对某船实船腐蚀相关电场进行建模和预测，发现该船腐蚀相关电场纵向分量和垂直分量沿舰船首尾中心线对称分布，横向分量则沿首尾中心线反对称分布。

［1］DAVIDSON S J，RAWLINS P G.A multi-influence range［C］.Proceeding of the European Conference on Underwater Defence Technology，UDT Europe，1999.169 －173.

［2］HOITHAM P，JEFFERY I，et al.Electromagnetic signature modeling and reduction［C］.Proceeding of the European Conferenceon UnderwaterDefence Technology，UDT Europe，1999.97 －102.

［3］刘胜道，龚沈光.舰船水下静电场的电偶极子模型［A］.水中目标特性研究学术论文集［C］.2002.232－241.

［4］王家映.地球物理反演理论［M］.北京:高等教育出版社，2002.

［5］李平，王椿镛.地球物理反演中奇异值分解应用的若干问题探讨［J］.自然科学进展，2001，11(8):891 －896.

［6］WIGGINS R A.The generalized linear inverse problem:implication of surface waves and free oscillations for earth structure［J］.Review Geophysical Space Physics，1972，(10):215－285.

Application of singular value decomposition(SVD)algorithm in the ship's corrosion related electric field modeling

YUE Rui-yong
(Science and Technology on Underwater Test and Control Laboratory，Dalian 116013，China)

In this paper，the stability of the ship's corrosion related electric field model of the electric dipole array is discussed.The SVD algorithm is applied to the solving process of the model matrix equation.The stability of the model can be increased by cutting off the little singular value of the kernel matrix.The numerical tests show that the turbulence of the model parameters originating from the measured data error can be reduced significantly by use of the SVD algorithm relative to the least-squares method.The modeling results of a certain ship's real data also verify the validity of the SVD algorithm.

singular value decomposition;corrosion related electric field;modeling

U665.26

A

1672－7649(2011)12－0046－05

10.3404/j.issn.1672－7649.2011.12.010

2011－04－12;

2011－05－12

国防基础科研基金资助项目(A0820110019);水下测控技术重点实验室基金资助项目(9140C2604050906)

岳瑞永(1980－)，男，硕士，工程师，研究方向为舰船物理场测试与分析。