钱塘江河口段洪水冲刷效果的影响因素研究

唐子文,陈甫源,梁民阳

(1.浙江省水利河口研究院,浙江 杭州 310020;2.浙江省钱塘江管理局,浙江 杭州 310016)

1 问题的提出

钱塘江河口具有潮大流急、河床冲淤幅度大、变形速度快的特点,杭州段洪水位除了与洪水流量大小直接有关外,还受到江道冲淤面貌(容积大小、沙坎顶点高程及江道平面弯曲程度等)以及下游潮汐大小等诸多因素影响。

以闸口至盐官河段5.17 m高程下的容积作为江道冲淤面貌的特征值,对杭州段洪水位影响进行分析,主要表现在2个方面,首先是洪水流量和潮汐条件下,由于江道面貌不同引起洪水位差异明显,如1968年7月与1955年4月的洪水,闸口洪峰流量接近,分别为12 000,11 000 m3/s,但由于江道容积不同,闸口至盐官5.17 m下容积分别为2.68亿,7.98亿m3,闸口站洪水位分别为7.17,5.16 m,相差2.01m。其次是虽然闸口洪水位基本接近,但由于江道容积差异较大,闸口洪水流量也有显著差异,如1955年6月与1968年7月的洪水,闸口至盐官5.17 m下容积分别为9.31亿,2.68亿 m3,闸口洪水位比较接近,分别为7.23,7.17m,但闸口洪峰流量分别为31 000,12 000 m3/s,相差19 000 m3/s。

由此可见,洪水前期江道容积大小的估计对钱塘江河口杭州段洪水位的预报至关重要,而钱塘江河口汛期洪水对江道冲刷效果影响因素的研究,对洪水后江道冲淤面貌的估计也十分重要,同时从调度的角度看,为汛前调水冲刷适当扩大江道容积、降低洪水位、合理制定洪水调度方案、保障河口两岸平原安全度汛提供了新途径。

2 研究方法

钱塘江河口江道在汛期冲刷效果受洪峰流量、洪量、潮汐、江道起始容积大小等多种因素影响,变化十分复杂,从有限的实测资料出发,将这些因素分离出来十分困难。本文采用一维动床数学模型研究汛期洪水对江道的冲刷效果。

2.1 一维动床数学模型

由于钱塘江河口段潮波变形剧烈,河床冲淤变化多端,水流及含沙量变幅极大。因此,本模型选用了非恒定、非饱和及非耦合的挟沙水流计算模式。目前洪水冲刷明显的闸口至盐官河段,经治江缩窄后,河道已比较规则,可采用一维动床数学模型描述水沙运动,其方程为:

水流连续方程:

水流运动方程:

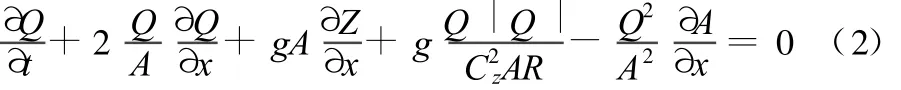
悬沙输移方程:

河床变形方程:

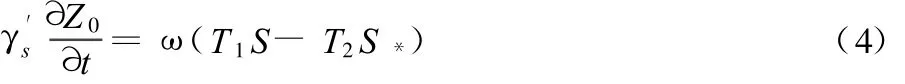
式中:x为河道里程(m);t为时间(s);Q为流量(m3/s);B为河宽(m);Z为潮位(m);A为断面过水面积(m2);Cz为谢才系数(m1/2/s);R为断面水力半径(m);S为断面平均含沙量(kg/m3);S*为断面平均挟沙能力(kg/m3);Z0为断面河底高程(m);T1、T2为无量纲泥沙冲淤系数,分别为底部含沙量与断面平均含沙量、底部挟沙力与断面平均挟沙力的比值。根据林秉南等[1]的研究成果:

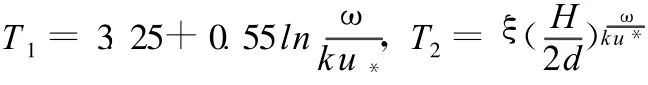
式中:ω为泥沙沉降速度(m/s)。

采用Preissmann四点偏心隐格式离散模型 (详见文献[2]),计算采用非耦合求解。

求解方程(1)～(4)需给定方程组的边界条件和初值条件,其边界条件:

上边界给定流量过程:Q(0,t)=Q0(t),当Q(0,t)＞0时,S(0,t)=S0(t);

下边界给定潮位过程:Z(l,t)=Z0(t),当Q(l,t)＞0时,S(l,t)=S1(t);

初始条件为:Z(x,0)=Z*(x),Q(x,0)=Q*(x),S(x,0)=S*(x),Z0(x,0)=Z0*(x)。

2.2 一维动床数学模型验证

本文对2010年3月上旬钱塘江河口出现的1次洪水过程进行了验证,此次洪水过程峰高量大,对河口江道冲刷明显,是近年来河口地区出现的较大洪水。钱塘江下游之江水文站实测洪峰流量达13 800 m3/s,河口地区桐庐、富阳、闻家堰、闸口等水文站最高水位分别达到10.75,8.42,7.46,6.97 m,分别超过警戒水位0.08,0.75,0.40,0.09 m。根据这次洪水过程及下游澉浦潮位过程,利用动床模型对河口地区洪水位进行了验证计算,结果见表1和图1。

表 1 2010年 “3·7” 洪水位验证成果表 m

模型对洪水前后江道冲刷也进行了验证计算,结果见表2。此次洪水过程对江道冲刷明显,闸口至盐官5.17 m下容积扩大了1.38亿m3,模型计算冲刷1.27亿m3,误差8%;其中闸口至仓前河段实测冲刷0.56亿m3,模型计算冲刷0.67亿m3;仓前至盐官河段实测冲刷0.81亿m3,计算冲刷0.59亿m3,误差均不超过30%。

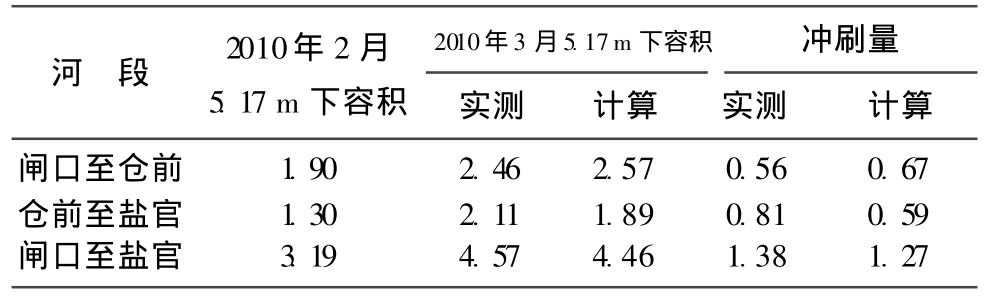
表2 2010年 “3·7”洪水冲刷量验证表 亿m3

在上述验证计算的基础上,模型对河床变形进行了长历时验证计算。2010年3—6月钱塘江上游来水较丰,钱塘江河口在 “3·7” 洪水后继续冲刷,至6月25日,闸口至盐官5.17 m下容积扩大至5.25亿m3,较汛前冲刷了2.06亿m3,模型计算冲刷了2.10亿m3,误差2%,具体河床冲刷验证见表3。由此可见,一维动床模型基本复演了2010年汛期洪水位过程及江道在洪水作用下的冲刷现象,可用于方案研究。

表3 2010年3—6月洪水冲刷量验证表 亿m3

3 影响钱塘江河口洪水冲刷效果的因素分析

洪水冲刷是一个复杂的过程,洪峰流量、历时、江道地形等因子之间呈现强烈的非线性关系,其冲刷效果与多种因素有关,如江道起始容积、洪峰流量、下游潮汐大小等,由于各个因素对冲刷效果的影响不同,逐一进行单因素分析。

3.1 江道起始容积

江道容积大小是对汛前江道面貌的反映。江道容积越小,说明汛前江道淤积越严重,进入盐官以上的潮量越小,径、潮流比值越大。图2为不同的江道容积(以闸口至盐官5.17 m下容积为指标)下,下游遭遇小潮(澉浦高潮位2.82m)情况下冲刷24 h的动床数值模拟计算冲刷量。由图2可知,在相同流量条件下,江道容积越大,冲刷量越小,如电站流量8 000 m3/s时,在容积为2.8亿m3的江道条件下,24 h冲刷0.18亿m3,在3.3亿m3的江道条件下,24 h冲刷0.15亿m3,在4.0亿m3的江道条件下,24 h仅冲刷0.11亿m3,可见随起始江道容积的扩大,冲刷效率降低;随着流量的增大,不同江道冲刷量的差值增大,如电站流量8 000 m3/s时容积为2.8亿,4.0亿m3的江道,24 h冲刷量差0.07亿m3,当流量为15 000 m3/s时,冲刷量差0.14亿m3。

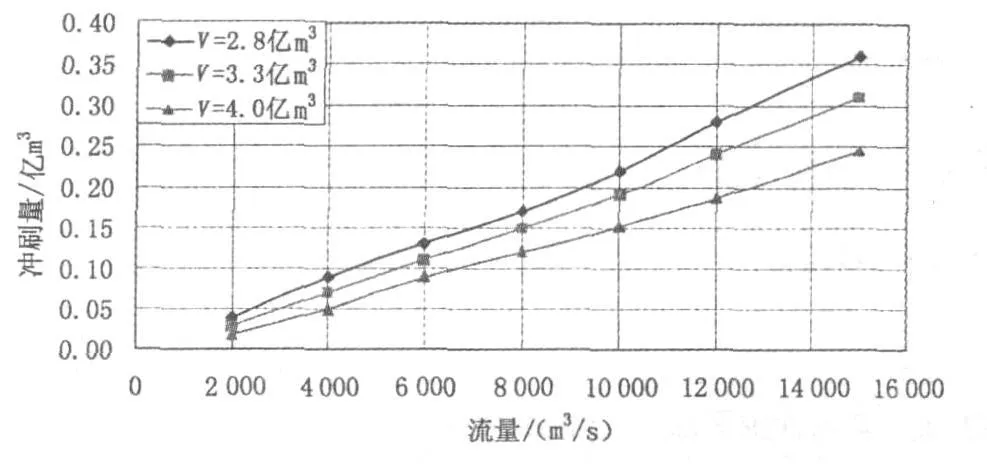
图2 不同江道条件下24 h冲刷量图

3.2 洪峰流量

水流挟沙力与流速的高次方成正比,流速越大,输沙率越大。采用水沙比反映洪水冲刷的效率,即冲刷1 m3的沙需要的水量,值越大,说明冲刷效率越低,反之则越高。图3反映了不同江道条件和流量条件下的冲刷效率。由图3可知,在同一江道地形条件下,随着流量的增大,水沙比不断减小,冲刷效率提高。

图3 不同江道、不同流量条件下冲刷效率图

3.3 潮汐大小

不同江道和潮汐条件下闸口至盐官河段24 h的冲刷量见图4。由图可知:①在流量较小的情况下,大潮期冲刷量较小潮期冲刷量大,当流量增大到一临界值后,小潮期冲刷效率比大潮期高;②随着起始江道容积的扩大,临界值也相应增大。

图4 不同潮汐、不同流量条件下冲刷量图

3.4 洪潮遭遇时刻

上游洪水的冲刷与洪、潮在闸口至盐官之间的遭遇组合有关,在上游流量一定的条件下,洪水到下游各站的历时基本是确定的,则洪潮遭遇时刻取决于富春江电站泄放时刻与澉浦潮位所处的状态。本文根据澉浦潮位所处不同状态做了2组数值试验,第1组是前期流量较小(假定为200 m3/s),分别在澉浦高潮位和低潮位时刻泄放流量为10 000 m3/s的恒定流过程;第 2组是前期流量相对较大(假定为5 000 m3/s),分别在澉浦高潮位和低潮位时刻泄放流量为10 000 m3/s的恒定流过程 (见图5)。

从泄放时刻起24 h内闸口至盐官5.17 m下容积过程见图6。由图可知,若澉浦高潮位时刻开始泄放,则在前期流量较小的情况下,4 h后由于洪水波已影响到闸口,此时闸口至盐官段均处于落潮期,闸口至盐官的容积开始增大,但冲刷速率很小,12 h后盐官开始涨潮,从冲刷过程看,12～14 h有持续2 h的容积减小过程,表明此时由于涨潮流影响发生了淤积。14 h后江道继续冲刷,且冲刷速度较前期快。

图5 洪潮遭遇径流及潮汐边界条件图

若澉浦低潮位时刻开始泄放,此时闸口至盐官河段均处于落潮阶段。在前期流量较小的情况下,4 h后洪水波影响至闸口,闸口以下开始出现一定的冲刷,此时盐官开始涨潮,泥沙随涨潮流进入该河段出现淤积,因此在随后的3 h内闸口至盐官河段主要表现为淤积;8 h以后,随着仓前以下出现落潮,闸口至盐官江道容积开始增大,至17 h盐官开始涨潮江道容积又有所减小,19 h后江道继续冲刷且冲刷速度较前期快。

从上述2种泄放时刻看,冲刷的过程有所不同,澉浦高潮位时刻泄流冲刷出现的时间较早,而澉浦低潮位时刻泄流冲刷出现的时间较迟,但在2个潮的时间内冲刷的总量基本接近。高潮时刻泄放和低潮时刻泄放造成的冲刷过程差异,主要是由于盐官段出现涨潮时刻不同造成的。

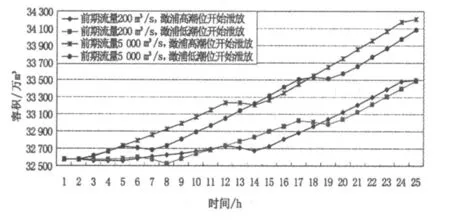
图6 不同时刻洪水泄放对闸口至盐官江道冲刷影响图

4 结 语

(1)钱塘江河口杭州段洪水位不仅受上游洪峰流量、下游潮汐强弱的影响,而且也明显受江道冲淤面貌影响。通过汛期洪水对江道冲刷效果的研究,可以定量预估洪水作用下的江道冲淤面貌,对汛期洪水位的预报具有十分重要的指导意义。

(2)洪水的冲刷效果与江道起始容积、洪峰流量、下游潮汐大小、洪潮遭遇等因素有关。数值试验分析结果表明,江道起始容积越大,洪水冲刷效率越低;洪峰流量越大,则冲刷效率越高;下游潮汐强弱的情况比较复杂,与江道容积、下泄流量均有一定的关系,但在流量较大的情况下以小潮期间的冲刷效率较高。洪潮遭遇改变了洪水冲刷的过程,但在24 h内不论如何遭遇,冲刷总量基本接近。

[1]林秉南,黄菊卿,李新春.钱塘江河口潮流输沙数学模型[J].泥沙研究,1981(2):16-17.

[2]史英标,林炳尧,徐有成.钱塘江河口洪水特性及动床数值预报模型[J],泥沙研究,2005(1):7-13.