湍流强化传热反馈控制机理

潘利生，史维秀，汪健生

(天津大学机械工程学院，天津 300072)

湍流强化传热反馈控制机理

潘利生，史维秀，汪健生

(天津大学机械工程学院，天津 300072)

对流换热与湍流结构密切相关，运用大涡模拟方法，在湍流流场中进行强化传热反馈控制，分别采用3种反馈控制速度，研究反馈控制对传热的影响机理和效果，并建立目标函数，研究平均强化传热效果．结果表明：在湍流流场中输入适当反馈控制，强化传热效果明显；当α为5.0、10.0和15.0时，努塞尔数最大增幅分别为8.78%、11.17%和14.08%，平均增幅分别为4.80%、6.88%和9.09%；当α为15.0时，y+＝5处流场温度比未输入反馈控制的流场高10,℃左右．

反馈控制；强化传热；大涡模拟；湍流拟序结构

反馈控制能够以很小的能量输入而达到对湍流的完全控制，因此备受关注．文献[1-3]研究表明，在近壁面区域进行反馈控制，最多可以使壁面摩擦阻力降低25%．在中等雷诺数及以下，采用直接数值模拟和大涡模拟进行反馈控制的研究已取得了显著成果[4]．

Choi等[1]于1994年应用一种所谓主动取消法(active cancellation)，依据近壁面区域的法向速度(y+＝10)，在壁面进行吹/吸操作而使得壁面摩擦阻力降低了25%．Lee等[2]于1998年提出了一种新的以壁面变量为参照的亚优法则，这些变量为展向壁面剪切应力和壁面压力波动．同时Lee等[5]于1997年引入了神经网络并在直接数值模拟槽道时获得了20%的阻力降低．Endo等[6]于2000年对槽道进行了直接数值模拟，所采用的控制方法是通过布置一系列离散的壁面传感器和可以变形的控制器，发现这种真实的控制单元可以推动阻力在实际中的降低．随着直接数值模拟应用到高雷诺数的情况，Iwamoto等[7]于2002年认为无论是主动取消法还是亚优化控制模式在高雷诺数的槽道流动中所起的作用不大．

MEMS(micro-electro-mechanical systems)的一个重要应用舞台就是流动控制，MEMS传感器和控制器为湍流拟序结构的控制创造了机会[8]．虽然边界层附近的湍流结构非常微小，但是随着MEMS的发展，构建亚毫米级的流动传感器是完全可能的．Lundell[9]对传感器和执行器的结构布置进行研究，采用交叉结构来优化控制．

众多学者应用反馈控制，在湍流减阻方面取得了不少成果，对线性反馈控制[10]的研究也逐渐增多，尽管湍流强化传热的技术[11]仍在不断进步，但较少关注反馈控制对传热的影响，也较少将反馈控制应用于强化传热方面．笔者基于强化传热的目的，应用大涡模拟方法，研究反馈控制湍流强化传热的机理和效果．

1 数值计算模型及控制方程

湍流流场为长方形槽道，见图1．槽道中流体沿x正方向流动．控制方程为不可压缩Navier-Stokes方程和连续性方程．流向(x向)和展向(z向)为周期性边界条件，顶面和地面为无滑移壁面．底面热边界条件为定温．

流向、展向和法向的计算区域分别为2πδ、πδ和2δ．其中δ为槽道的半高度．数值模拟计算在定流量情况下进行，雷诺数为160．本文以后提到的()+是基于壁面剪切速度uτ和运动黏度v的无量纲数．

流向、展向和法向3个方向的网格数都为72．法向采用非均匀网格，第1层网格在距离壁面y+＝0.46的位置．数值计算时间步长选择为Δt+＝0.25．反馈控制输入前的流场为由LES获得的充分发展湍流流场．

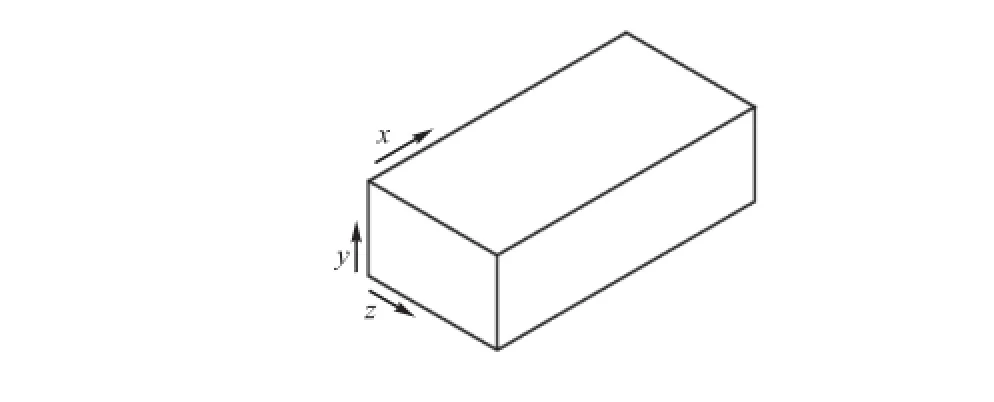
图1 计算模型示意Fig.1 Schematic diagram of simulation model

大涡模拟将湍流划分成大尺度涡和小尺度涡．大尺度涡直接进行求解，而小尺度涡采用模型来求解．在数值计算中，采用Deardorff box滤波模型来划分大尺度涡和小尺度涡的湍流参数．对于不可压缩流体，大涡模拟中的质量守恒方程、动量守恒方程和能量守恒方程如下．

质量守恒方程

动量守恒方程

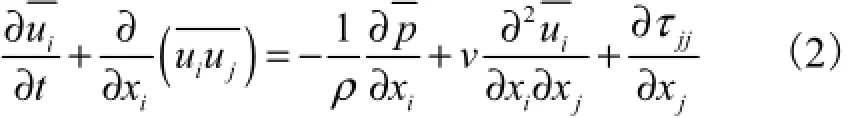
能量守恒方程

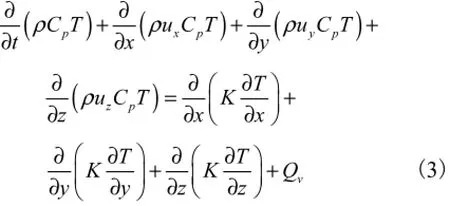
2 计算结果与分析

2.1 湍流拟序结构

运用大涡模拟对计算区域进行计算，获得充分发展湍流流场．充分发展的湍流，在近壁面区域，猝发过程伴随着低速流体的堆积，逐渐形成低速流体向外喷射和高速流体向内扫掠，低速流体和高速流体的间歇出现形成了条纹结构．图2为y+＝10的法向截面的条纹结构．

图2 y+＝10处的条纹结构Fig.2 Stripe structure at y+＝10

近壁面区准流向涡被证明对湍流速度边界层和热边界层起主要作用，对外区流场影响很大．图3所示为某流向截面的流向涡结构，从图中可以看出，在近壁面区域存在着大量流向涡，这些涡结构数量上多于核心区，对近壁面区域的阻力和换热影响很大．为了达到强化传热的目的，必须对近壁面区域的流向涡加以研究和控制．

图3 某流向截面的流向涡结构Fig.3 Streamwise vorticities at a streamwise cross section

2.2 反馈控制模式

Choi等[1]于1994年提出法向速度控制方法(V-control)，通过在y+＝10～15处监测流场，在底面进行吹/吸控制，能够达到减弱壁面涡结构的作用．

经过充分发展湍流数值计算，在y+＝10处可以很好地监测到近壁面区域的第1层准流向涡结构．故在y+＝10处设置监测面，监测此面内的法向速度和展向速度，然后将监测结果返回到控制程序，进行判断，若监测结果显示近壁面区域存在准流向涡结构，则在壁面采取V-control方法进行控制操作，见图4．在V-control中，控制速度表达式为

分别取α为5.0、10.0和15.0进行数值计算．然后对比不同控制速度下的底面传热情况．

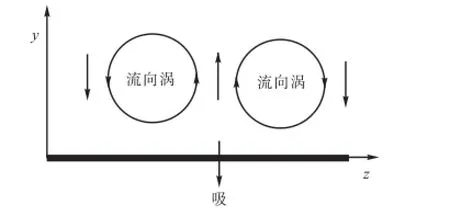
图4 反馈控制示意Fig.4 Sketch map of feedback control method

2.3 强化传热机理

在湍流流场中，近壁面区域基本由相对强的准流向涡所占据，这些涡与近壁面区域流体的喷出和扫掠过程紧密相关，并且是近壁区雷诺应力产生的根源，缓冲层的流向涡在低速条纹形成中起明显的作用．准流向涡常常以非对称反转涡对出现，有时也呈单个出现．

在近壁面区域，由于准流向涡的作用，不断地有流体从壁面区域向外喷射，有流体从外区下扫．流体向外喷射减小近壁面区域的速度梯度和温度梯度，流体下扫有利于增大近壁面区域速度梯度和温度梯度，减薄速度边界层和温度边界层，有利于传热的加强．故在近壁面区域设置监测面监测流场，当监测到的信息显示近壁面区域存在准流向涡并将形成流体向外喷射时，即时采取控制，抑制流体向上喷出，尽量形成下扫，减薄速度边界层和温度边界层，以达到强化传热的目的．

2.4 反馈控制对传热的效果分析图5为同一时刻，y+＝10处温度场云图．从图中可以看出，在反馈控制输入区域之前，温度场基本相同，在反馈控制区域输入控制的流场，换热得到加强，温度场温度显著提高，流场最高温度较未输入反馈控制的流场高10,℃左右．

图5 y+＝10处的温度分布云图Fig.5 Contour of temperature at y+＝10

图6 为壁面努塞尔数随无量纲时间的变化情况．从图6中可以看出，通过在充分发展湍流近壁面区域输入反馈控制，壁面努塞尔数显著提高：

在t+＝0时输入反馈控制后，努塞尔数突然增大，当α＝5.0时，增幅可达25.87%，当α＝10.0时，增幅可达32.27%，当α＝15.0时，增幅可达38.98%．在近壁面流场中输入法向反馈控制，即使是很小的能量输入，也能大幅度减薄温度边界层，从而在输入反馈控制之初，强化传热效果异常明显．

t+增加到100以后，强化传热效果趋于平缓，努塞尔数比随时间呈现波浪型变化，当α＝5.0时，最大增幅可达8.78%，当α＝10.0时，最大增幅可达11.17%，当α＝15.0时，最大增幅可达14.08%．

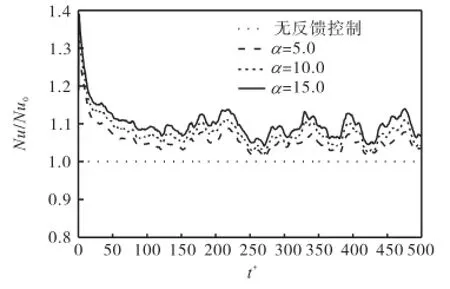
图6 壁面努塞尔数变化Fig.6 Variation of Nusselt number ratio at bottom

3种输入反馈控制的情况下，努塞尔数随时间的变化趋势相似．由于在近壁面输入反馈控制的能量非常小，对流场的整体流动状况影响很小，只是减薄了近壁面区域边界层厚度，强化了传热，故3种反馈控制下，努塞尔数的变化趋势相同．

湍流流场和传热效果随时间不断变化，经过反馈控制，强化传热的效果随时间不尽相同．故最大强化传热数值并不能完全反映综合强化传热效果，有必要研究在计算时间范围内，强化传热的平均值．为研究当反馈控制作用达到平稳后，反馈控制对强化传热的平均效果，建立目标函数为

式中：h为对流换热系数；λ为流体导热系数；1t+为初始计算时间；2t+为终止计算时间；Nu为输入反馈控制的努塞尔数；0Nu为未输入反馈控制的努塞尔数．

鉴于在反馈控制之初，反馈控制效果不稳定，努塞尔数变化剧烈，为研究反馈控制的平均传热效果，将t+＝100之前视为反馈控制非平稳区，重点研究t+在100～500范围内Nu/Nu0的平均值．应用式(6)对3种反馈控制作用下数据进行处理．计算结果表明，t+在100～500范围内，当α＝5.0时，努塞尔数平均增幅为4.80%，当α＝10.0时，努塞尔数平均增幅为6.88%，当α＝15.0时，努塞尔数平均增幅为9.09%．

表1给出了3种反馈控制情况下，努塞尔数的最大增幅和平均增幅．

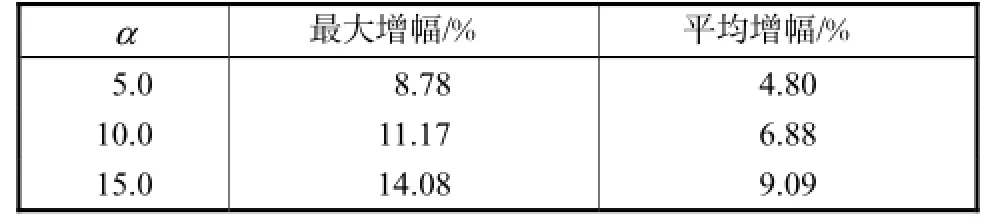
表1 不同反馈控制速度时的强化传热效果对比Tab.1 Comparison of heat transfer enhancement effects with different control velocities

3 结 论

(1)在近壁面区域输入适当反馈控制，可以显著增强换热．

(2)当α＝5.0时，最大增幅可达8.78%；当α＝ 10.0时，最大增幅可达11.17%；当α＝15.0时，最大增幅可达14.08%．

(3)引入目标函数，研究平均强化传热效果，t+在100～500范围内，当α＝5.0时，努塞尔数平均增幅为4.80%；当α＝10.0时，努塞尔数平均增幅为6.88%；当α＝15.0时，努塞尔数平均增幅为9.09%．

［1］ Choi H，Moin P，Kim J. Active turbulence control for drag reduction in wall bounded flows[J]. Fluid Mech，1994，262：75-110.

［2］ Lee C，Kim J，Choi H. Suboptimal control of turbulent channel flow for drag reduction[J]. Fluid Mech，1998，358：245-258.

［3］ Min T，Kim J. Effects of hydrophobic surface on skinfriction drag[J]. Physics of Fluids，2004，16(7)：55-58.

［4］ Kim J. Control of turbulent boundary layers[J]. Physics of Fluids，2003，15(5)：1093-1105.

［5］ Lee C，Kim J，Babcock R. Application of neural networks to turbulence control for drag reduction[J]. Physics of Fluids，1997，9(6)：1740-1747.

［6］ Endo t，Kasagi N，Suzuki Y. Feedback control of wall turbulence with wall deformation[J]. Heat Fluid Flow，2000，21(5)：568-575.

［7］ Iwamoto K，Suzuki Y，Kasagi N. Reynolds number

effect on wall turbulence：Toward effective feedback

control[J]. Heat Fluid Flow，2002，23(5)：678-689.［8］ Lofdahl L˙˙，Gad-el-Hak M. MEMS applications in turbulence and flow control[J]. Progress in Aerospace Sciences，1999，35(2)：101-203.

［9］ Lundell F. Reactive control of transition induced by freestream turbulence：An experimental demonstration[J]. Fluid Mech，2007，585：41-71.

［10］ Monokrousos A，Brandt L，Schlatter P，et al. DNS and LES of estimation and control of transition in boundary layers subject[J]. Heat and Fluid Flow，2008，29(3)：841-855.

［11］ Yang Yue-Tzu，Hwang Ming-Lu. Numerical simulation of turbulent fluid flow and heat transfer characteristics in heat exchangers fitted with porous media[J]. Heat and Mass Transfer，2009，52(13/14)：2956-2965.

Feedback Control Mechanism for Turbulent Heat Transfer Enhancement

PAN Li-sheng，SHI Wei-xiu，WANG Jian-sheng
(School of Mechanical Engineering，Tianjin University，Tianjin 300072，China)

Convective heat transfer is closely related to turbulence structure. Using large eddy simulation(LES)，feedback control was executed in turbulent flow field with three kinds of control velocities，mechanism and effect of feedback control upon heat transfer were studied，and an objective function was established to study the average effect on heat transfer enhancement. The results show that，inputting feedback control in turbulent flow field，the heat transfer is enhanced remarkably. When α is 5.0，10.0 and 15.0，the largest enhancements of Nusselt number are 8.78%，11.17% and 14.08%，respectively，and the averages of which are 4.80%，6.88% and 9.09% respectively. When α is 15.0，the highest temperature is about 10 ℃ higher than that without control at y+＝5.

feedback-control；heat transfer enhancement；large eddy simulation；turbulent coherent structure

TK124

A

0493-2137(2011)07-0655-04

2010-04-02；

2010-06-01.

国家自然科学基金资助项目(50976079)；国家高技术研究发展计划(863计划)资助项目(2009AA05Z431).

潘利生（1982— ），男，博士研究生.

潘利生，Lisheng_P@163.com.