基于产品性能-成本-交货期的多目标优化配置研究
2011-07-07华尔天曹魏魏刘科红
华尔天,陈 颖,曹魏魏,刘科红
(浙江工商大学 计算机与信息工程学院,杭州 310018)
0 引言
产品配置设计是一种快速设计方法,通过合理组织已有的设计成果,根据用户需求选择零部件迅速组成新产品,缩短产品设计时间和上市周期,提高企业竞争力[1,2]。产品配置的目标就是找出满足配置约束条件和用户需求的可行方案[3],许多学者已对产品配置优化设计进行了深入研究[4~6]。文献[7]通过分析机械产品生命周期的生产成本和经济损失,构建多目标产品成本价值与可靠度的关系模型,得到机械产品生命周期的多目标优化设计方案;文献[8]以阻力墙结构参数为变量,建立模具磨损和成形载荷的Kriging模型,并采用线性加权法将模型转化为单目标函数,得到优化结果;文献[9]考虑制品质量均衡性以及生产的成本和效率,建立注塑模流道多目标优化设计数学模型,最终利用细粒度模型获取能使综合指标最优的设计方案;文献[10]采用最优拉丁试验设计及最小二乘方法构建多目标优化系统的各个目标及约束性能参数的模型,利用NSGA-Ⅱ对多目标优化模型进行优化,得到满足约束的最优方案。但是上述文献所考虑的优化目标多为单一静态的,而在实际中产品配置方案随客户的需求侧重点不同而动态变化。如何针对客户对需求的侧重点不同而得到最优的产品配置方案,是当前学界和业界关注的重要课题。针对上述问题,本文建立了基于产品优化配置参数的多目标函数优化模型,并对其进行动态求解,得到满足用户需求的优化方案。
1 产品优化配置参数
产品优化配置参数主要包括产品性能、产品成本以及产品交货期。用户追求的就是产品的最佳性能、最小成本以及最短的交货期。对于不同的用户,对这三方面的参数要求权重会各不相同,侧重点也会因人而异,使得产品性能、成本及交货期三个参数的动态变化尤为重要。在产品性能方面通过对用户的大量问卷调查,调查用户对产品性能满意度,由产品综合性能最优原则选取性能最优的设计方案予以实施;产品成本包括了产品各个部件的固定成本以及除原材料外的固定成本,如设备损耗费、燃油费、工人工资等费用;交货期要保证及时交货。
本文以产品性能-成本-交货期为出发点,结合模糊数学理论,构建以产品性能-成本-交货期为目标函数的多目标配置优化函数,提出了一种基于多目标差异演化算法的产品配置优化方法对其进行并行优化,得到一系列配置方案的Pareto集以满足客户的不同要求。
2 产品优化配置模型
2.1 产品性能的优化配置模型
令产品的性能矢量为P=(P1, P2, , PD)T,Pd为产品的第d个性能,d=1, 2, , D,D为产品性能项总数,对应的权重矢量为WP=(w1, w2, , wd)T。
构建产品性能的关联度矩阵

其中:ij为满足第j项性能需求(j=1, 2, , m)的第i个零部件(i=1, 2, , k)的相关度,其量化值可用模糊数学评价理论中的极强相关、强相关、中相关、弱相关或无相关表示,令相对值衡量度分别为:9, 7, 4, 1, 0。
则产品性能的优化模型:

其中:Pz为产品性能的评价指标,其值越高,则产品性能越好;ij为二元决策变量,表示第i个构件在产品配置中是否被选择,选中时取1,未选中为0;wd为产品性能集的权重量。
2.2 产品成本的优化配置模型
构建产品成本矩阵:

其中:cij为满足第j项性能需求的第i个构件的成本。
配置的产品总成本要能够保证小于客户所能承受的最高价格,则产品成本优化模型为:
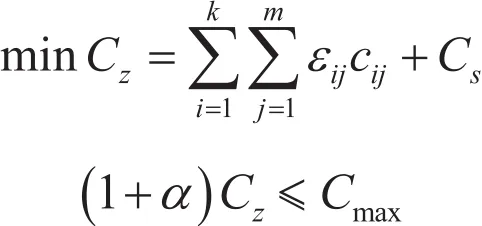
其中:Cz为配置产品的总成本;Cs为产品配置的一切固定成本,如设备耗损、维修费等;为企业利润;Cmax为客户能承受的最高价格。
2.3 产品交货期的优化配置模型
构建产品的交货期矩阵:

其中:tij为选中满足第j个性能需求的第i个构件对产品交货期的延迟。
产品配置不仅要满足客户需求,还要保证交货及时,产品交货期优化函数可以表示为:

其中:Tz为配置产品的交货期,Tmax为客户允许的配置产品最大交货期。
2.4 约束条件的建立
1)配置约束条件
产品配置时,部件之间存在着两两互斥或两两相容的关系。引入变量Qij表示零件qi与零件qj之间的相容程度,则约束关系表示为:

2)成本约束条件: (1+) Cz≤Cmax
3)交货期约束条件: Tz≤Tmax
2.5 产品多目标优化配置模型
通过对产品配置优化模型的建模分析可知,上述产品配置优化模型的求解属于典型的有约束多目标优化问题。结合约束条件,将多目标配置优化模型转化为如下数学模型:

其中:Pz(X)是效益型目标函数,其值越大越好;Cz(X), Tz(X)是成本型函数,其值越小越好;ga(X)为优化模型的不等式约束;hb(X)为优化模型的等式约束,a和b分别表示不等式约束和等式约束的个数。
根据上述模型,本文的数学模型描述如下:

考虑到传统的目标函数线性加权法不能保证Pareto的优化解,本文采用基于多目标演化算法对上述配置优化模型进行求解。
3 产品优化配置模型算法
3.1 差异演化算法
差异演化算法(DE)是近几年新兴的一种新的进化算法,是求解Pareto优化解的有效手段,将其引入多目标优化,可在一次优化过程中就产生一组非劣解,使得优化过程直接面向Pareto优化解进行,避免了集成算法的缺点,可直接用于多目标优化问题[11]。差异演化算法中的主要程序包括了生成初始种群、变异操作、交叉操作以及选择操作。
令xi(g)为第g代的第i个个体,则

3.2 差异演化算法的改进
多目标差异演化算法(MODE)则引入群体中心点,并在差异演化算法的基础上做一定的改进。
定义第t代群体中心点:

其中:Cp为群体中心点,随着代数的变化而变化[12]。
3.2.1 变异操作
MODE变异操作定义为:
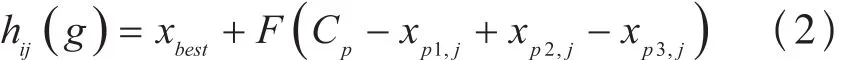
其中:xbest是从当前种群中随机取出的,xp1、xp2、xp3是从初始化种群中随机取出的三个个体。
3.2.2 线性递增交叉操作
交叉操作定义为:

其中:rand (1, n)为[1, n]之间的随机整数。Pc为交叉概率,一般都在[0,1]之间选择,比较好的选择是0.3左右[13]。通常在交叉操作中Pc的取值在[0.9,1]之间时容易收敛。本文采用线性递增交叉策略,调整算法的交叉率,加快算法的收敛速度,也尽量避免发生“早熟”现象。
线性递增交叉率定义为:

其中:PCmin为交叉率的最小值,取值0.1;PCmax为交叉率的最大值,取值0.9;Tmax为最大进化代数,iter当前进化代数。
3.2.3 选择操作
评价函数在父代个体向量vi(g+1)和子代个体向量xi(g)之间进行比较。

综上所述,多目标差异演化算法的实施过程如下:
1)设置算法相关控制参数及变量的范围:N-种群规模、 F-缩放因子、Pc-交叉概率、Tmax-最大迭代代数,终止条件;
2)初始化种群P(0),t=O;
3)计算种群P(t)中每个个体的适应度,构建外部种群;
4)由式(2)在可行域内进行变异操作;
5)由式(4)表示的线性递增交叉率,根据公式(3)在可行域内对种群进行交叉操作;
6)按根据公式(5)的方法对父代和子代进行选择操作;
7)更新外部种群,将前面计算得到的可行域内的个体与外部种群进行合并,合并后对其按快速排序法进行选择非支配集;
8)判断是否达到最大进化代数(或达到所要求的收敛精度),若是,则输出优化解。否则,进化代数加1(t=t+l),返回4),继续运行。
4 应用实例
以某厂生产的儿童手推车为例,运用MODE对其进行配置优化,最终得到最优设计结果。表1为儿童车推车的参数设计表。

表1 儿童手推车主要设计参数表
对产品的设计参数构建相关度矩阵,根据大量的客户问卷调查表,利用层次分析法(AHP)得到儿童手推车的性能权重分配关系为 ={0.1392 0.1098 0.098 0.1059 0.0882 0.0775 0.0814 0.0794 0.0735 0.0706 0.0765}
根据表1中儿童手推车的主要设计参数的不同,对其进行组合,共得到81个版本的儿童手推车,根据不同零部件的组成,对制造成本和交货期进行分析,可以得到不同版本儿童手推车的制造成本和交货期,如表2所示。
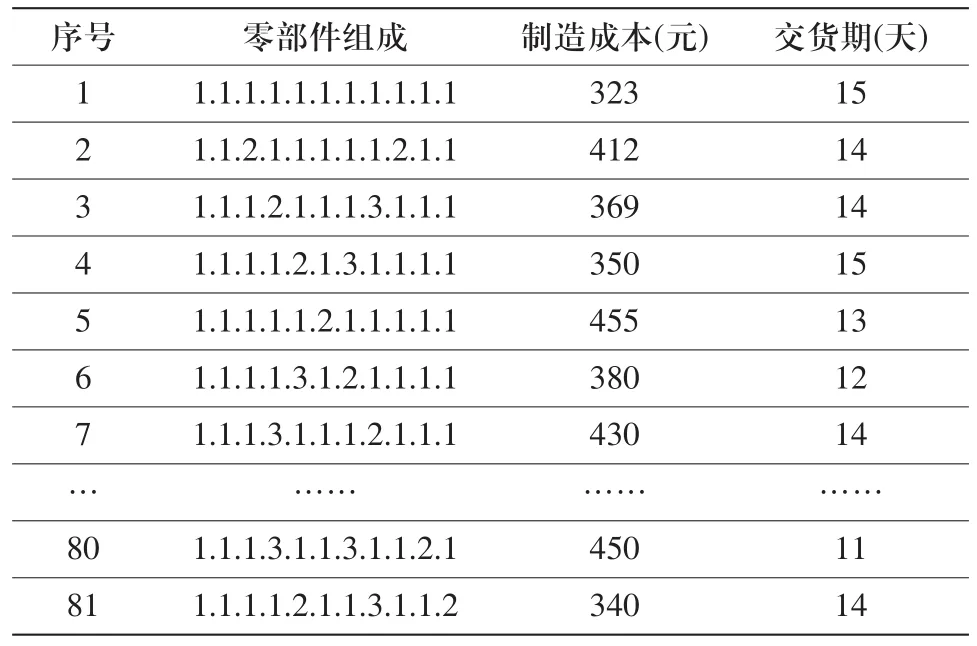
表2 不同组成儿童手推车的成本和交货期
运用MODE的步骤,以二元决策变量ij为设计变量,以儿童手推车的性能Pz最大,制造成本Cz、交货期Tz最小为目标函数,在满足约束条件的前提下进行产品优化配置。基于MODE的特点,令其种群数目为100,最大进化代数为300,缩放因子F选取在(0.1, 0.9)之间的随机数,交叉概率Pc选取在(0.1, 0.9)之间,并按照进化代数线性递增。应用Matlab进行产品优化配置仿真的过程与结果,得到目标函数的动态变化曲线。如图2所示。
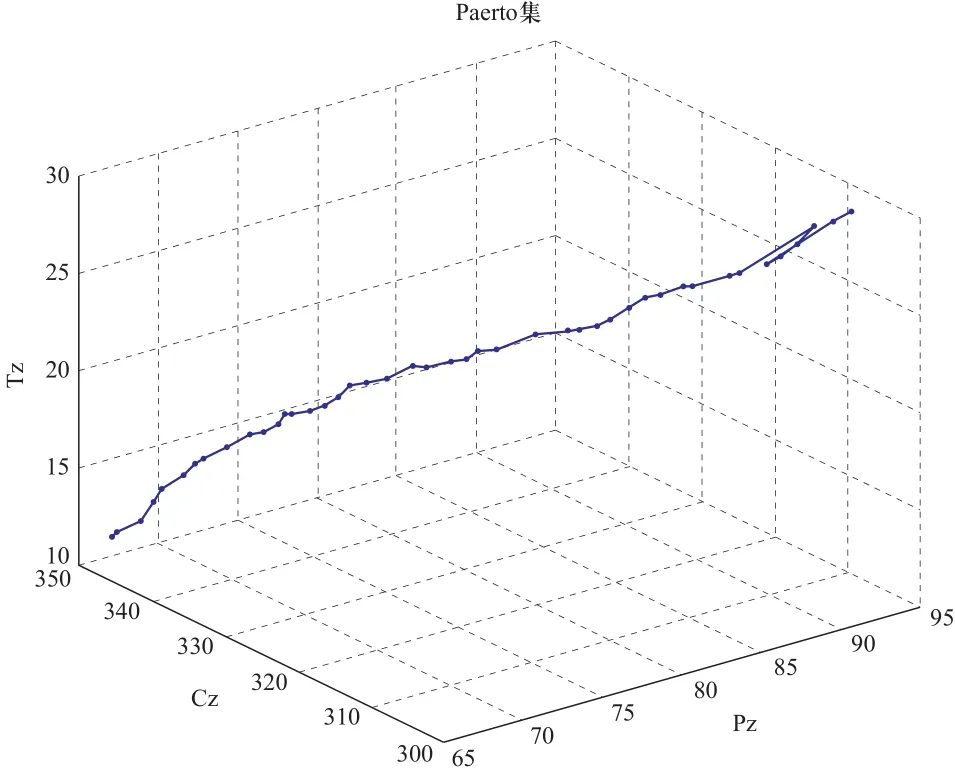
图2 配置方案的Pareto集
客户可以根据自己对每个目标的重要程度的不同来选择,从相应的Pareto集中找到这一点的设计变量值,得到客户所需的产品配置方案。表3为从中选取的3种优化方案。

表3 根据不同客户需求的两种配置方案
企业将这三种配置优化方案提供给客户进行选择,从产品性能-成本-交货期的综合考虑确定最满意的配置方案。在考虑各种因素后,客户最终选择方案2,既能达到产品的性能要求,又使得较少的产品成本和较短的交货期。
5 结论
传统的产品配置方案大多都基于知识、约束或经验来求解,在产品的具体配置过程中没有过多考虑客户的需求。本文提出以产品性能、成本及交货期为目标函数的多目标优化配置数学模型,通过MODE对模型进行求解,得到了一组基于Pareto集的多目标优化配置方案,实现产品设计的动态模式,满足不同客户从不同角度对产品的不同要求。通过对儿童手推车实例的分析,证明了该方法的可行性和有效性,为大规模定制个性化产品提供了有效的方法。
[1] Freek Erens,Karel Verhulst. Architectures for product families. Computers in Industry, 1997, 33: 165-178.
[2] Chao Ping Yi, Chen Tsung Te. Analysis of Assembly through Product Configuration. Computers in Industry,2001, 44: 189-203.
[3] 李斌, 陈立平, 钟毅芳. 基于多目标遗传算法的产品优化配置研究[J]. 中国机械工程. 2004, 15(20): 1819-1875.
[4] 周宏明, 李峰平, 薛伟, 等.基于构件的产品配置模型和实现方法研究[J]. 中国机械工程. 2006, 10(24): 2577-2581.
[5] CHA KRAVARTY A C, BALA KRISHNAN N. Achieving product variety through optimal choice of module variations [J]. IEEE Transactions, 2001, 33 (7): 5872-5981.
[6] 徐燕申, 陈永亮. 机械产品快速响应设计/制造的关键技术及其应用[J]. 航空制造技术. 2003 (4): 672-701.
[7] 钱松荣. 机械产品生命周期的多目标优化设计方法[J].机械设计与制造. 2010, 9: 149-151.
[8] 周杰, 张渝, 安治国, 等. 基于遗传算法的锻模阻力墙结构多目标优化[J]. 机械工程学报. 2010. 7. 46(14): 86-90.[9] 程锦, 谭建荣, 魏巍. 基于变粒度的注塑模流道多目标优化设计[J]. 机械工程学报. 2010. 3. 46(6): 170-175.
[10] 胡朝辉, 成艾国, 等. 多材料一多零件规格组合结构多目标优化的应用[J]. 机械工程学报. 2010. 11. 46(22):111-116.
[11] 袁俊刚, 孙治国, 曲广吉. 差异演化算法应用问题研究[J]. 计算机工程与应用. 2007, 43(7): 75-77.
[12] 李明磊, 贾育秦, 张学良, 等. 基于多目标差异演化算法的并联机构结构优化[J]. 中国机械工程. 2010, 21(16):1915-1920.
[13] 温淑华, 张学良. 差异演化算法及其在机械优化设计中的应用[J]. 农业机械学报, 2008. 39(8): 135-139.
