快速计算多个卷积的新方法及其应用

范安东 李小伟 王 娜 肖思和

（成都理工大学 数学地质四川省重点实验室，成都610059）

通过将2个N点实序列x（n）和y（n）组合成一个N 点复序列z（n）＝x（n）＋jy（n）的方法就可以同时计算出它们各自对应的离散傅里叶变换（discrete Fourier transform，DFT），并能够节约计算 量 和 存 储 空 间［1，2］。1999 年 和 2002 年，Moshe、Hertz［3］和 Gunther［4］又先后提出了同时计算实序列的DFT和逆离散傅里叶变换（inverse discrete Fourier transform，IDFT）的直接公式。Moshe和Hertz的算法还曾被推广到二维实序列和有 限 域 Fq2 上 的 Mersenne变 换 上 去［5，6］；而Gunther提出的算法也被推广到二维的情况［7］，并应用于数字水印嵌入取得了较好的效果［8］。

由文献［4］可知，对于给定的X（k）和y（n），通过计算复序列z（n）的DFT（记为Z（k）），x（n）（X（k）对应的IDFT）和Y（k）（y（n）对应的 DFT）可由表1中的任一行给出的公式直接求出。

这里X＊（n）表示X（n）的共轭，（－n）N表示－n模N的最小非负剩余。在文献［8］中，范安东等指出了表1中第4组公式的错误和文献［4］中同时计算2个N点实序列的DFT公式中的错误，并进行了改正，给出了相关正确公式的严格证明（文献［4］中只给出了表1中的结果，未提供任何证明）。

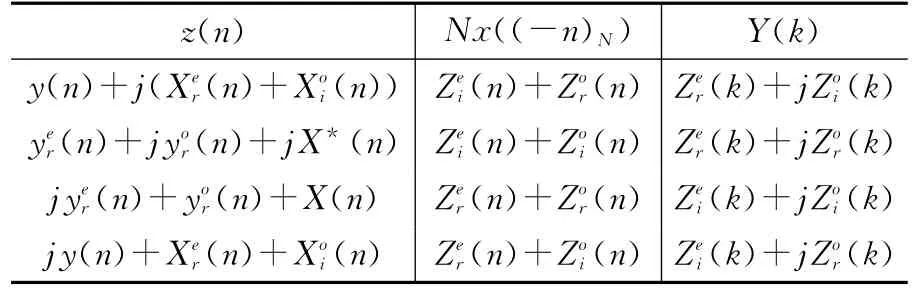
表1 同时计算N点实序列的DFT和N点实序列的DFT的IDFT的新公式Table 1 New formulas for simultaneously calculating DFT and IDFT of two real N－point sequences

1 DFT的一些性质

本节介绍DFT的一些相关性质，特别是实序列的 DFT 的一些性质［4，8－10］。

性质1设x（n）是一个N 点实序列，则X（k）是Hermitian对称的，即

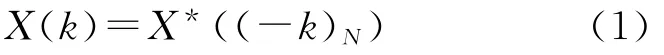
这里k＝0，1，…，N－1。

注1：如无特殊说明，本文中变量n和k的取值范围均表示为：n，k＝0，1，…，N－1。

性质2设x（n）是一个N 点实序列，x（n）的DFT为X（k），X（n）的 DFT为则

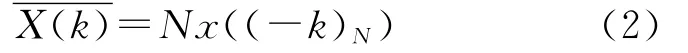
性质3设a（n）是一个N点复序列，则a（n）可以分解为下面4个N点序列之和

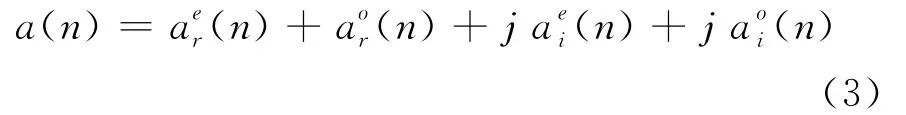
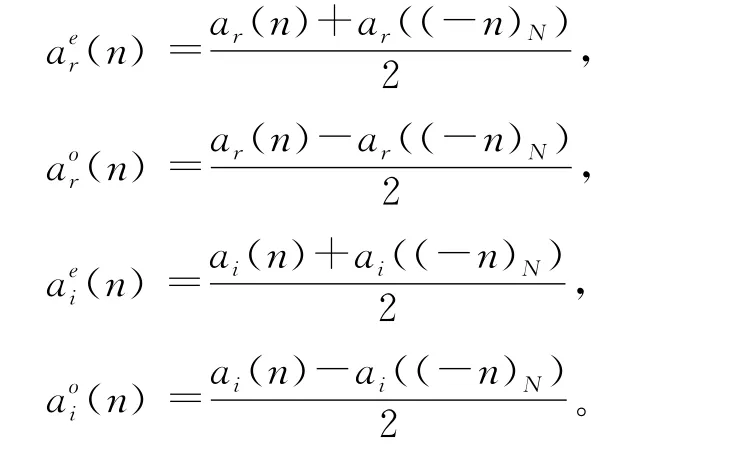
性质4

1）x（n）是实偶序列⇔X（k）是实偶序列。

2）x（n）是实奇序列⇔X（k）是纯虚奇序列。

性质5设x（n）是一个N 点实序列，把X（k）分解为形如（3）式，则

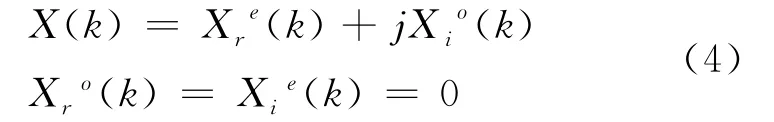
引理［8］（同时计算2个实序列的DFT的一个新公式）

设x（n）和y（n）是2个N 点实序列，且令z（n）＝x（n）＋jy（n），则

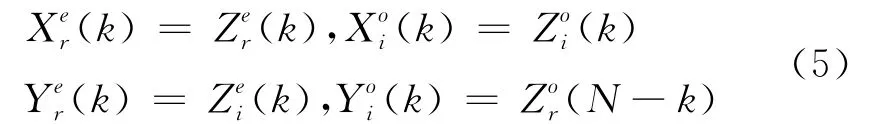
其中

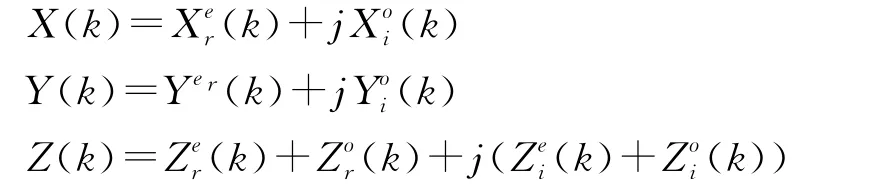
这里X（k）、Y（k）和Z（k）分别是x（n）、y（n）和z（n）的DFT。

2 同时计算y（n）的DFT和X（k）的IDFT的新公式及其在卷积计算中的应用

2.1 新公式

本节假定x（n）和y（n）是2个N 点实序列，X（k）是x（n）的DFT，y（n）和X（k）是给定的，要求通过计算一个N点复序列z（n）的DFT（设为Z（k））同时求出x（n）和Y（k）的值。由性质3和5可知，y（n）可由（n）和（n）决定，X（k）可由（k）和（k）决定。

利用上面讨论的DFT的一些性质和引理不难得到下面的结果。

定理1（同时计算实序列的DFT和IDFT的新公式）设

如果

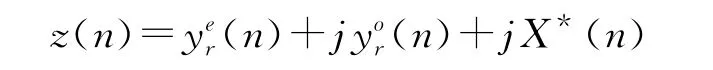
则

注2：本定理改正了文献［4］表1中第2行所给出的公式，更正后公式的正确性可用上节给出的引理和DFT的一些性质进行证明，详细证明请参阅文献［12］。

2.2 传统的卷积计算方法

循环卷积是数字信号处理中经常用到的一个重要运算。由于循环卷积和离散傅里叶变换在数学定义形式上存在一定的内在联系，通过分析易知计算2个信号的卷积可通过计算2个DFT和1个IDFT来完成，而DFT和IDFT的计算又存在快速算法（FFT和IFFT），故在实际应用中一般都是通过DFT来计算信号的卷积。

定理2［2，11］记长度为 N 的2个序列x（n）和h（n）（其中n＝0，1，…，N－1），它们的循环卷积为

这里（n－k）N表示n－k模N 的最小非负剩余。

记x（n）的 DFT 为 X（k），h（n）的 DFT 为H（k），Y（k）的IDFT为y（n），则有

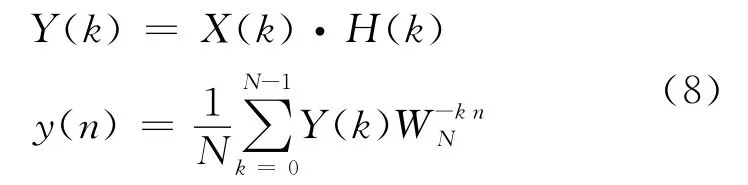
上述定理称为循环卷积定理。该定理说明只要先分别计算出x（n）和h（n）的DFT，然后将它们相乘即可得到x（n）和h（n）的卷积的DFT，最后再做一次IDFT即可得到x（n）和h（n）的卷积。

利用定理2，可以得到传统的计算卷积的过程：

1）计算x（n）和h（n）的DFT

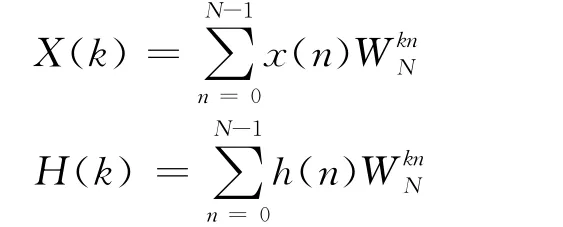
2）计算X（k）和 H（k）乘积

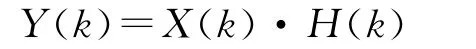
3）计算Y（k）的IDFT

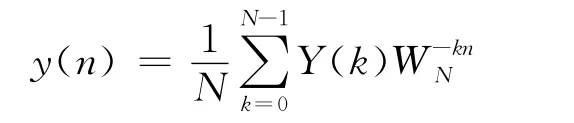
从上面的计算过程可以看出求2个长为N的实序列的卷积需要计算2个一维N点DFT和1个一维N点IDFT。据此推算，当计算m个长为N的实序列所构成的信号簇通过一个滤波器的输出时，使用传统的方法计算此m个卷积需要计算m＋1个一维N点DFT和m个一维N点IDFT。

2.3 新公式在计算多个卷积中的应用

从上一小节中可以看到，当计算由m个长为N的序列所构成的信号簇通过一个滤波器的输出时，使用传统的计算方法其计算量还是比较大的。本小节将引入同时计算实序列的DFT与IDFT的新公式，得到新的计算一维卷积的方法。

假设一簇信号｛xi（n），（i＝0，1，…，m－1）｝通过一个滤波器h（n），滤波器的输出分别为｛yi（n），（i＝0，1，…，m－1）｝。根据引理和定理1可以得到新的计算m个信号组成的信号簇通过一个滤波器的一维循环卷积算法。新算法的流程如图1所示。

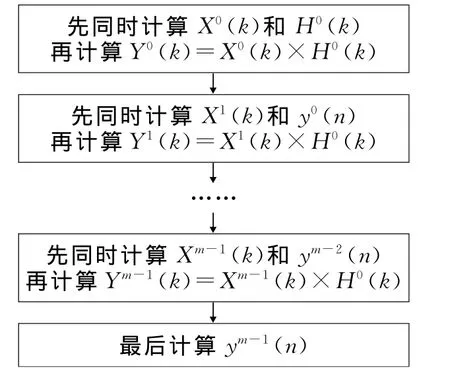
图1 m个一维卷积运算的新算法流程图The flow chart of a new algorithm for computing the convolution of a m－serial

首先设信号簇｛xi（n）｝的 DFT为｛Xi（k）｝，滤波器h（n）的 DFT 为 H（k），滤波器的输出｛yi（n）｝的 DFT为｛Yi（k）｝，则新的计算卷积的过程如下：

第1步设z（n）＝x0（n）＋jh（n），利用引理，可同时得到x0（n）和h（n）的DFT：

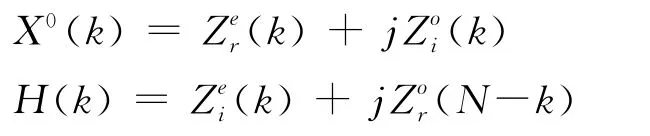
再计算

注3：H（k）在后面的计算过程中还要用到，由于滤波器的脉冲响应总是相对固定的，因此可以在进行正式的滤波处理之前将H（k）先计算出来备用。

第2步不妨记x（n）＝x1（n），Y（k）＝Y0（k），y（n）＝y0（n），X（k）＝X1（k），设

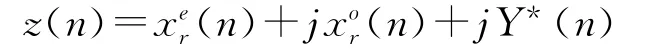
利用定理1可以得到

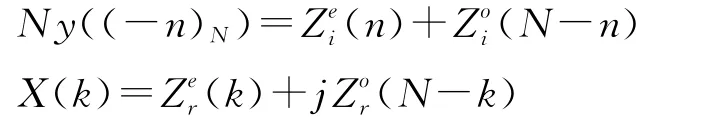
从而同时得到了y0（n）和X1（k），再计算

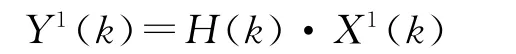
第3～（m－1）步可仿照第2步进行。

第m步不妨记x（n）＝xm－1（n），Y（k）＝Ym－2（k），y（n）＝ym－2（n），X（k）＝Xm－1（k）。根据定理1和用第2步类似的方法构造序列z（n），然后利用新公式计算可同时得到ym－2（n）和Xm－1（k），再计算

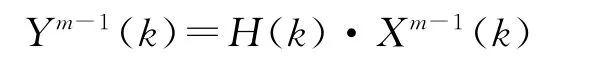
第m＋1步利用IDFT计算可得

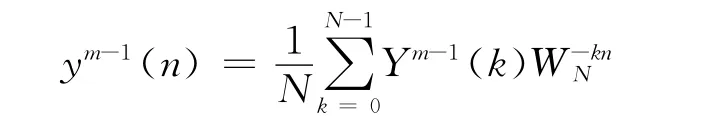
新算法到此结束。

显然，如果用上面给出的多个卷积计算的新方法来计算长度为N的m个信号通过单个滤波器的输出时，仅仅需要m个长度为N 的DFT和1个长度为N的IDFT。与传统的算法相比，减少了m－1个IDFT的计算，从而提高了计算效率。关于二维的情况与本文讨论的一维的情形类似，详细内容可参阅文献［12］。

2.4 传统和改进卷积计算方法对比分析

本数值模拟分析是在Intel P4 2.8G＋512M＋ WinXP SP2＋Visual C＋＋6.0环境下进行的，模拟数据分别为128个长度为256的实序列x［128］［256］与1个长度为256的实序列h［256］。分别采用2.2中的传统卷积计算方法和2.3中的新方法来计算128个长为256的实序列分别与1个长为256的实序列的卷积，即相当于计算128个信号通过1个滤波器的输出。用传统和改进方法进行计算的运行时间对比如表2所示。

表2 传统与改进方法运行时间对比Table 2 Contrast of the running time of the traditional and improved methods

由于软件的运行时间会受到很多因素的影响，表2中的结果是将程序反复运行多次后出现的1个较稳定的数据。从表2所示的运行时间对比来看，改进方法的运行时间大约比传统方法节约1／3，这也充分证明了将同时计算实序列的DFT和IDFT新公式应用于卷积计算确实有较大的优势。

3 结论

对于给定的X（k）和y（n）（这里y（n）是一个实序列，X（k）是另一个实序列x（n）的 DFT），Gunther（2002）给出的4组同时计算x（n）和Y（k）的直接公式中第2、4组都有错误，作者在文献［8］更正了第4组公式的基础上，改正了第2组公式中的错误，并以此公式为基础提出了一种快速计算多个卷积的新算法。

用一个复序列的DFT同时计算一个实序列的DFT和另一个实序列的DFT的IDFT的工程意义为有可能将传统数字信号处理中的编码和解码过程同时进行，从而极大地提高数字信号处理的速度。本文第2部分讨论了计算m个长为N的序列所构成的信号簇通过一个滤波器的输出问题，这是数字信号处理中的典型应用。分析结果表明，新方法能较大地减少计算量，提高计算效率。

［1］Smith W W，Smith J M.Handbook of Real－Time Fast Fourier Transform［M］.Piscataway NJ：IEEE Press，1995.

［2］蒋长锦，蒋勇.快速傅里叶交换及其C程序［M］.合肥：中国科学技术大学出版社，2004.

［3］Moshe S，Hertz D.On computing DFT of real N－point vector and IDFT of DFT－transformed real N－point vector via single DFT ［J］.IEEE Signal Processing Letters，1999，6（6）：141.

［4］Gunther Jacob H.Simultaneous DFT and IDFT of real N－point sequences ［J］.IEEE Signal Processing Letters，2002，9（8）：245－246.

［5］Sun Q，Tang Y Y.Some new explicit formulas for computing 2－D DFT of a real matrix and IDFT of 2－D DFT of another real matrix by a single 2－D DFT and their applications［J］.Journal of Sichuan University：Natural Science Edition，2000，37（6）：819－828.

［6］Liu L，Sun Q.A problem on mersenne transform over Fq2［J］.Advances in Mathematics，2004，33（4）：500－501.

［7］范安东，孙琦.同时计算二维实序列的DFT和二维实序列的DFT的IDFT的新公式［J］.成都理工大学学报：自然科学版，2007，34（6）：691－696.

［8］范安东，孙琦.同时计算实序列的DFT和IDFT的新公式及其在数字音频水印中的应用［J］.四川大学学报：工程科学版，2008，40（2）：96－100.

［9］Gasquet C，Witomski P.Fourier Analysis and Applications［M］.北京：世界图书出版公司，2005.

［10］胡广书.数字信号处理［M］.北京：清华大学出版社，2003.

［11］Yuan H，Chen H F，Yao D Z.A new general linear convolution model for fMRI data process［J］.JESTC，2005，3（1）：68－71.

［12］范安东.离散傅里叶变换及其在密码学中的应用［D］.成都：四川大学档案馆，2008.