均质储层球向渗流模型及其Laplace空间解

陈宗荣

（西昌学院 汽车与电子工程学院，四川 西昌615013）

1966年，A.T.Chatas提出当油层只打开很小的层段开采时，油藏中具有球向流动特性，并建立 了 球 向 流 动 油 藏 模 型［1］；1980 年，W.E.Brigham等分析了考虑井筒储集的球向流动油藏［2］；1985年，J.A.Joseph和 L.F.Koederitz又进一步研究了考虑井筒储集和表皮效应球向流动问题。现实问题中有许多情况采用球面向心流（简称球向流）模型进行试井分析更合适，例如存在底水或者块状厚油层试井、电缆式地层试井、垂向干扰试井等情形［3］。

2001年以来，国内一些学者兴起了油藏中储层及井底压力分布式的相似结构［4－12］研究，获得了大量卓有成效的结果，其主要结论是：某些渗流模型解的表达式具有相似的结构——可以表示为连分式或连分式的乘积形式，且结构形式只与某一边值条件有关，而其所谓的相似核函数与定解方程和另外的边值条件有关。但以前有关相似结构的研究并未涉及到球向渗流问题。

1 球面径向渗流的数学模型

考虑具有井筒储集和表皮效应下的变流率的球面径向心渗流网络，假设：储层水平、孔隙介质均一、各向同性、产层厚度均匀、单相的流体球向流入井内；流体微可压缩（即压缩系数是常数），流体的黏度不改变且服从等温达西定律；忽略重力、毛管力的影响；开井前，油藏中各处压力均等于原始地层压力p0，开井后以变产量q（t）生产。这样，就可建立如下的分形介质球向渗流的数学模型。

渗流基本方程

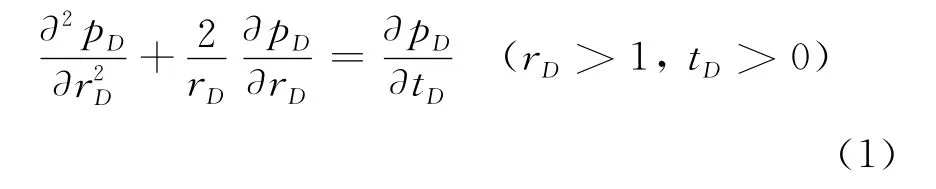
初始条件

内边界条件

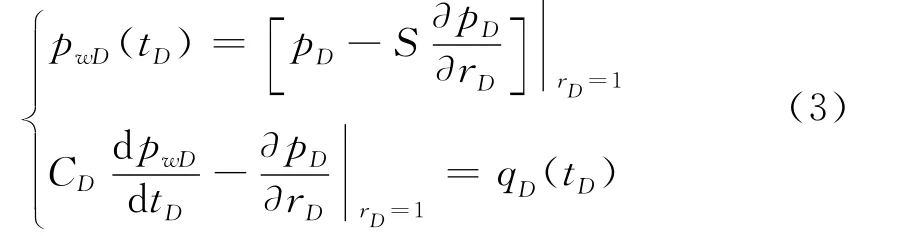
外边界条件为

这里：pD，pwD，tD，rD，RD，qD，CD分別为无量纲量储层压力、井底压力、时间、球向距离、外边界半径、流率、井筒储集系数；S为表皮因子（或称污染系数），其定义见文献［3，13，14］。

2 模型的求解及其解的相似结构

先作变换

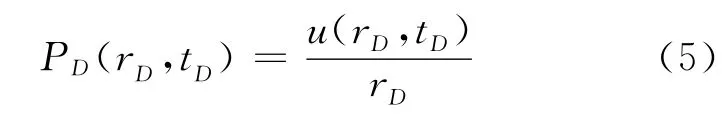
则定解问题（1）～（4）式可转化为如下简单的形式

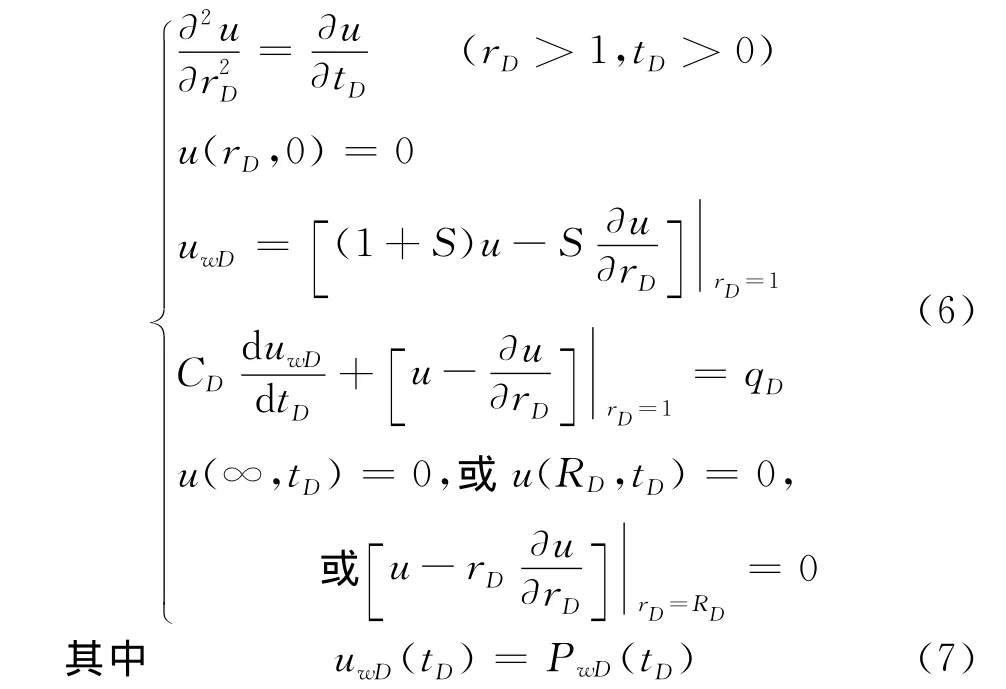
再对定解问题（6）作关于无量纲时间tD的Laplace变换（z为Laplace空间变量）

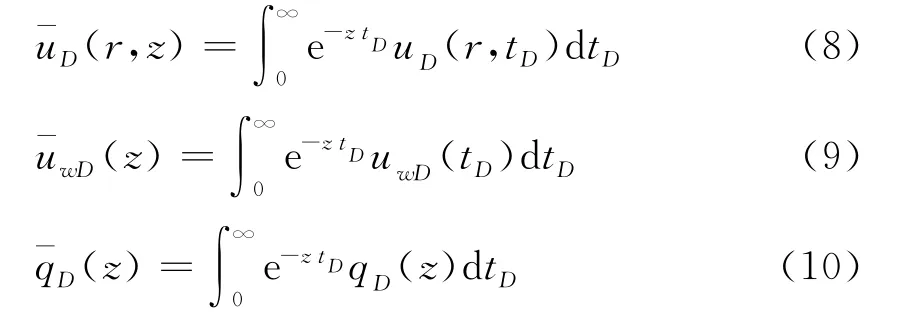
则上述定解问题（6）转化成如下的常微分方程边值问题

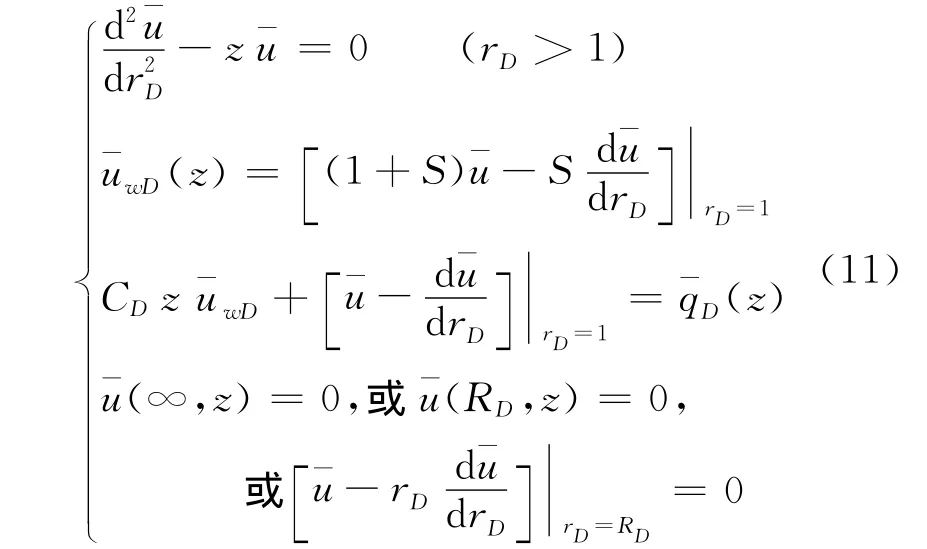
易知，（11）式中的定解方程的通解为

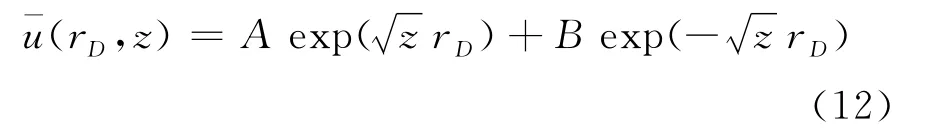
其中在求特解时，任意常数A和B由（11）式中的定解条件确定。

利用 （11）式中内边界条件，得

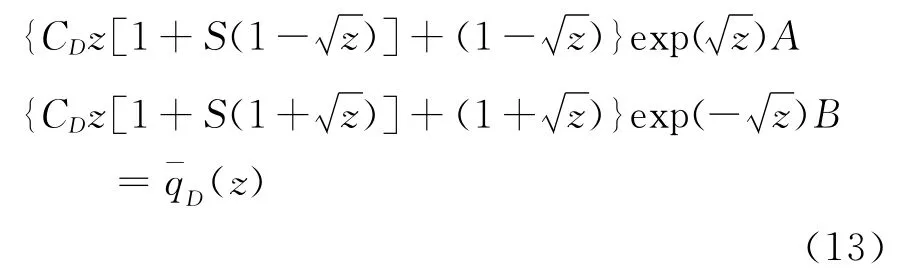
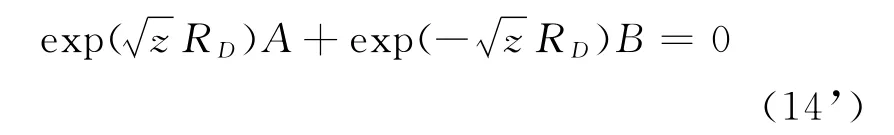
得

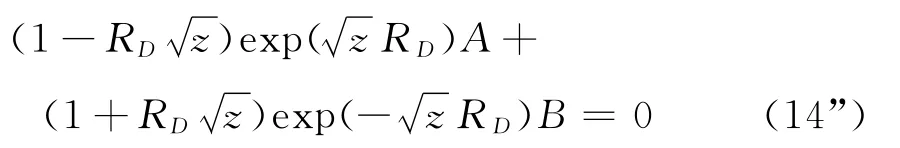
若定义相似核函数Ψ（rD，z）如下

联立求解线性方程组（13）、（14），确定待定常数A和B后，将其代入（12）式中得到再由（5）式，即得具有相似结构的储层内无量纲压力的Laplace空间解。对于3种外边界（无穷大、定压、封闭）条件，均具有统一的表迖式

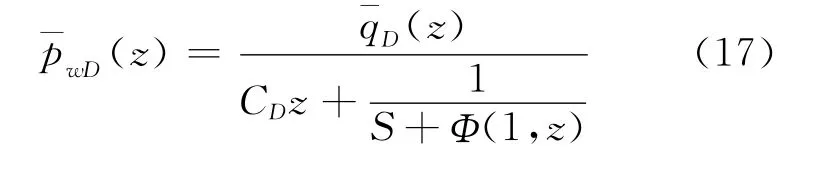
3 结论与认识

b.一般情况下，可采用Stehfest数值反演公式［15］，求得所给统一形式的表迖式（即解的相似结构式（16）式和（17）式）相对应的不同情况下的实空间数值解，完全满足试井分析中的应用需要。

c.由（15）式知，相似核函数Ψ（rD，z）只与定解方程的2个线性无关的解（或及外边界条件有关，而与内边界条件无关；而解的相似结构式，即（16）式和（17）式，只与内边界条件有关，而与外边界条件无关。这既使得内、外边界条件对储层中的压力与井底压力的影响变得十分清晰明了，无疑又给编制试井分析软件带来了极大的方便，可以简化和优化软件结构。

d.由相似结构式（16）和（17），很容易看出和分析井筒储存与表皮效应对储层压力和井底压力的影响。

［1］Chatas A T.Unsteady spherical flow in petroleum reservoir［J］.SPE Journal，1966，6（2）：102－114.

［2］Brigham W E，Peden J M，Ng K F，et al.The analysis of spherical flow with wellbore storage［J］.SPE Journal，1980，20（5）：21－29.

［3］Joseph J A，Koederitz L F.Unsteady－state spherical flow with storage and skin［J］.SPE Journal，1985，25（6）：804－822.

［4］李顺初，刘德华，张普斋.均质油藏在不同边界条件下的压力分布［J］.江汉石油学院学报，2001，23（2）：16－17.

［5］李顺初，李小平，黄炳光，等.均质储层压力动态解的综合研究［J］.钻采工艺，2002，25（1）：50－51.

［6］蒲俊，李顺初，伊良忠.外边界定压油藏中控制井底压力状态下的产率试井分析［J］.勘探地球物理进展，2004，27（6）：448－450.

［7］李顺初，郑鹏社，张宇飞.均质油气藏试井分析解的相似结构［J］.纯粹数学与应用数学，2006，22（4）：459－463.

［8］蒲俊，李顺初，伊良忠.外边界封闭储层中控制井底压力状态下的产率试井分析［C］／／数学及其应用.北京：原子能出版社，2007：545－548.

［9］李顺初，郑鹏社，张宇飞.复合油藏试井分析解的相似结构［J］.数学的实践与认识，2008，38（3）：23－28.

［10］李顺初，郑鹏社，张宇飞.合采油藏试井分析解的相似结构［J］.高校应用数学学报，2009，24（2）：234－238.

［11］李伟，李顺初，苏见朋.裂缝－洞－井连通油藏模型及其Laplace空间解［J］.钻采工艺，2009，32（5）：47－49.

［12］李顺初.微分方程解的相似结构的初探与展望［J］.西华大学学报：自然科学版，2010，29（2）：223－226.

［13］孔祥言.高等渗流力学［M］.合肥：中国科技大学出版社，1995.

［14］同登科，陈钦雷，廖新维，等.非线性渗流力学［M］.北京：石油工业出版社，2003.

［15］Horald Stehfest.Numerical inversion of Laplace transforms ［J］.Communications of the ACM，1970，13（1）：47－49.