非标准模型下的逐点可测性

陈东立，郑焕平，史艳维

(1.西安建筑科技大学理学院，西安 710055;2.西安培华学院 基础部，西安 710125)

20世纪60年代A.Robinson［1］创立了非标准分析。非标准分析是利用数理逻辑方法来探讨和刻画微积分的理论基础，为数学开辟了新的研究领域。自非标准分析创立以来，国内外许多的数学家利用非标准分析理论，对拓扑空间［2］、泛函分析、微分方程、概率论［3］、代数数论、数理经济等多方面领域做出了深入细致的研究与刻画。

连续函数是数学分析的主要研究对象，而可测函数要比连续函数内容更加丰富，应用更加广泛。测度通俗地讲就是测量几何区域的尺度。本文是在非标准模型下引入逐点可测性的概念，从而得到一些相应性质定理，并讨论了逐点可测性与Loeb可测性及泛Loeb可测性之间的关系，进而使得在饱和原理下，内函数的逐点可测性有意义且等同于一般的可测性。

设X、Y是无限集，R是实数集，V(S)是以S为个体集的超结构，V(*S)是V(S)的非标准模型，*X是X 的扩张，X⊂*X，Y⊂*Y。

定义1 设A是一个集合，Ω⊆P(A)，若对于Ω的任意有限个元素A1，A2，…，An，均有，则称集族Ω具有有限交性质。

定义2［4］设κ是无限基数，V(*S)是κ饱和的，即对于V(*S)中的任一具有有限交性质的非空内集族{At}t∈T，且 card(T)＜ κ，有特别地，如果V(*S)对于κ≥card(V(S))是κ－饱和的，则称V(*S)是多饱和的。

定义3 设X是任意集合，A是X的一个子集族，如果A满足

① X∈A。

② 对任意集A∈A，有Ac∈A。

③ 对任意有限序列A1，…，An∈A，有，则称A为X上的一个代数。

定义4 设Ai⊆P(Xi)，i=1，2是代数，则称函数 f:X1→X2关于A1和A2可测，当且仅当对所有C2∈A2，有 f－1(C2)∈A1。

在拓扑空间上可以定义逐点连续的概念:设X，Y是拓扑空间，函数f:X→Y，x∈X，如果对f(x)的任意邻域V，存在x的邻域U，使得f(U)⊆V，则称f在点x处连续，且一个函数在某一个集合上连续当且仅当它在此集合上的每一点处连续。

设X，Y是非空集合，f:X→Y，A，B是X上的代数，可类似的定义f在X上一点x处可测:若对任意B∈B，f(x)∈B，存在且x∈A，使得f(A)⊆B，则称f在x处可测。但是如此定义的“点可测”没有与通常可测性相似的性质。

定义5 设A⊆P(X)，B⊆P(Y)是代数，且 g:*X→*Y是内函数，σA={*A:A∈A}，σB={*B:B∈B}，函数g称为在点x∈*X处关于σA和σB可测，当且仅当对任意B∈B，g(x)∈*B，存在A∈A，x∈*A，使得g(*A)⊆*B。

下面此定理证明了对所有x∈*X的逐点可测性等同于通常的可测性，并且进一步等价于某给定拓扑的连续性。

定理1 设A，B分别是X，Y上的代数，对内函数g:*X→*Y下列条件等价:

(1)g是关于σA和σB可测。

(2)g是在所有点x∈*X处关于σA和σB可测。

(3)g是 T(σA)，T(σB)－连续.其中 T(σA)是包含σA 的最小拓扑，T(σB)类似。

证明

(1)⇒(3)设对任意B∈σB，只要证g－1(B)∈T(σA)即可.因为g是关于σA和σB可测，所以对所有B∈σB，有 g－1(B)∈σA，又由于σA⊆T(σA)，所以 g－1(B)∈T(σA)。

(3)⇒(2)设x∈*X，B∈B且 g(x)∈*B，因为 g在 x处是 T(σA)，T(σB)－连续，所以对任意 T∈T(σA)，存在 x∈T，使得 g(T)⊆*B，又由于σA 是 T(σA)的基，则存在*A∈σA，使得 x∈*A⊆T，所以g(*A)⊆*B。

(2)⇒(1)设 B∈B，x∈*X，g(x)∈*B，存在 Ax∈A，x∈*Ax，且 g(*Ax)⊆*B，由于g－1(*B)，且 g－1(*B)是内的，由多饱和原理，存在有限多 Axi，i=1，…，n，且，因此g－1(*B)=*A，其中，因为A是代数，所以有A∈A。

推论设A，B分别是X，Y上的代数，函数f:X→Y，则f是关于A和B可测当且仅当*f在点x∈*X处关于σA和σB可测。

证明

⇒ 因为 f是关于 A 和 B 可测，所以对 B∈B，有 f－1(B)∈A，由转换原理［5］:有*f－1(*B)∈σA，则由定理1知*f在点x处关于σA和σB可测。

⇐ 设B∈B，则对每个x∈*X，存在 Ax∈A且 x∈*Ax，使得*f(*Ax)⊆*B。由于是内的，由多饱和原理，存在有限个 Axi，i=1，…，n，且有因此*f－1(*B)=*A，其中，由转换原理得 f－1(B)=A，因为 A为代数，所以 A∈A，即f－1(B)∈A。

Loeb测度是Loeb在1975年将一个内代数上定义的内测度扩张到由这个内测度生成的σ－代数上，成为一个标准测度。

定义6［6］设(X，A，μ)是一个有限测度空间，则由转换原理(*X，*A，*μ)是一个内的，有限可加测度空间。关于(X，A，μ)的 Loeb空间定义如下:令及是P(*X)到R+∪{0}的映射，使得对任意A∈P(*X)有:

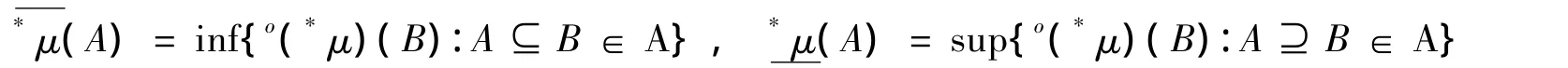
注 设Aμ是A关于μ的完备，显然有Aμ是σ－代数并且有Aμ={C⊆X，存在A，N∈A，使得A⊆C⊆A∪N，且 μ(N)=0}。

定义7 设A⊆*X，如果对所有有限内测度*μ，都有A∈L(*A，*μ)，则称A是泛Loeb可测的。所有泛Loeb可测集的集族记为Lμ(*A)=Lμ。

引理［7］设A是X上的代数，L⊆A是子族，则有

下来证明*f在点 x处对所有 x∉N是关于σA和σB可测，设 x∉N，B∈B，*f(x)∈*B，因为 x∉*NB，*f－1(*B)⊆*AB∪*NB，取 x∈*AB，由于 AB∈A，则*f(*AB)⊆*B，所以*f在点 x 处是关于σA 和σB

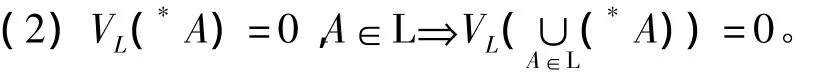
定理2 设A⊆P(X)是σ－代数，B⊆ P(Y)是代数，且μ|A是有限测度，函数f:X→Y，则有f是关于Aμ和 B 可测，当且仅当*f在点 x处关于σA 和σB 可测，其中 x∈*X，*μL－a.e..。

证明

⇒ 因为 f－1(B)∈Aμ，B∈B 则存在 AB，NB∈A，AB，⊆f－1(B)⊆AB∪NB，且 μ(NB)=0，设 N=可测。

⇐ 设B∈B，只要证C=f－1(B)∈Aμ即可。由于

则由引理及条件知*C是*μL－可测的，所以对n∈N，存在D，E∈*A，D⊆*C⊆E且*μ(E－D)＜1/n，由转换原理C∈Aμ。

设 μ 是完备测度，即 A=Aμ，则由推论和定理2知:如果*f是逐点关于σA 和σB 可测*μL－a.e..，则它是处处逐点关于σA和σB可测。特别地，定理2证明了*f的所有关于σA和σB可测点的集对关于Aμ和B可测函数f是*μL可测。然而下面此定理不需要基于Loeb测度*μL，对任意函数f和测度μ，可测点的集是μL可测的。

定理3 设 A⊆ P(X)是σ－代数，B⊆ P(Y)是代数，且对任意B∈B，都有函数f:X→Y，令F是所有点x∈*X的集使得*f在点x处关于σA和σB可测，则F是泛Loeb可测。

证明由题知，其中

由FB的定义有:

设 μ|*A是有限内测度，对每个C⊆Y 选An∈A 且f(An)⊆C，μL(*An)↑sup{μL(*A):A∈A，f(A)⊆C}，设，则 AC∈A，f(AC)⊆C。又对任意 A∈A，有 f(A)⊆C，所以

令LB={A∈A:f(A)⊆B或，由式(1)与(2)可得

由式(3)对任意 B∈B，A∈LB，取，因此由引理有 μL(N)=0。设 D=，则由引理知，D是μL可测。由于F－D⊆N且μL(N)=0，F－D也是μL可测的，因此F=D∪(F－D)是μL可测的。

［1］Davis M.Applied nonstandard analysis［M］.New York:Wiley，1977.

［2］陈东立，马春晖，史艳维.拓扑的非标准定义［J］.西北大学学报:自然科学版，2006，36(3):348－350.

［3］Loeb P A.Conversion from nonstandard to standard measure spaces and applications in probability theory［J］.Trans.Amer.Math.soc.，1975，211:113 －122.

［4］Cutland N J.Nonstandard measure theory and its applications［J］.Bull London Math Soc，1983，15:529 －589.

［5］Anderson R M.Star-finite representations of measure spaces［J］.Trans Amer Math Soc，1982，271:667 －687.

［6］Chen Dongli.The Loeb Space of Denumerable Infinite Dimensional Probability Product Measure Spaces［J］.Northeast Math J，2003，19(3):249 －253.

［7］Landers D，Rogge L.Universal Loeb-measurability of sets and of the standard part map with applications［J］.Trans Amer Math Soc，1987，304:229－243. (责任编辑刘 舸)