LFM发生器及其在超声波TDOA测量中的应用

鲍正祥，李洪海，赵正敏

(1.淮安信息职业技术学院，江苏 淮安 223003;2.淮阴工学院电子与电气工程学院，江苏 淮安 223003)

0 引言

超声波信号TDOA(Time Delay Of Arrival)或TOF(Time of Flight)的相关估计中，LFM(Linear Frequency Modulation)信号是一种简单有效的激励信号。尽管LFM信号不像PRBS及混沌信号一样可以很好地克服Cross－talking，但它不需要调制，可以基带传输，不仅传输效率高，而且相关函数的主副瓣幅度差别明显，所以在单组超声波传感器应用中经常采用，但大功率高频正弦驱动较难实现。事实上，超声波发生器可以看成一个中心频率为其特征频率的带通滤波器，可以采用离散方波LFM(Digital Rectangular LFM－DRLFM)驱动，不仅可以实现大功率驱动，利用文献［7］提出的递推算法，还可以进一步提高其计算速度。

DRLFM可以通过将正弦LFM信号和参考信号进行比较获得，但对基于可编程器件的DDFS来说，这并不是唯一的方法。在可编程器件中，高速数字比较器不仅易于实现与调试，而且性能稳定可靠。本文介绍一种基于DDFS的全数字DRLFM的产生电路，比较正弦LFM信号与离散方波LFM的相关函数及频谱特性，分析DRLFM用于TDOA估计的可行性，介绍信号产生电路结构及通过可编程器件实现的方法，最后通过实验验证方案的可行性。

1 TDOA估计中LFM激励信号

1.1 基于超声波激励的TDOA估计

以直射式超声波发射与接收器件组为例，分析超声波传输过程及其TDOA估计。超声波信号传输一般包含超声波换能器激励、超声波传输及超声波信号拾取等过程，其传输过程可以用图1所示的模型描述。

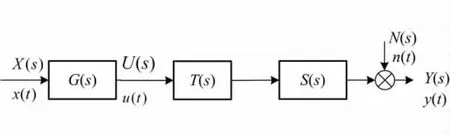
图1 TDOA估计中超声波信号的传输

图1中，x(t)是激励信号，u(t)是超声波换能器输出信号，传感器的输出信号为y(t)，系统中的其它噪声用n(t)表示。G(s)、S(s)、T(s)分别是超声波发生器与接收器及传输介质的传递函数，X(s)、U(s)、N(s)和Y(s)分别为上述各信号的频域表示。显然，

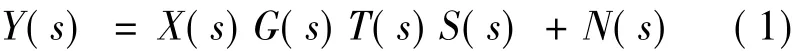
由于超声波传输可以看成是无畸变传输。即T(s)=Ke－Tds，K 是增益，Td是信号传输时间，所以(1)式可以写为，

1.2 DRLFM的自相关函数及频谱

从上文可以看出，要想稳定可靠地测量TDOA，激励信号的互相关函数主副瓣幅度的差别必须很明显，且信号的带宽要尽量在超声波器件的通带范围内。图2、图3分别是连续的正弦LFM和DRLFM的相关函数，采样频率fs=8f0。从图中可以看出，DRLFM在相关函数及频谱上和正弦LFM信号很相似，离散化处理对信号的频谱及相关函数并无多大影响。

图2 LFM自相关函数及其频谱

图3 离散LFM自相关函数及其频谱

2 基于可编程器件的DRLFM发生器

2.1 电路结构及工作原理

图4是采用可编程器件实现的DRLFM信号发生器框图，系统主时钟频率为fCLK。在每个时钟周期中，频率变化率和频率控制字累加一次，实现频率的线性增加，频率控制字FW的初值为FW0，相位累加器PA与N位频率控制字FW累加一次，实现相位的调频变化。

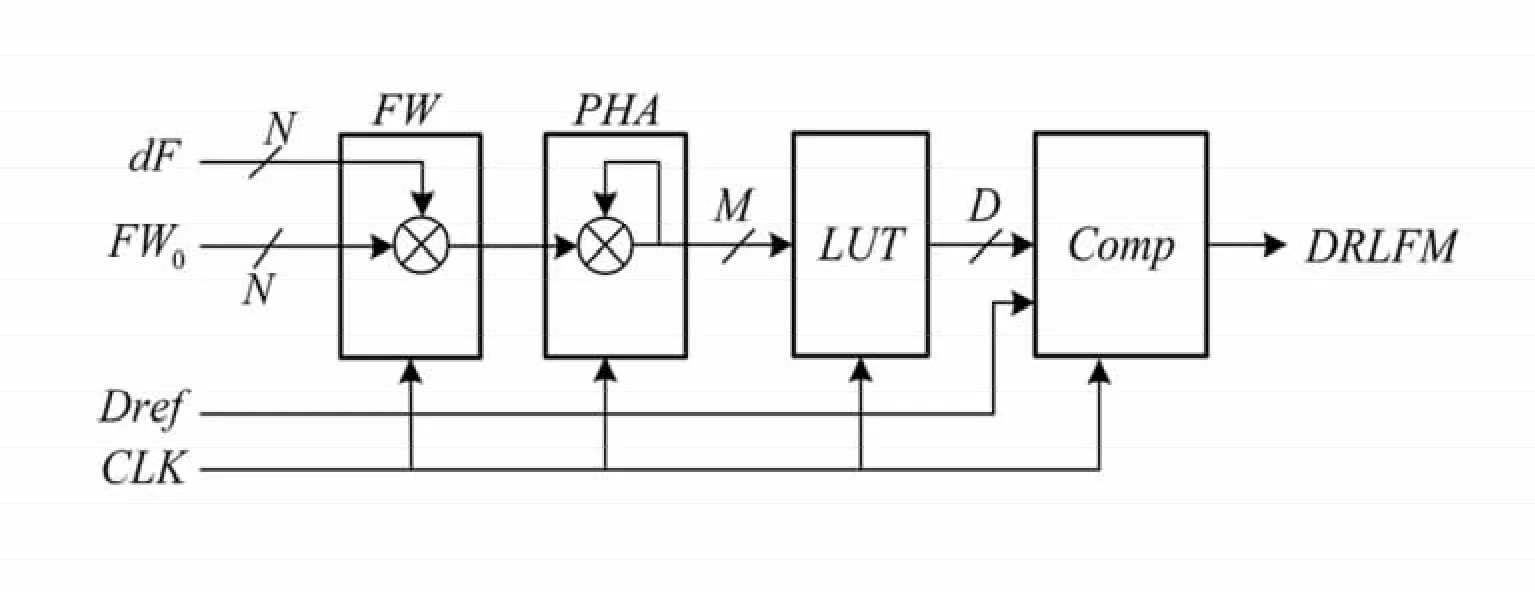
图4 全数字DRLFM发生器

N位相位累加器的高M位作为LUT(Look－Up－Table)地址，LUT中存放的D位的正弦信号波形数据在M位地址信号的寻址后输出，送至数字比较器Comp与给定的参考信号Dref进行比较，产生方波信号。其调谐方程为，分辨率为df

根据超声波换能器的中心频率f0、带宽BW和信号持续时间△t，可以确定DRLFM的起始频率控制字为调频速度dF =

通过改变FW可以调节DRLFM的中心频率;通过设定dF可以设定调频速度，当dF=0时，输出为频率稳定的方波信号;通过改变参考电压数据Dref，可以调节方波的占空比。

2.2 参数选择与计算

本文以中心频率为1MHz的防水型超声波发送与接收对为例，选择并计算DRLFM的相关参数。N=40，M=10，D=8，相位累加器采用流水线结构，LUT中的四分之一象限的正弦波形数据为256字节，可以在FPGA或CPLD内部实现。Comp为8位比较器。

当 fCLK=80MHz，df=7.275957614183426 ×10－5Hz，超声波换能器的中心频率f0=1MHz、带宽BW=0.2MHz，信号持续时间 △t=1ms，可以确定DRLFM的起始频率控制字FW0=(f0－BW/2)/df≈(12369505812)D;DF=相对误差小于0.01%。

和其它的DDFS电路一样，当频率控制字为非2的整数幂时，输出信号中会产生轻微的相位截尾误差，但当fCLK很高时，这种相位抖动远小于模拟比较器及模拟信号中的干扰。本系统中采用的是MAX II，该器件最高工作频率可达300MHz。此外，由于采用相关估计算法估计TDOA，适当的相位抖动对相关估计的精度是有益的。

2.3 DRLFM发生器的特点

2.3.1 全数字结构

图5是采用常规的相位累加型正弦波DDS和高速比较器构成的DRLFM发生器。和图5的方案相比，我们设计的基于DDFS的DRLFM产生电路，省去了高速DAC电路和高速比较电路，实现了电路的全数字化，电路简单，且易于调试与控制。

图5 基于DDFS的DRLFM发生器

2.3.2 精度高

一方面，由于采用了全数字结构，减少了外部干扰信号对电路的影响，特别是对其中DAC、比较器等电路中模拟信号的干扰。因此，系统精度及稳定性取决于所用的晶体振荡器。另一方面，DDFS内在高精度、高分辨率也保证了所设计的DRLFM信号发生器的精度与分辨率。对于中心频率为1MHz的防水型超声波换能器来说，其频率精度是满足要求的。

2.4 实验结果

为了验证这种方法的正确性及可行性，我们采用中心频率为1MHz、带宽为0.2MHz的防水型超声波传感组作为试验传感器，并以MAX II器件EPF1270T144C3构成上述基于DDFS的DRLFM电路及超声波 TDOA实验系统。本实验中，f0=1MHz，初始频率为 0.9MHz，y(n) 为采集信号，采样频率为fs=Ksf0=20Msps。图6是一组采用正弦LFM激励的测量结果。

图6 超声波TDOA的估计实验结果

图7是一组采用DRLFM激励的测量结果。其中，TDOA=33.57us。

图7 超声波TDOA的估计实验结果

3 结论

本文提出基于DDFS的全数字DRLFM信号发生器，省去了DAC电路及模拟比较电路，电路结构简单，易于FPGA或CPLD的硬件实现。由于没有模拟电路，电路受外部电磁干扰的可能性也大大降低，因此频率稳定，相位抖动小，所产生的方波信号也易于驱动，用于超声波TDOA的估计，不仅可以递推计算其相关函数，还可采用基带传输，相关函数主瓣也较窄，从而提高了算法的精度、改善了鲁棒性。这种电路为高频、高精度超声波测量提供了一种有效的驱动信号产生方法。

［1］Grennberg A，M Sandell.Estimation of subsample time delay differences in narrowband ultrasonic echoes using the Hilbert transform correlation［J］.Ultrasonics，Ferroelectrics and Frequency Control IEEE Transactions on，1994，41(5):588－595.

［2］Marioli D，Narduzzi C，Offelli C，et al.Digital time－ offlight measurement for ultrasonic sensors［J］.Instrumentation and Measurement IEEE Transactions on，1992，41(1):93－97.

［3］Pollakowski M，H Ermert.Chirp Signal Matching and Signal Power Optimization in Pulse－Echo Mode Ultrasonic Nondestructive Testing［J］.Ultrasonics Ferroelectrics and Frequency Control，IEEE Transactions on 1994，41(5):655－670.

［4］程晓畅，苏绍景，王跃科，等.伪随机码超声扩频测距系统设计与算法［J］.测试技术学报，2007，21(1):79－84.

［5］Yao Zhenjing，Meng Qinghao，Li Genwang.Non－Crosstalk Real－Time Ultrasonic Range System with Optimized Chaotic Pulse Position－Width Modulation Excitation:IUS 2008:Ultrasonics Symposium，2008，Beijing，Nov.2－ 5，2008［C］.Washington:IEEE International Conference on，2008.

［6］Hirata S，M K Kurosawa，T Katagiri.Real－ time ultrasonic distance measurements for autonomous mobile robots using cross correlation by single－bit signal processing:ICRA ＇09:Robotics and Automation，2009，Kobe，May 12－17，2009［C］.Washington:IEEE International Conference on，2009.

［7］赵正敏，李洪海.超声波TOF的递推相关估计［J］.仪器仪表学报，2010，31(12):2689－2694.

［8］葛万成.相关法高抗干扰超声波距离测量中的信号处理［J］.同济大学学报，2002，30(1):71－77.

［9］赵正敏.DDS流水线结构的改进［J］.电子技术应用，2001，27(3):56－58.

［10］赵正敏.相位截尾对DDS输出频谱影响的分析与计算［J］.东南大学学报:自然科学版，2000，30(1):141－145.