数控珩磨机进给系统模糊神经网络控制研究
2011-07-03孙珍菊赵家黎杨宁都
孙珍菊,赵家黎,杨宁都,龚 俊
(兰州理工大学 机电学院,兰州 730050)
0 引言
目前,高档数控珩磨机的进给系统主要是通过比例阀来控制进给压力和进给位置的,但是液压系统具有非线性、扰动性且比例阀具有零位死区,使控制相对滞后、不稳定。因此,如何实现珩磨机进给系统快速、平稳的响应是一个亟待解决的问题。
模糊神经网络(Fuzzy neural network,FNN)结合了神经网络自学习、自适应强的特点和模糊推理性强的优点,成为近年来研究的热点[1]。数控珩磨机进给系统的模糊神经网络控制器,是利用模糊推理来训练神经网络,在神经网络进行学习时运用BP算法来修正网络参数。这两者的结合对于复杂多变量系统,有助于提高学习速度和控制精度。
加工时采用在线气动测量磨头进给位置和油石涨出压力来不断的改变比例减压阀、比例换向阀的电压值,从而达到多级进给,实现珩磨机的随动进给。

图1 进给系统液压原理图
1 数控珩磨机进给运动原理及建模
1.1 进给运动原理
珩磨加工包括粗珩、精珩和光整加工三个过程[2],进给运动是珩磨加工过程中不可缺少的主要运动之一。
如图1所示,从小泵输出的压力油,经二位三通电磁阀分别进入高、低压比例减压阀,获得两级压力后进入三位四通比例换向阀。粗珩时,粗珩油缸活塞下移,通过连杆推动珩磨头粗珩锥体下移,实现粗珩进给;精珩时,精珩油缸下移,通过连杆推动精珩锥体下移实现精珩进给。珩磨
1.2 珩磨机进给系统阀控缸数学模型
数控珩磨机进给系统多级压力控制是通过比例减压阀来实现的,比例减压阀的功能是降压和稳压,并能提供压力随输入电信号变化的恒压源。
数控珩磨机不同位置下比例减压阀控制油石涨出压力,是实现精确随动进给的关键[3]。以比例减压阀为主要研究对象,建立珩磨机进给系统具有动态压力反馈的位置的传递函数[2],其框图如图2所示。

图2 比例阀控液压缸传递函数框图
其中,v—比例减压阀的固有频率,rad/s;
v—比例减压阀阻尼系数;
Ap—液压缸活塞有效面积,cm2;
h—液压缸固有频率,rad/s;
h—液压缸阻尼系数;
m—外负载质量,kg;
Kfp—流量—压力系数;
Kr—传感器的位移/电压转换系数,V/m;
Ka—位移放大器增益,m/V;
Ku—电压放大器增益,I/V。
2 模糊神经网络控制器(FNNC)的设计
2.1 FNNC的结构
珩磨机进给系统是一个两输入,一输出的系统,输入量:位置误差e、误差变化率ec;输出量:控制电压u。任意调节一个变量,其它变量都要发生变化,且不具备线性关系,因此这里采用基于误差反向传播的FNN来进行控制[4]。具体控制框图如图3所示。

图3 进给系统控制结构图
2.2 模糊推理规则的确定
模糊推理采取Mamdani推理模型[5],其形式如下:
Rl:If e isand ec isThen u isC1
其中,e是进给偏差,ec是偏差变化率,u是控制输出。输入量e、ec经模糊化得到模糊量E和EC。经规则近似推理后得到模糊控制输出量U,经反模糊化得到清晰控制电压u控制比例阀动作。取 E、EC、U 的离散量化论域均为 {-6,-4,-2,0,2,4,6}。且在E、EC、U的论域上定义7个语言变量值{NB,NM,NS,ZO,PS,PM,PB},依据经验这里模糊隶属度函数应用高斯函数[6]。
模糊控制器控制规则的设计原则[7]是使系统输出相应的动态性能与稳态性能达到最佳。即当误差较大时,选择控制量以尽快消除误差为主.而误差较小时,选择控制量以防止超调,主要考虑系统的稳定性。根据控制经验,将控制过程中将出现的各种情况及相应的控制策略进行分析汇总,可得到49条控制规则,用“IF-THEN”的语句形式加以描述,部分条件语句如下:
1)If e is NB and ec is NB,then u is PB.
2)If e is NB and ec is NM,then u is PB.
…
49) If e is PB and ec is PB,then u is NB.
2.3 FNN的拓扑结构
该FNN共5层,各层的输入输出关系如下:记层n的第i个节点的输人为netn,i,输出为On,i,并且这里的同一层结点具有相同的函数。
层1:输入层。 net1,1= e,net1,2= ec;
层2:模糊化层。O2,i=Ai(net1,1),i=l,…,7,
所用的隶属函数为高斯函数;
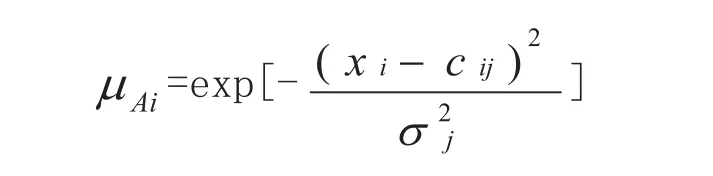
层3:规则层。这一层是固定结点,它首先作所有输入信号的积,并归一化激励强度;

其中:i=Ai(e)Bj(ec),j=1, …,7
层4:输出隶属函数层。
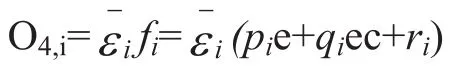
其中{pi,qi,ri}是该节点的可调线性参数集;
层5:输出层。该层只有一个节点。


图4 模糊神经网络拓扑结构
2.4 FNN的学习算法
各层之间的连接权值W和隶属函数的中心宽度j、中心值Cij是FNN需要学习的主要参数。在该系统中用误差反向传播的BP算法,调整网络参数优化网络性能,以使网络的实际输出值与期望值的误差最小[8]。当误差训练的足够小,达到控制要求时,认为此时FNN的输出是可信的,整个学习训练工作就结束[9]。
定义该FNN性能指标参数是:
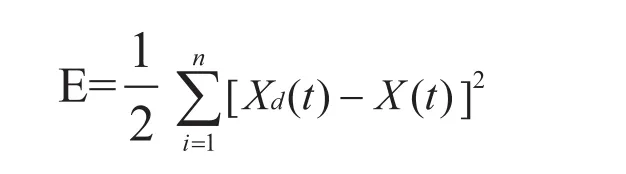
其中,n为采样个数,Xd(t)为期望输出,X(t)为系统实际输出。
网络权值的学习规则[10]为:
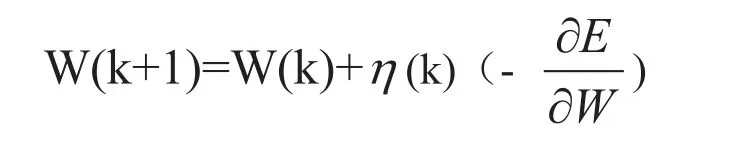
其中, 为学习率。
3 仿真分析
珩磨机进给系统的仿真参数如表1所示。

表1 珩磨机进给系统的仿真参数
选定系统控制偏差E、偏差变化EC及控制作用U的离散论域为[-6,6],实测偏差和偏差变化率的范围分别为 [-10cm,+10cm]、[-3cm/s,+3cm/s],控制输出的范围[12V,36V]。
在线测量珩磨机进给系统进给位置和控制电压数据160组,并进行数据分组处理。在MATLAB7.0环境下用M语言编写模糊神经网训练程序[10],设定训练误差10-4,经过885次训练后误差ε达0.0000991862。如图5所示。
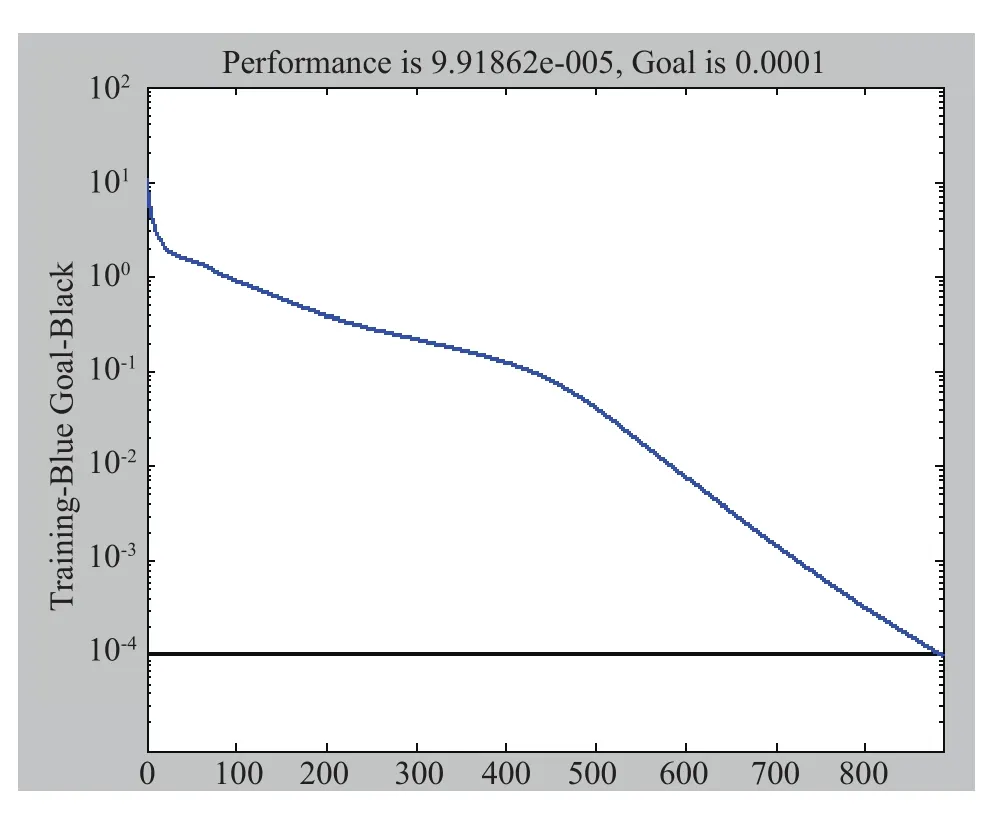
图5 模糊神经网络训练误差曲线
在SIMULINK中,以阶跃信号作为激励信号,建立珩磨机进给系统仿真模块图,将训练好的FNNC导入SIMULINK中,调整相应的仿真步长,得到图6所示仿真曲线。 从图6可以看出应用模糊控制器来控制珩磨机的进给位置时,有明显地振动、超调量大、系统4.5s才达到稳定。用FNNC来控制进给位置时,响应快速只需1.6s就达到稳定、超调量小,系统稳定性明显得到改善,综合性能优于模糊控制器。
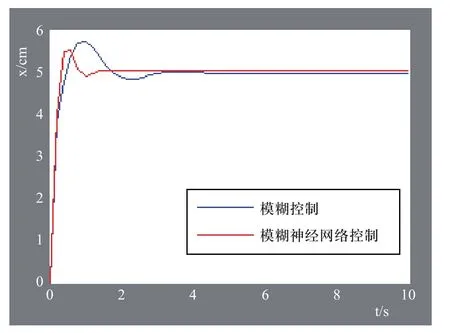
图6 仿真曲线
4 结论
1)模糊控制过于依赖专家经验,主观因素起决定作用,所以控制不精确;神经网络具有在线学习的功能,但是学习的输入/输出关系无法用直观的方法表示出来,将模糊推理与神经网络的自学习功能结合起来是一种较理想的方法。
2)仿真实验表明,本文设计的数控珩磨机进给系统模糊神经网络控制器是可行的。方法着眼于建立位置与电压之间的对应关系,可在加工过程中,在线测得进给位置,确定该位置下的油石涨出压力,实现在线随动进给。
3)本文的数控珩磨机进给系统数学模型,仅在采用比例减压阀控制油石涨出压力的况下适用,对其他形式的阀要做进一步扩展研究。
[1] 李国勇.智能控制及MATLAB实现[M].北京: 电子工业出版社, 2005.
[2] 张云电.现代珩磨技术[M].北京: 科学出版社, 2007.
[3] 陆永耕.高精度数控珩磨机控制精度设计[J].上海电机学院学报, 2009, 12(2): 95-98.
[4] 关景泰.机电液控制技术[M].上海: 同济大学出版社,2003.
[5] 张锦华, 原思聪, 等.基于模糊神经网络振动磨机控制系统研究[J].煤矿机械2011, 32(2): 141-142.
[6] 王士同.神经模糊系统及其应用[M].北京: 北京航空航天大学出版社, 1998.
[7] 蔡自兴.智能控制[M].北京: 国防工业出版社, 1998.
[8] 姜立标, 王薇, 等.半主动空气悬架模糊神经网络控制[J].哈尔滨工业大学学报, 2005, 37(12): 1747-1750.
[9] 刘增良, 刘有才.模糊逻辑与神经网络[M].北京: 北京航空航天大学出版社, 1996.
[10] 董长虹. Matlab神经网络与应用[M].
