高压高产天然气井管柱疲劳寿命预测模型研究
2011-07-03蒋德平任连城
吴 睿,蒋德平,任连城
(重庆科技学院 重庆 401331)
0 引言
高压、高产且含H2S等具有强腐蚀性气体的天然气井管柱的失效不仅影响生产的正常进行,而且会带来重大经济损失。气井管柱深埋地下,工作环境复杂且不易监测,对管柱疲劳寿命的研究不仅直接关系到管道检测、维修、更换周期的确定,而且也是延长管道寿命,降低维修费用,保证气井井口装置安全运行的需要。因此,建立管柱疲劳寿命预测模型,从而预测其剩余寿命,是一项非常重要的工作,具有广阔的应用前景。
1 天然气井管柱的腐蚀
腐蚀是引起天然气井管柱失效的主要因素。在腐蚀介质中CO2、H2S是主要的腐蚀剂,H2O是载体[1]。其中CO2引起的台面状坑点腐蚀是腐蚀过程中最严重的情况,其穿透力通常每年可达数毫米[2]。研究表明,CO2腐蚀可以由(1)式表示[3]:

式中:v——腐蚀速度,mm/a;
T——温度,℃;
Pco2——CO2分压,MPa。
式(1)表明,管柱腐蚀速度与CO2分压和温度有关。因此,欲计算腐蚀速度,应首先计算气井管柱内的温度和压力分布。
根据管柱内气体流动质量守恒、动量守恒、能量守恒和气体状态方程进行推导,可以得到如下方程组[4]:

对方程组(2),以井口处的压力p0、温度T0、密度ρ0和速度v0作为边界条件,将p、T、ρ和v记为yi(i=1,2,3,4),相应的方程记为 Fi,则方程组(2)有如下形式:

其中i=1,2,3,4
将边界条件作为初值,取步长为h,用四阶龙格一库塔法对式(3)进行迭代求解,则有:

i=1,2,3,4,k为迭代步数。
解方程组(2)可以得到气井管柱内的温度和压力分布,并根据得到的压力进一步得到CO2分压。本文关心的是气井管柱的疲劳寿命,根据气井管柱内流动规律,在接箍处由于管柱截面的突变和存在联结缝隙,存在腐蚀载体水留存的条件,腐蚀最为严重,是管柱薄弱处。此外,相关文献指出[3,5],当CO2分压大于 0.2MPa和温度在70℃- 80℃之间时,CO2的腐蚀最严重。因此,计算过程中应取满足最大腐蚀条件的接箍处作为样本点。如某气井满足上述条件的接箍数为3,则根据式(1)和方程组(2)可得到表1所示样本点计算结果。

表1 样本点计算结果
2 气井管柱疲劳寿命模型
得到表1数据后,计算出由于腐蚀导致联接管螺纹强度降低使得其强度恰好可以支持接箍以下部分总载荷(主要为管柱自身重量引起的重力,考虑高压气体流动导致的振动影响,可以乘上一个保险系数如1.2)的时间,而其中的最短时间即为气井管柱疲劳寿命。式(4)[6,7]为管螺纹强度校核公式:

其中 F——螺纹所受的轴向总载荷,N;
d0——螺纹小径,mm;
b——螺纹牙根部的宽度,mm;
z——实际工作的螺纹牙圈数;
[τ]——许用剪应力,MPa。
根据(4)式,当轴向总载荷Q为保险系数1.2乘管柱自身引起的重力时,则可以得到最小工作的螺纹牙圈数(本文称之临界圈数,以zl表示):

其中
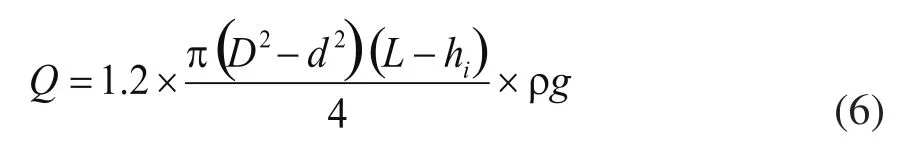
d和D为管柱内外径,(L-hi)为表1中某个接箍以下管柱高度。
将腐蚀因素加以考虑,为简化处理,假设腐蚀只引起螺纹牙根部宽度的变化,将式(4)改写为如下形式:

Δbi为腐蚀引起的第i圈螺纹牙根部的宽度的减小量。令C代表总腐蚀量,则(vi为表总计算出的腐蚀速度),进一步对式(7)进行处理,并利用式(5),则得到螺纹牙圈数z的表达式(8):
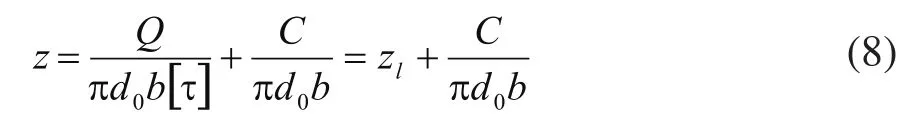
式(8)表明,当受到腐蚀后,如果要支持管柱自身产生的重力,须有更多的螺纹牙圈数参与。当z增大到联接管螺纹牙的最多啮合圈数zmax时,在该接箍处即达到使用寿命。
根据上述分析,可以得到表1中各接箍处疲劳寿命计算公式(9):

则管柱的疲劳寿命t = min{ti}。
3 结束语
本文通过天然气管柱疲劳寿命的研究,根据管柱的腐蚀和材料的剪切强度校核公式推导了管柱疲劳寿命的数值计算模型,为实际生产过程中管柱的维修、更换提供了参考依据。
[1] 任呈强.N80油钢管在含CO2/H2S高温高压两相介质中的电化学腐蚀行为及缓蚀机理研究[D].西北工业大学,2003.
[2] 何鲜.国外深曾气藏开采技术的[M].石油工业出版社,2001.
[3] 刘晓军.CO2腐蚀问题的再思考[J].小型油气藏,2006,11(4).
[4] 郭春秋,李颖川.气井压力温度预测综合数值模拟[J].石油学报,2001,22(3).
[5] De Waard C and Lotz U.Prediction of CO2Corrosion of Carbon Stee1.A Working Party Report on Prediction CO2Corrosion in Oil and Gas Industry,1994.
[6] 陈军,房玉胜.井用管螺纹的失效分析与防范[J].机械研究与应用,2005,18(5).
[7] 谢文献,颜廷俊.油管螺纹滑脱失效计算分析[J].油气田地面工程,2004,23(8).
