模糊—重复学习复合控制策略在并联型有源滤波器中的应用

王 盼 刘 飞

（1.武汉电力职业技术学院2.武汉大学电气工程学院 武汉 430072）

1 引言

近年来，由于电力电子装置的广泛应用，使得电网中电压和电流波形严重畸变，谐波所造成的危害也日趋严重。有源电力滤波器（APF）作为一种治理电网谐波、改善电能质量的有效设备，目前已成为研究热点。

由于APF的补偿电流主要是由各种基波倍频次谐波组成，故要实现无静差的快速跟踪，高性能的电流控制策略便成了决定 APF补偿性能的关键技术之一。考虑到有源电力滤波器的参考信号是多个频率叠加在一起的周期性信号，传统的PI调节器带宽有限，并不能完全无静差地跟踪快速变化的误差电流[10-13]。近年来，又提出了许多新的脉冲宽度调制（PWM）技术，如单周控制、神经网络控制、重复学习控制以及模糊控制等。其中，单周控制的控制电路简单，不需要参考信号，但容易受外界条件的影响[12]。神经网络控制则受制于它的实现技术，目前仍主要依赖串行处理器模拟实现[10]。重复学习控制是一种智能控制，它对于周期性信号和干扰具有很好的跟踪效果和抑制作用[13]。故对应于 APF的周期性特性，它能够消除所有包含在稳定闭环内的周期性误差，但也仅适用于稳定周期重复状态，倘若系统处于自身调整阶段，势必影响重复学习控制效果，情况恶劣时更会影响系统稳定性。实际运行中，系统模型往往不能精确获得，当外部系统参数发生变化时，如何选取控制参数以保证系统稳定？模糊控制的最大优点即不依赖被控对象的精确数学模型，能够克服非线性因素的影响，对调节对象的参数变化具有较强的鲁棒性，可以很好地抑制超调，比较适合强非线性、强不稳定性的系统[9]。故利用模糊控制对重复学习控制器的参数进行调节具有重要意义。

本文基于LCL滤波器的有源电力滤波器，通过理论分析详细建立了重复学习控制参数的模糊控制规则，并对模糊—重复复合控制策略下的APF稳定性及补偿性能进行了仿真验证。仿真结果证明了本文所述复合控制策略的正确性和有效性。

2 APF原理分析

并联型有源滤波器主电路由电压型三相桥式逆变器和输出滤波器组成，控制系统由谐波检测环节、电流跟踪控制器组成，将检测到的系统谐波电流ish，形成PWM逆变器所需的参考电压分量，逆变器输出经滤波器并入电网，实现谐波补偿目的[1]。其系统结构框图如图1所示。

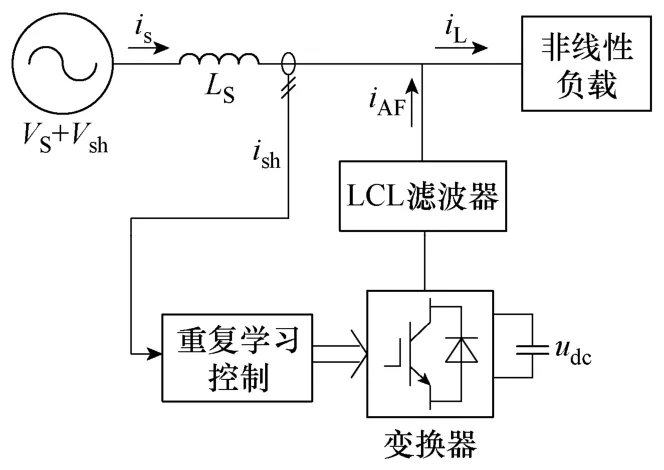
图1 基于LCL滤波器的APF系统结构框图Fig.1 Block diagram of APF based on LCL filer configuration system

通常，采用LCL滤波器时，需要加入阻尼电阻，以避免发生电流谐振，一般取值为谐振点电容阻抗的三分之一。但是，此时的阻尼系数比较低,，难以抑制低次谐波的振荡。倘若增大电阻值，虽可以提高系统阻尼, 但同时亦增加了损耗。故本文采用引入电容电流反馈的控制策略,代替阻尼电阻的作用。其显著特点是：不需要改变系统谐振频率, 同时增强了阻尼作用，有效地抑制了低次谐波的振荡[2]。图2为引入电容电流反馈环节的LCL滤波器结构图及原理图。可得其传递函数为

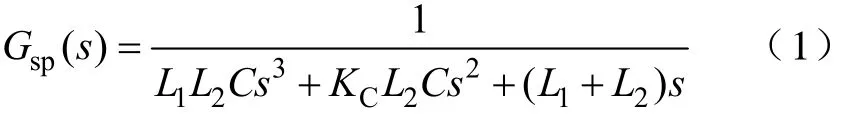
式中，KC为电容电流反馈系数；ui为逆变器侧电压，us为系统侧电压；i2为APF向系统补偿的电流。

文献[2]从系统的控制性能方面分析了，引入电容电流反馈可加快控制系统的响应速度，有利于系统稳定。

图2 引入电容电流反馈环节的LCL滤波器Fig.2 LCL filter introduced capacitance current feedback

3 复合控制策略设计

3.1 重复学习控制

重复学习控制是一种基于内模原理的控制方法，其核心是对传统重复控制的改进。图3为采用前馈—反馈混合型重复学习控制原理图，虚线框内为重复环。

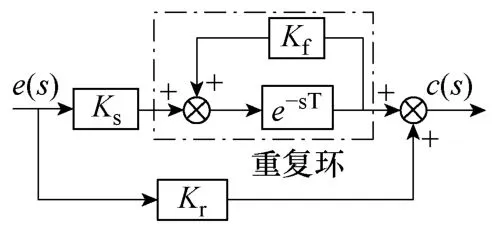
图3 重复学习控制原理图Fig.3 Block diagram of repetitive learning control strategy

图3中，e-sT表示学习周期的延时算子，T为工频周期。Kf为遗忘因子，前馈控制采用带遗忘因子的P型学习率，定义为学习因子Ks，反馈控制采用最简单的比例控制，定义为比例控制系数Kr。其传递函数表达式为

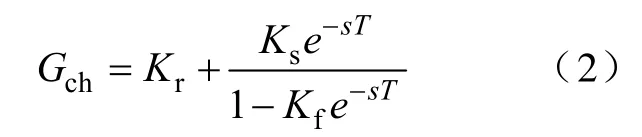
假设遗忘因子Kf=1时，重复环可视为以周期为步长的纯积分环节。此时理论上虽可实现系统的无静差，但却使系统呈现临界振荡状态，对稳定性和鲁棒性不利。因此目前实际系统通常取Kf为略小于1的常数以减弱积分效果。

3.2 模糊（Fuzzy）控制

模糊控制是一种语言控制，其原理是将来自于传感器的实时信号模糊化后输入到由操作人员或专家经验建立的模糊规则中，完成模糊推理，进而将输出量加入到执行器上[14]。图4为模糊控制器的基本原理框图，其组成一般有模糊化、模糊推理及反模糊化三部分。

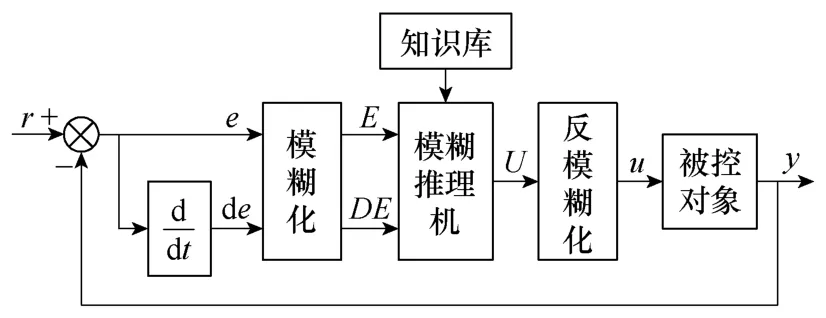
图4 模糊控制的基本框图Fig.4 The basic block diagram of fuzzy control

考虑到经典模糊控制直接面对控制对象，控制器本身消除系统稳态误差的性能比较差，难以达到较高的控制精度，所以很难直接应用于有源滤波器中。本文设计的复合控制器中，模糊控制策略用于对重复学习控制中的Kr、Ks参数进行调节，实际起主要控制作用的还是重复学习控制器。这样就能在保证系统控制精度的同时，实现对其参数的实时调整。

3.3 模糊—重复学习复合控制

图5为加入模糊控制的重复学习控制器结构框图，控制器的输入为谐波指令偏差e以及偏差变化率de，输出为控制量的调整值ΔKr及ΔKs。

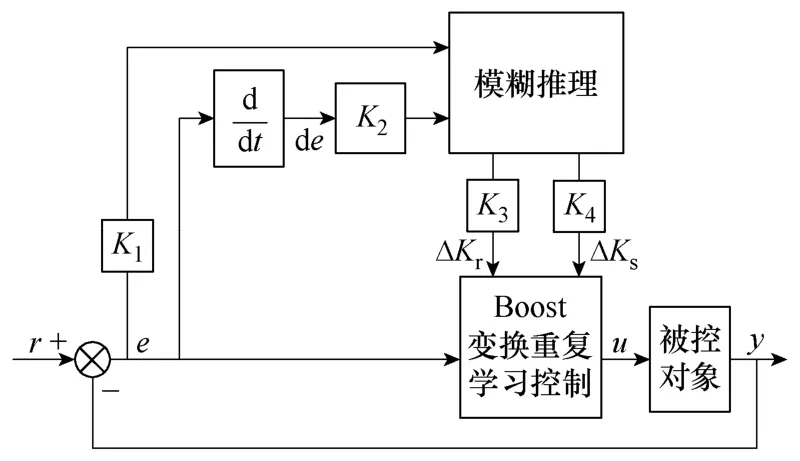
图5 控制器结构框图Fig.5 Block diagram of control system

本文选定模糊控制的语言变量为5个词汇，分别对应负大、负中、零、正中和正大：{NB，NM，Z，PM，PB}。模糊论域采用；四级量化档数，输入量以及输出量均采用上述5个状态，则它们的模糊论域为：{-4，-3，-2，-1，0，1，2，3，4}。选取 e与 de的精确论域分别为（-50，50）与（-5000，5000），由此可得到模糊控制的量化因子K1=4/50，K2=4/5000。而输出量ΔKr的变化范围为（-2，2），因此 K3=2/4，ΔKs的变化范围为（-1，1），因此K4=1/4。输入变量e和de采用如图6a所示的三角形和梯形隶属度函数模糊化，输出变量ΔKr和ΔKs采用如图6b所示的三角形隶属度函数模糊化。由于APF在控制中不可能完全做到无差控制，因此在一定的误差范围内，应保持控制器的输出不变，在输入量的模糊化时，将这一区域用梯形隶属度函数模糊化。而反模糊化采用重心法（Centroid）以取得一个较为平滑的输出曲线。

图6 隶属度函数Fig.6 Membership Functions

在重复学习控制策略中，学习因子Ks，也可称为可调增益，主要用于被控对象的幅值补偿，以改善系统的补偿效果以及保证系统稳定性。

在稳定情况且输入为周期信号时，重复环可对输入的误差信号逐周期累加，从而迅速实现下一周期的合理控制。但考虑到其控制量需延迟一周才能体现，故对于系统第一周期或发生突变等不稳定状态时，重复控制作用有限。此时反馈比例控制系数Kr就可以快速跟踪非周期信号，以增强系统动态性能。

文献[9]对参数Ks，Kr的稳定范围及性能影响做了详细地分析。其变化规律如下：Kr越大，系统的响应速度越快，系统的调节精度越高。但其过大易产生超调，甚至会导致系统不稳定。Kr取值过小，则会降低调节精度，使响应速度缓慢。因此，当偏差e的绝对值较大时，为了使系统具有较好的动态响应性能，Kr应取较大的值；当e的绝对值较小时，为了防止超调过大而产生振荡，应减小Kr。

重复控制系数 Ks的作用是消除系统的稳态误差。Ks越大，系统静态误差消除越快，但Ks过大，在响应过程初期由于重复控制的响应滞后性易使系统不稳定，甚至引起振荡；但是Ks过小，将使系统静态误差难以消除，影响系统调节精度。在常规控制中，常将积分环节分离出来，当误差减小至一定范围时，才加入积分环节。因此，当误差的绝对值较大时，为避免系统响应出现较大超调，应限制重复控制的作用，将其从控制器中分离，取Ks为零；随着误差的绝对值较的减小，增大Ks以消除系统稳态误差，提高控制精度。

设参数 Kr、Ks计算式为式（3），则ΔKr和ΔKs的控制规则表见表1和表2所示。

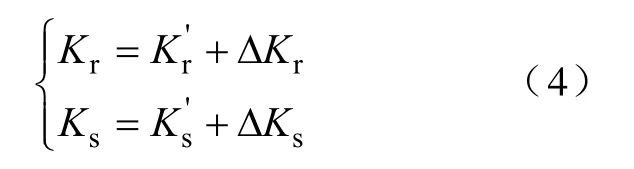
表1 ΔKr的模糊规则表Tab.1 Fuzzy rule table of ΔKr

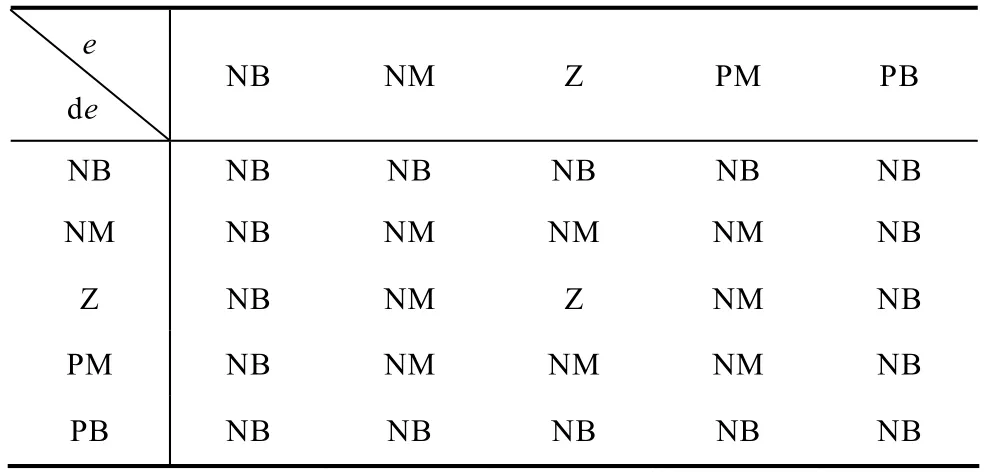
表2 ΔKs的模糊规则表Tab.2 Fuzzy rule table of ΔKs

图7所示为本文所设计的模糊控制器在Matlab中的图形表示。

4 仿真试验

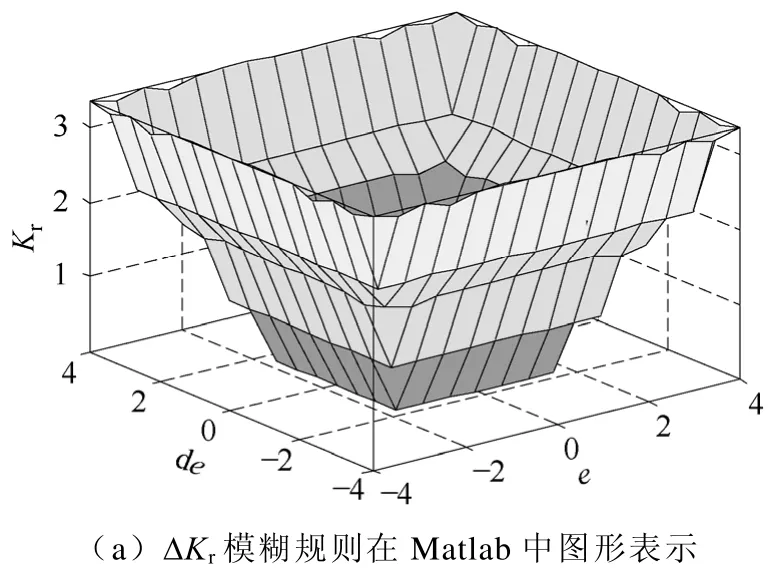
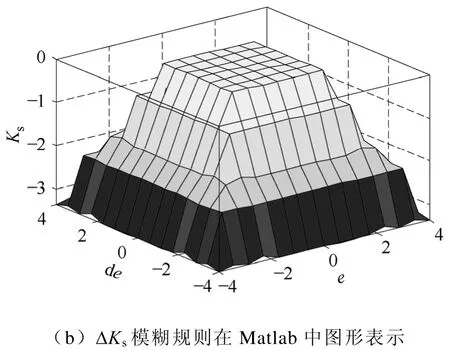
图7 ΔKr和ΔKs在 Matlab 中表示Fig.7 The graphical representation of fuzzy rules ΔKs and ΔKr in Matlab

为表明本文所提出的复合控制策略的可行性，本文对三相并联型有源电力滤波器进行了仿真试验，主要研究该控制策略应用于APF的补偿效果和动态性能。仿真系统中负载为带阻感的三相桥式不控整流器，控制策略为模糊—重复学习复合控制结构。图8a所示为模糊控制器，图8b所示为重复学习控制部分。其中，Ih为谐波误差，K1和K2为输入误差e及误差变化率de的量化因子，K3和K4为输出比例因子。ΔKr和ΔKs为模糊控制器的输出，将其与 Kr和 Ks的初始值相加，即得重复学习控制的真正参数。

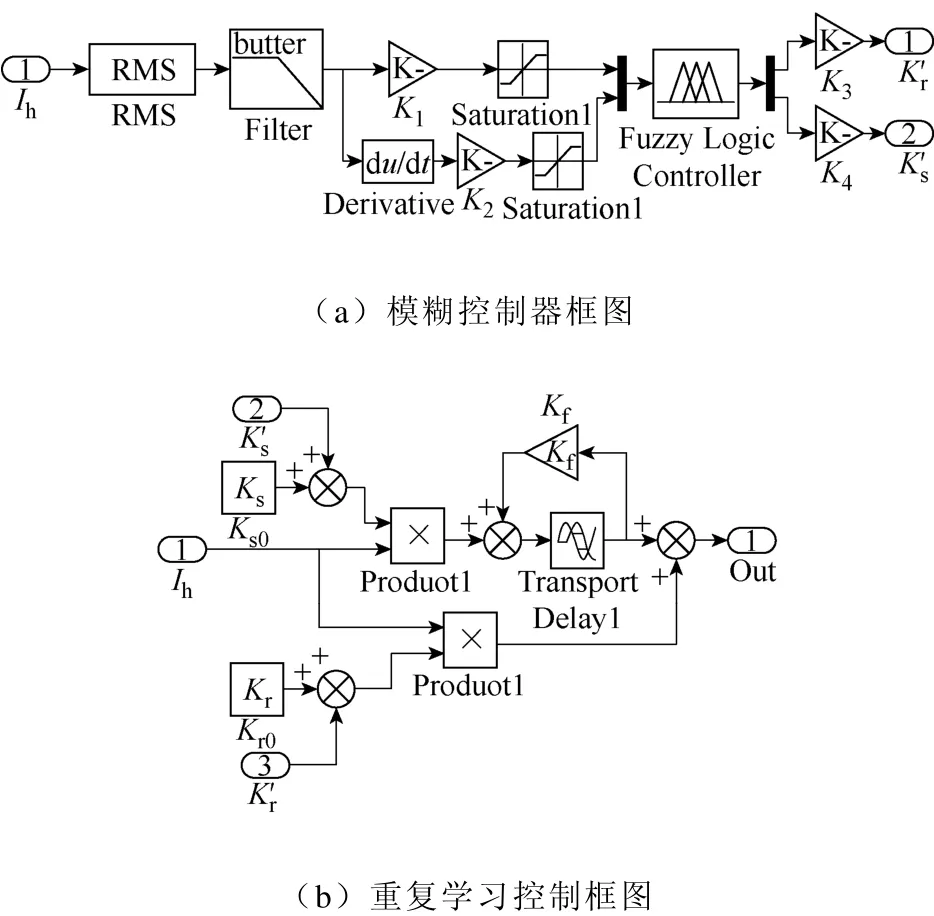
图8 控制框图Fig.8 Conerol diagram

图9为补偿前负载电流波形及FFT分析图。图中电流单位均为安培，与图10所示类似。由图可知此时负载电流基波为 466.2A，谐波总畸变率 THD为 23.33%。投入采用复合控制的 APF补偿后，系统电流波形如图10所示，电流波形已明显改善，谐波总畸变率也大大降低，仅为3.74%。

图9 补偿前负载电流及其FFT分析Fig.9 FFT analysis and the load current before compensation

图10 补偿后系统电流及其FFT分析Fig.10 FFT analysis and the system current after compensation

为了更加清楚地观察加入模糊控制对补偿效果的改进，本文分别对负载发生突变时采用复合控制策略及传统重复学习控制策略两种 APF系统做仿真对比。图11a所示为负载在t=0.2s时发生突变的电流波形。从0.2s开始计算负载电流的谐波总畸变率，如图11b所示，为22.22%。

采用复合控制策略的APF补偿后，系统电流波形及THD变化如图12所示，在负载电流突变后，THD的峰值为7.5%，且在t=0.25s时，系统电流的THD降为 3.5%，之后重复控制量逐渐增大来消除稳态误差。

图11 负载突变后的电流及其谐波Fig.11 Load current and its harmonics after load sudden change

图13a所示为传统的重复学习控制APF补偿后的系统电流波形。在图13b所示中，负载电流突变后，系统电流 THD的峰值为 7.8%，且在t=0.25s时，系统电流的THD为4.5%，相对于采用复合控制的 APF，显然其跟踪速度较慢，动态响应性能较差。

图12 复合控制系统电流及其THDFig.12 System current and its THD under the composite control

图13 传统重复学习控制下的系统电流及其FFTFig.13 System current and its FFT analysis under the traditional repetitive learning control

5 结论

本文针对并联型有源电力滤波器提出了一种模糊—重复学习复合控制策略。该方式在保证系统稳定性的前提下，综合提高了系统的动态响应速度及稳态误差精度，有效地改善了有源电力滤波器的谐波补偿效果。仿真结果也表明了这种控制策略的有效性和优越性。

[1]查晓明, 孙建军, 陈允平. 并联型有源电力滤波器的重复学习Boost变换控制策略[J]. 电工技术学报,2005, 20(2): 56-62.Zha Xiaoming, Sun Jianjun, Chen Yunping. Boost transform repetitive learning control strategy in parallel active power filter[J]. Transactions of China Electrotechnical Society, 2005, 20(2): 56-62.

[2]武健, 徐殿国, 何娜. 并联有源滤波器输出 LCL滤波器研究[J]. 电力自动化设备, 2007, 27(1): 17-20.Wu Jian, Xu Dianguo, He Na. The output LCL filter of Shunt active filter [J]. Electric Power Automation Equipment, 2007, 27 (1): 17-20.

[3]刘飞, 殷进军, 周彦, 等. LCL滤波器的三相光伏逆变器双环控制策略[J]. 电力电子技术, 2008, 42(9)： 29-31.Liu Fei, Yin Jinjun, Zhou Yan, et al. The double loop control strategy of three-phase PV inverter with LCL filter [J]. Power Electronics, 2008, 42(9): 29-31.

[4]付青, 罗安, 王莉娜. 基于自适应智能控制的混合有源电力滤波器复合控制[J]. 电机工程学报, 2005,25(14): 46-51.Fu Qing, Luo An, Wang Lina.A Composite control of hybrid active power filter with adaptive intelligent control[J]. Electrical Engineering, 2005, 25(14):46-51.

[5]李剑, 康勇, 陈坚. 带模糊调节的重复控制器在逆变器中的应用[J]. 电气传动, 2001, 36(6): 30-34.Li Jian, Kang Yong, Chen Jian. A repetitive controller of the inverter with fuzzy tuning[J]. Electrical Transmission, 2001, 36(6): 30-34.

[6]李刚, 罗安, 付青, 等.一种新型混合型有源滤波器的模糊PI控制[J]. 电力电子技术, 2005, 39(4)： 91-93.Li Gang, Luo An, Fu Qing, et al. A new type of hybrid fuzzy PI control of active power filter [J].Power Electronics Technology, 2005, 39 (4): 91-93.

[7]Harold L Broberg, Richard G Molyet. A new approach to phase cancellation in repetitive control[C].Proceedings of the IEEE Industry Applications society Annual Meeting 1994: 1766-1770.

[8]Wang Y N. An adaptive control using fuzzy logic neural network and its application. 1995, 12(4):437-444.

[9]杨柳. 重复学习控制器设计及结合模糊控制理论的性能改进[D]. 武汉大学出版社.

[10]鲁东海. 并联型有源电力滤波器迭代学习控制的应用研究[C]. 武汉: 武汉大学出版社.

[11]夏文启. 并联型有源电力滤波器的LCL滤波和延时性研究[D]. 武汉: 武汉大学出版社.

[12]钱挺, 吕征宇, 胡进, 等.单周控制的有源电力滤波器双环控制策略[J]. 电机与控制学报, 2003, 23(3)： 34-37.Qian Ting, Lv Zhengyu, Hu Jin, et al. A double loop control strategy for active power filter with one-cycle control[J]. Electric Machines and Control, 2003,23(3): 34-37.

[13]于少娟, 齐向东, 吴聚华.迭代学习控制理论及应用[M].北京: 机械工业出版社, 2005.

[14]窦振中.模糊逻辑控制技术及其应用[M].北京:北京航空航天大学出版社,1995.