粒子群优化模糊PI算法的永磁同步电机控制
2011-07-02付光杰郑连亮
付光杰,张 雷,郑连亮
(1.东北石油大学 电气信息工程学院,黑龙江 大庆 163318;2.辽河石油装配制造总公司,辽宁 盘锦 124010)
1 引言
永磁同步电机(PMSM)具有较高的能量密度和效率,其体积小、惯性低、动态响应快,非常适应于拖动系统的执行,有极好的应用前景。因此,在可逆轧机、矿井卷扬机等这样一些要求非常高的拖动系统中电动机都选用PMSM作为驱动部件。传统的电动机采用的控制策略通常是PID控制,因为这种方法简单成熟,实用化程度较高,但是PID控制器本身具有一定的局限性,即控制参数不能随环境变化而调整,不具有整体优化功能[1]。许多学者开始采用一些智能控制策略如神经网络控制或模糊控制,但这些方面都有各自的缺陷,如神经网络控制复杂、困难、鲁棒性差;而单纯的模糊控制对模糊规则选择以及比例参数变化敏感[2]。针对这一情况,本文提出一种粒子群优化自适应PI模糊控制器(PFC),即利用粒子群算法优化模糊控制器的2个参数因子kp、ki,这样就可以随环境变化以及负载变化实时跟踪模糊控制器的参数变化,使得模糊控制器的鲁棒性和控制精度都能提高。
2 永磁同步电机的数学模型
根据2极贴面式永磁同步电动机的空间矢量关系,得电压方程为:
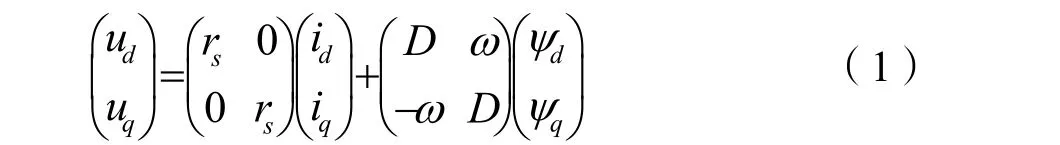
磁链方程为:
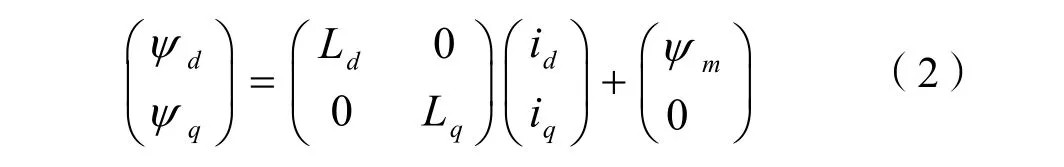
转矩方程为:

式中:D=d/dt为微分算子;rs为定子三相绕组电阻;Ld、Lq分别为d轴和q轴绕组电感;Ud、Uq分别为d轴和q轴绕组电压;ω为转子角速度;Id、Iq分别为d轴和q轴绕组电流;mψ为永磁体磁通。
3 模糊自适应PI算法
运用模糊数学的基本理论和方法,把规则的条件、操作等用模糊集表示,并把这些模糊控制规则及有关信息(如评价指标、初始PI参数等)作为知识存入计算机知识库中,然后计算机根据控制系统的实际响应情况,运用模糊推理,即可实现对PI参数的最佳调整,这就是模糊自适应PI控制(FuzzyPI)。
模糊自适应PI控制器以误差e和误差变化率e˙作为输入,可以满足不同时刻的e和e˙对PI参数自整定的要求。利用模糊控制规则对PI参数进行在线调整修改从而使被控对象有良好的动静态性能[3],其结构如图1所示。
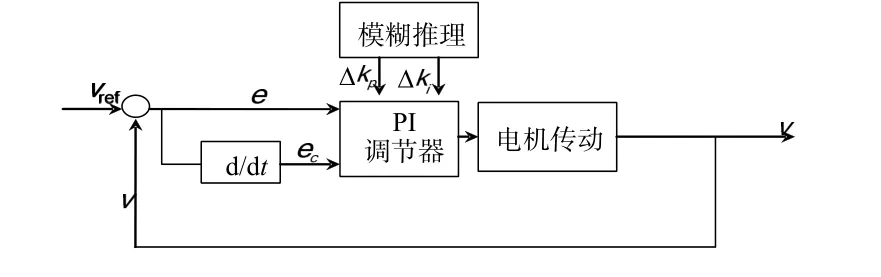
图1 基于自适应PI模糊控制器的电机控制
4 粒子群优化算法

粒子在找到上述2个极值后,就根据下面2个公式来更新自己的速度与位置:
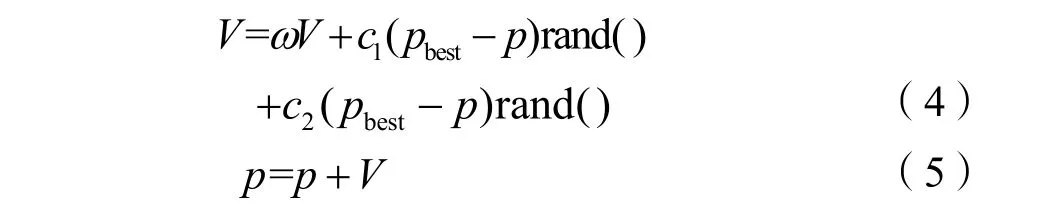
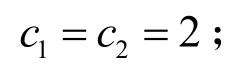
粒子通过不断学习更新,最终飞至解空间中最优解所在的位置,搜索过程结束,最后输出的gbest就是全局最优解。在更新过程中,粒子每一维的最大速率被限制为Vmax,粒子每一维的坐标也被限制在允许范围之内[5]。
粒子群优化算法没有交叉与变异运算,所以算法结构简单,运行速度快。但是,基本粒子群优化算法在解空间内搜索时,有时会出现粒子在全局最优解附近“振荡”的现象,为了避免这个问题,可以作如下改进:
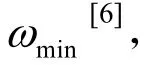

其中:k为当前叠代数;kmax为总的迭代次数。
5 基于粒子群优化的自适应PI模糊控制器
图2给出了典型的基于自适应PI模糊控制器的电机控制结构,它不依赖于电机的具体参数,当选用合适的模糊控制表后系统具有较强的鲁棒性。但是一张模糊控制表很难同时满足各种工况的要求,这就要求模糊控制规则或参数在运行过程中可以自动地调整、修改和完善。为此本文根据系统反馈信息粒子群优化技术动态调节比例因子kp和积分因子ki,以获得最佳控制效果。
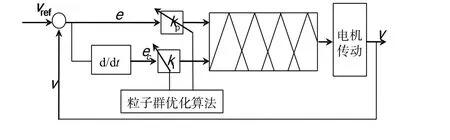
图2 基于粒子群优化的自适应PI模糊控制器结构
粒子群优化的自适应PI模糊控制器在电机运行暂态过程中,PSO及时更新优化模糊控制的2个参数,而且程序简单,语句少,运行时间短,具体步骤如下:
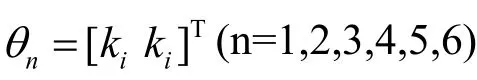
在第t次迭代时,粒子i的飞行速度和位置分别表示为:
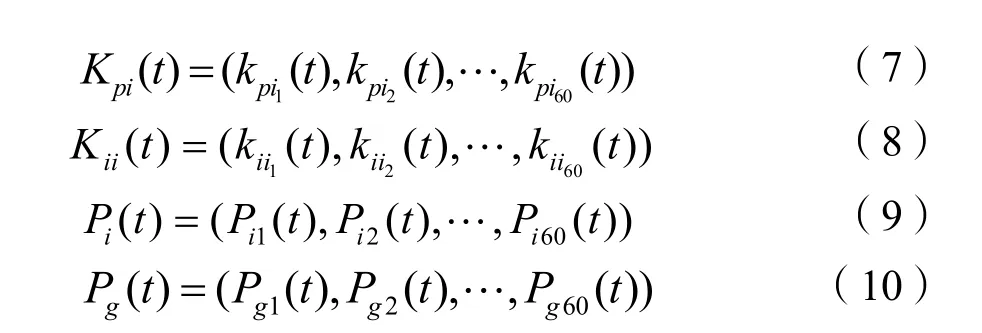
在第t+1次迭代计算时,粒子i根据下列规则来更新自己的速度和位置:

(2)将第t次的值代入式(11)、(12)中得到第t+1次的位置和速度,按式(14)检验适应度函数JITAE。然后找到新的个体极值并与全局极值比较,若新的个体极值比上一次的全局极值更优,则替换为新的全局极值。
(3)以此类推,粒子在空间不断变异寻找最优解,直到该粒子满足目标函数 JITAE≤ 0 .0001,程序中止,此时粒子所在的位置就是模糊控制器2个参数比例因子kp和积分因子ki的最优值。否则,程序回到(2),继续寻找。
6 仿真实验
本仿真中永磁同步电机的参数为额定功率1kW,额定电压为 380V,额定转速为 1000r/min,调速范围为200~1500r/min,图3为基于自适应PI模糊控制器的仿真模型框图,通过模糊逻辑控制单元对Δkp和Δki进行模糊化和解模糊化进而调整ki和kp。
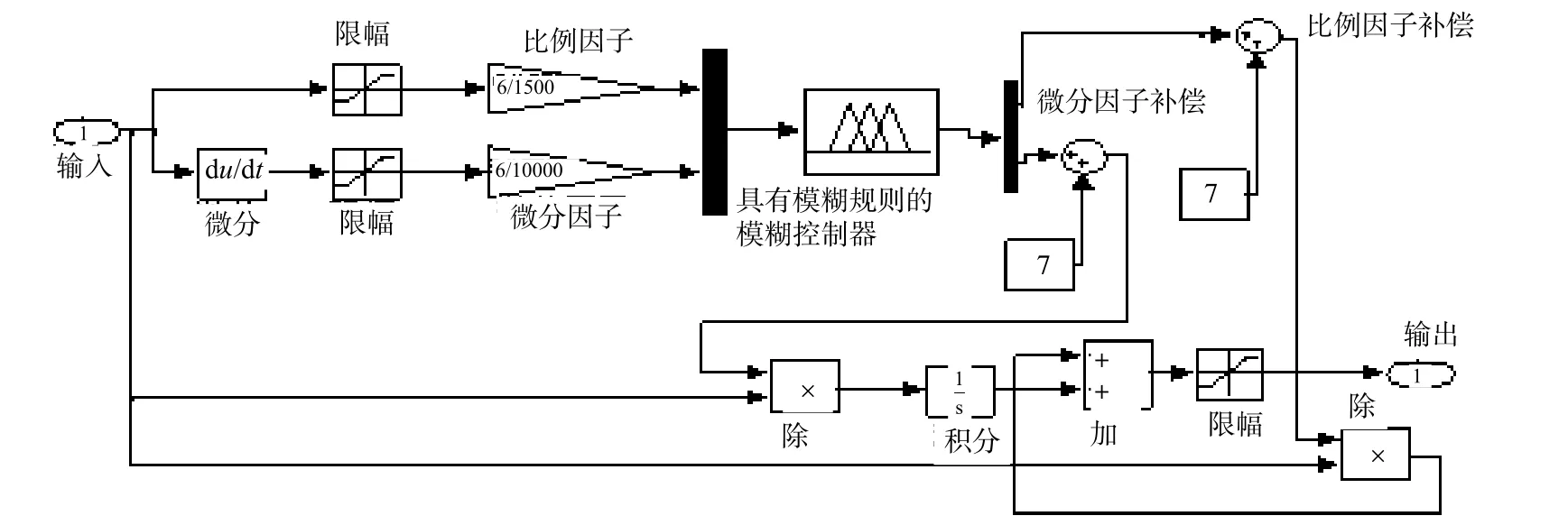
图3 自适应PI模糊控制器的仿真模型
图4为基于粒子群优化PI模糊闭环矢量控制仿真框图。在外环即速度环中,速度指令为200~1500r/min和反馈产生的速度误差e送到PSO中优化模糊控制器的2个参数kp、ki,输出u作为电流指令,进入到电流环,PWM的产生方式为空间电压矢量脉宽调制(SVPWM),输出三相正弦电流驱动电机,其输出波形如图5~10所示。
在仿真过程中,分别对自适应 PI模糊控制器和PFC控制器作用的系统进行仿真,在转速设定为1000r/min和200r/min时,两种控制器作用下的转速响应曲线如图5和图6所示。曲线2为PFC控制器作用下的速度响应曲线,曲线1为自适应PI模糊控制器作用下的速度响应曲线,可以看出,无论是在响应速度上,还是超调量大小方面,2曲线都要优于1。
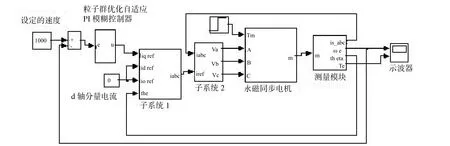
图4 基于粒子群优化PI模糊闭环矢量控制仿真

图5 1000r/min时转速响应曲线

图6 200r/min时转速响应曲线
为了测试在应用PSO优化后控制系统的抗干扰能力,将转速设为1100r/min,转矩从初值1N⋅m跃变到16N⋅m时转矩变化情况如图7和8所示,图7为PFC作用下的转矩响应曲线,图8为自适应模糊PI作用下的转矩响应曲线。由此可见,PFC作用下的响应曲线振荡较小且超调量较小,调整时间只有 0.1s,鲁棒性较好,而自适应模糊PI作用下的响应曲线振荡较大且超调量较大,调整时间却有 0.2s,鲁棒性较差。当转速设为 1100r/min,负载由14N⋅m突变为 16N⋅m 时,转速的变化情况如图9和10所示。图9为PFC作用下的转速响应曲线,图10为自适应模糊PI作用下的转速响应曲线,图9中的转速变化较平缓,而图10中的转速波动较大。
7 结论
针对传统的永磁同步电机控制采用模糊 PI(Fuzzy PI)控制策略而引起的参数容易改变,不稳定的特点,本文提出了一种新的控制策略,即利用粒子群算法对PI模糊控制器的2个参数因子kp、ki进行全局优化,充分发挥了粒子群算法的快速性,并利用Matlab工具进行了仿真。结果表明,该方法具有很强的鲁棒性和动态性能,能满足拖动系统中负载变化快的要求。
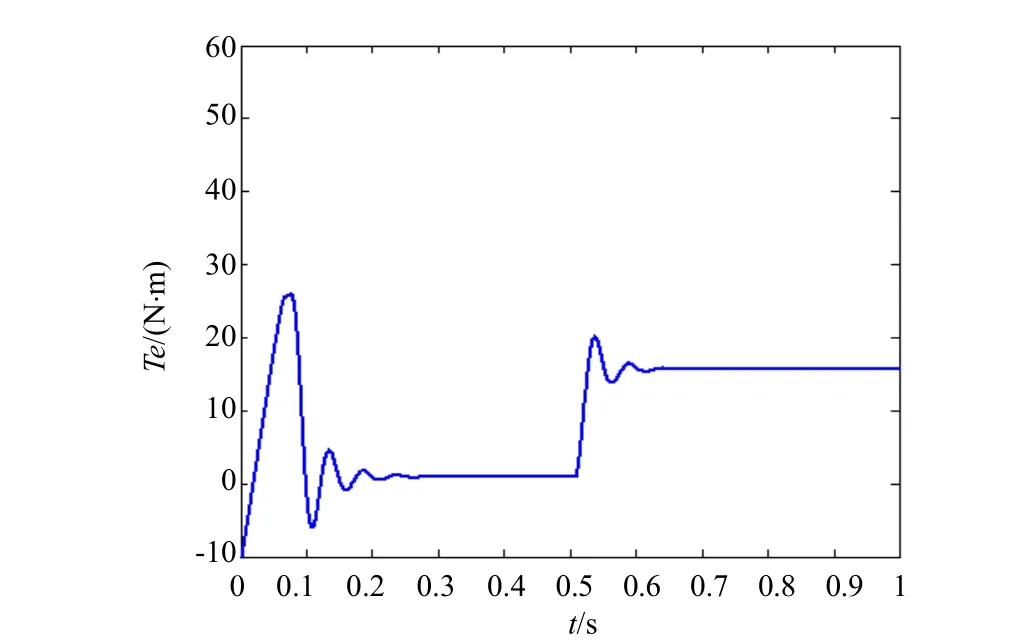
图7 1100r/min时PFC作用下转矩响应曲线

图8 1100r/min时Fuzzy PI作用下转矩响应曲线
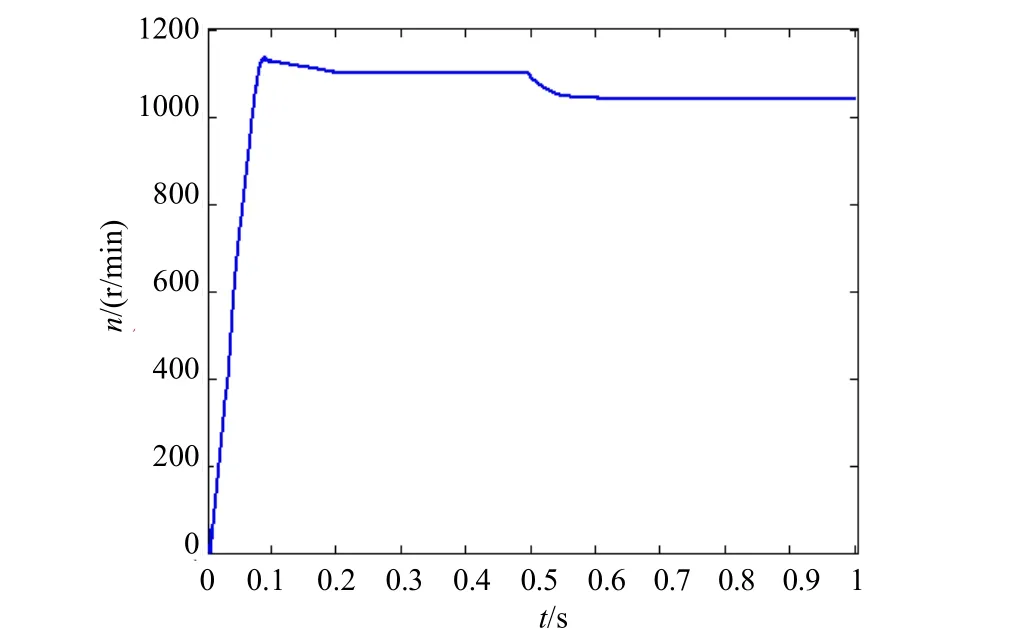
图9 负载突变时PFC作用下转速响应曲线
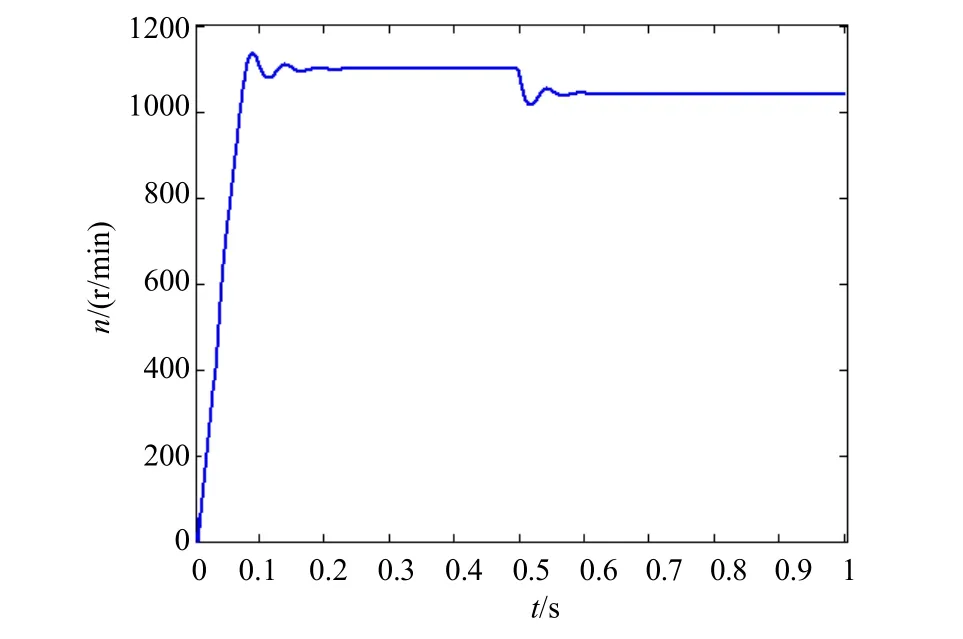
图10 负载突变时Fuzzy PI作用下转速响应曲线
[1]王洋, 刘永光. 基于 Simulink的永磁同步电机矢量控制系统仿真[J]. 组合机床与自动化加工技术,2011(2): 78-82.
[2]雷霞, 周广文. 改进的加热过程模糊自调整 PID算法及仿真分析[J]. 吉林大学学报(信息科学版),2008(5): 547-552.
[3]郑敏, 杨成忠. Fuzzy-PID多模态控制器在永磁同步电机中的应用[J]. 机电工程, 2009(4): 44-46.
[4]包广清, 刘家兵. 基于粒子群优化模糊控制器无刷直流电机控制[J]. 电气自动化, 2009(2): 30-32.
[5]安凤栓, 常俊林, 苏丕朝, 等. 基于改进粒子群优化算法的 PID控制器参数优化[J]. 工矿自动化,2010(5): 54-57.
[6]刘微, 陈贺新, 陈瀚宁, 等. 改进的 PSO 算法在RFID网络调度中的应用[J]. 吉林大学学报(信息科学版), 2011(2): 121-127.
