水轮发电机定子铁心等效工程弹性常数计算及屈曲分析
2011-07-02徐忠海赫晓东王荣国
徐忠海, 赫晓东, 王荣国
(1. 哈尔滨工业大学材料科学与工程博士后流动站,哈尔滨 150080;2. 哈尔滨工业大学特种环境复合材料技术国防科技重点实验室,哈尔滨 150080)
1 引言
随着水轮发电机单机容量的不断增大,发电机电磁负荷也相应提高,定子铁心和机座的振动[1-9]及热变形产生的定子翘曲[10]也上升到一个显著的地位。国内外研究水轮发电机定子和机座的刚度、强度、振动以及定子翘曲的分析计算中遇到一些不确定参数,它们对计算分析结果有着较大的影响,但至今国内外还没有统一的数据可参考,这就是定子铁心的等效弹性常数。

本文将铁心叠片和通风槽钢分别看做两种不同的叠层,利用厚层合板模型计算定子铁心的等效工程弹性常数,并利用计算得到的铁心叠片弹性常数对其进行屈曲模拟分析。
2 等效工程弹性常数的三维计算模型
考虑一个由许多同一子层组重复铺叠而成的厚复合材料层合板[17],并假设这个子层组的厚度和整个层合板的厚度比起来是非常小的,这样将该层合板等效为一个三维的、均匀的、各向异性的实体。取这个子层组作为这一实体的代表性体积单元,它是由N层具有正交各向异性的单向纤维复合材料薄层按任意方向铺叠而成。令x轴和y轴位于子层组的平面内,z轴垂直于该平面,如图1所示建立直角坐标系。

图1 代表性体积单元
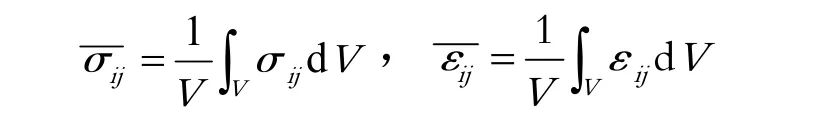
上式中V是单元的体积,σij和εij分别为单元内任一点处的应力和应变。令单元各层上的应力和应变均为常数,则由上面两式可得

为了满足单元内层与层之间界面处应力的连续性,假设各层上z方向的正应力以及与z方向相应的层间剪应力均是相等的,则有
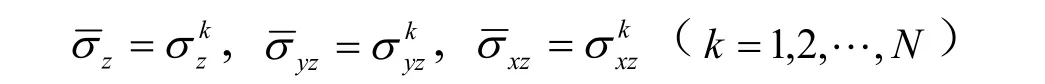
为了满足位移的连续性,假设各层的x、y方向上的正应变以及xy平面内的剪应变均是相等的,则有

由于单元中各单层的铺叠方向是任意的,则它的应力-应变关系可表达为

通过联立上述方程并经过计算推导,得到单元等效应力-应变关系为:
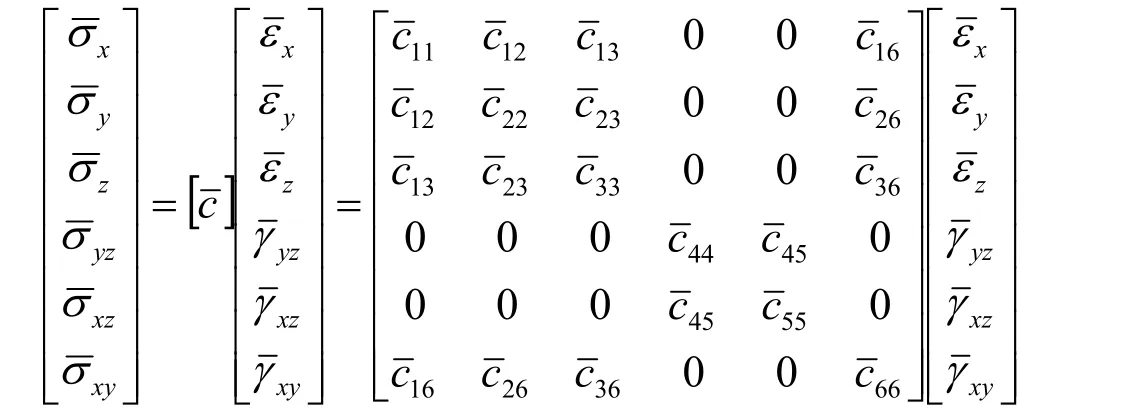
其中各等效弹性常数为:

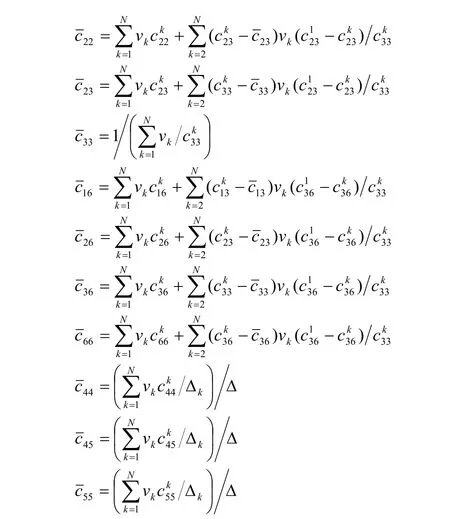
上式中

则单元的等效弹性柔度矩阵为:

最后,得到单元的等效工程弹性常数为:

3 定子铁心等效工程弹性常数的计算
定子铁心是由铁心叠片和通风槽钢两部分交错压叠而成,将铁心叠片和通风槽钢看作两种不同的叠层,进而将它们放在一起看作一个子层组,这样定子铁心就可看作是由很多这样的子层组重复铺叠而成的复合材料层合板。虽然整个定子铁心是由铁心叠片和通风槽钢堆叠而成,但这里我们将其做实体分析;同时认为拉紧螺杆能提供足够大的预紧力,使得整个定子铁心在预紧力的作用下“黏结”牢固,没有相对滑移。因此,定子铁心的等效工程弹性常数可以用上面的厚层合板模型来计算。值得注意的是,这样得到的结果是安装状态下的情况,没考虑温度、电磁场等对定子铁心的影响。
对定子铁心的结构分析可知,它可整体的视为是一种横观各向同性材料,即在xy平面内是各向同性的,而z方向具有与之不同的弹性性能。通过 Matlab编程计算得到某电机厂研制生产的某型号水轮发电机定子铁心的等效工程弹性常数与实际的分析情况是相符的,并且在xy平面内Ex、νxy和Gxy满足关系式
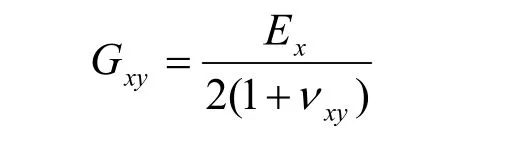
4 叠片屈曲分析
我们把针对某电机厂研制生产的某型号水轮发电机定子铁心计算得到的铁心叠片等效工程弹性常数作为输入参数来研究单片叠片的屈曲问题。由于一段叠片中,与通风槽钢最近的一张叠片最容易先屈曲,所以选取一张与通风槽钢焊接在一起的单片叠片进行屈曲分析。引起叠片屈曲的因素有两个,一个是温度,另一个是磁拉力,这里只对温度引起的屈曲进行研究。
叠片与定位筋连接处施加径向约束,周期对称边界处施加环向约束,通风槽钢的一端施加轴向约束,为整个叠片和通风槽钢施加 8度的温升。首先进行静态力学分析,求出单片叠片在 8度温升下的应力和变形,然后进行屈曲分析,求出前4阶屈曲临界载荷系数。
忽略机座刚度时,单片叠片在8度温升下最大应力为 52.323MPa,在该条件下计算得到的前4阶屈曲临界载荷系数见表1所示。
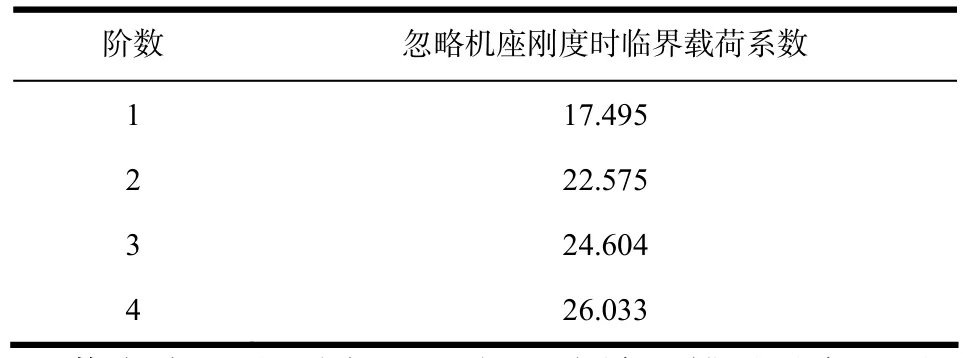
表1 屈曲临界载荷系数
若考虑机座刚度,即在叠片鸽尾槽处施加机座的弹簧刚度,则单片叠片在 8度温升下最大应力为33.539MPa,此时计算得到的前4阶屈曲临界载荷系数见表2所示。
我们如果利用从阿尔斯通公司引进的屈曲理论计算公式来计算该单片叠片的一阶屈曲临界载荷系数,那么得到的结果为28.08,而前面采用有限元方法并考虑定子机座的刚度后计算得到的一阶屈曲临界载荷系数为23.86,二者间有一定的差别。这是由于理论算法是把机座与铁心简化为两个有过盈配合的套筒计算的,计算一阶屈曲临界载荷系数时又把铁心叠片的弹性基础刚度考虑在内。而叠压弹性基础刚度的取值是决定一阶屈曲临界载荷的主要因素,该值一直沿用阿尔斯通公司的实验数据;而有限元方法计算的屈曲临界载荷系数主要取决于机座的刚度,机座的刚度可根据机组结构的不同计算出来,因此结果更接近于实际情况。

表2 屈曲临界载荷系数
5 结论
水轮发电机定子铁心的等效弹性常数是电机工业力学分析计算中的关键环节之一。本文从理论上研究了水轮发电机定子铁心等效工程弹性常数的计算问题,通过利用计算得到的数据对其进行了屈曲分析,并将模拟结果与理论结果进行了比较,说明了有限元方法模拟结果的可信性。同时该计算程序的完成,使得我们可以在缺乏试验数据的情况下直接计算,为以后机组的投标和中标后的设计生产提供了技术支持,并为今后百万千瓦级水轮发电机的设计提供更精确可靠的数据。
[1]Richardson P, Hawley R. Generator Stator Vibration[C]. IEEE Winter Power Meeting, 1970:53-61.
[2]Garvey S D. The Vibrational Behaviors of Laminated Components in Electrical Machines[C].Proc. International Conference on Electrical Machines and Drives, IEE, London, 1989: 226-231.
[3]Tampion A A, Stoll R L, Syklski J K. Variation of Turbogenerator Stator Core Vibration with Load[C].IEE Proceedings-C Generation Transmission and Distribution, 1991, 138(5): 389-400.
[4]Watamble S, Kenj S, Ide K, Sato F, Yanamoto M.Natural Frequencies and Vibration Behavior of Motor Stators[C]. IEEE Trans, 1996, 102: 949-956.
[5]Garvey S D, Glew C N. Magnetostrictive Excitation of Vibration in Machines---a Modal Approach[C].Ninth International Conference on Electrical Machines and Drives, Conference Publication, 1999,468: 169-173.
[6]Qing G H, Qiu J J, Hu Y D. Vibration Analysis of Large Turbogenerator Stator System[C].International Conference on Power System Technology Proceedings, 2002: 2168-2172.
[7]许实章. 水轮发电机定子铁芯的磁振动[J]. 华中工学院学报, 1973(12): 78-96.
[8]钱学智, 董航新. 用有限元法计算水轮发电机定子铁芯的磁振动[J]. 大电机技术, 1989(4): 1-5.
[9]沈旭东. 次谐波引起的铁芯振动分析[J]. 大电机技术, 1988(1): 20-25.
[10]刘禄臣. 水轮发电机定子的磁振动与热膨胀[J].大电机技术, 1981(4): 12-22.
[11]哈尔滨电工学院. 水轮发电机的振动[J]. 大电机技术, 1974(1).
[12]哈尔滨大电机研究所. 应用电子计算机计算水轮发电机次谐波引起的电磁振动[J]. 大电机技术,1974(1): 23-35.
[13]Richardson P. Stator Vibration in Large Two-Pole Generator[C]. IEEE Winter Power Meeting, 1966:1021-1030.
[14]Walker J H, Member etc. Pressing and Clamping Laminated Cores[C]. Proc. The Institution of Electrical Engineers, Power IEE, 1964, 111(3):565-577.
[15]裘文干, 张云程, 施惠智, 季鲁军. 定子铁心的计算弹性常数[J]. 大电机技术, 1986(1): 41-44.
[16]钱学智, 董毓新, 沙锡林. 水轮发电机定子机座铁心耦联振动分析[J]. 大电机技术, 1991(2):13-19.
[17]Sun C T, Li S. Three-Dimensional Effective Elastic Constants for Thick Laminaties[J]. Journal of Composite Materials, 1988, 22(7): 629-639.
