相位求差法与相位率法探测与修复周跳的比较
2011-06-30雷雨高玉平刘娜
雷雨,高玉平,刘娜
相位求差法与相位率法探测与修复周跳的比较
雷雨1,2,高玉平1,2,刘娜1,2
(1. 中国科学院国家授时中心, 西安 710600;2. 中国科学院时间频率基准重点实验室, 西安 710600)
目前对GPS载波相位观测值周跳的探测与修复有多种方法,但是各种方法都不很完善。介绍常用的周跳探测与修复方法,并利用相位求差法和相位率法进行周跳探测与修复试验。结果表明2种方法均能准确地锁定发生小周跳的历元,而且能高效地修复观测值;然而,相位求差法需要双频观测数据,而相位率法仅需要单频观测数据。
周跳探测与修复;载波相位;相位求差;相位率
载波相位测量是GPS导航定位等应用中广泛采用的方法[1]。如果在跟踪卫星过程中,由于某种原因(如卫星信号被障碍物挡住而暂时中断,或受无线电信号干扰而造成失锁)导致计数器无法连续计数,那么,当信号重新被跟踪后,整周计数就不正确(但是不到一个整周的相位观测值仍是正确的),这种现象称为周跳(cycle slip)[2]。周跳是GPS载波相位观测值中特有的问题,它是提高导航定位精度的一个限制性因素。研究表明,未被探测的周跳将主要被整周模糊度参数、接收机位置等参数所吸收,从而导致对这些参数的有偏估计[3]。因此,周跳的探测与修复是GPS数据预处理阶段最为重要的任务之一。
目前,周跳的探测与修复方法有多种,如高次差法、Blewitt方法、伪距/相位组合法、电离层残差法等[4-6],但是各种方法都不很完善,尤其对于小周跳还不能有效地探测和修复。高次差法只适用于大周跳的探测且不能探测连续周跳;伪距/相位组合法探测周跳的能力取决于伪距观测量的精度、组合波长的长度及数据采样率,该法精度较低;电离层残差法可以探测与修复周跳,但其推证方法不够完善,同时由于没有解决周跳解的多值性问题,因此,该法只能修复小于5周的周跳;Blewitt方法是目前使用较多的周跳探测方法,但其计算过程复杂且具有一定的局限性[7]。下面对相位求差和相位率周跳探测与修复方法进行分析比较。
1 双频载波相位求差法
1.1 双频载波相位求差法探测与修复周跳原理
目前GPS卫星以L1和L2两个波段(其频率分别为1.57542GHz、1.2276GHz)发射载波信号。假设由测站观测得到的来自卫星的载波信号的相位观测值为,则测相伪距观测方程可写为
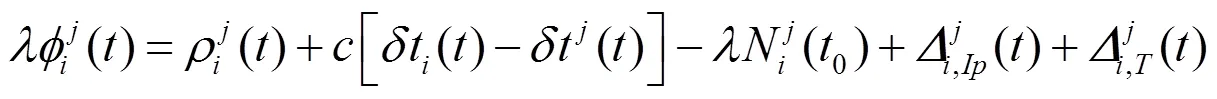

(2)

令

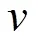
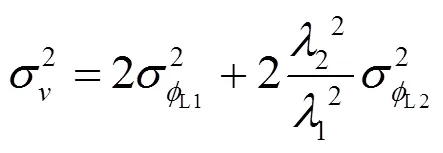

或
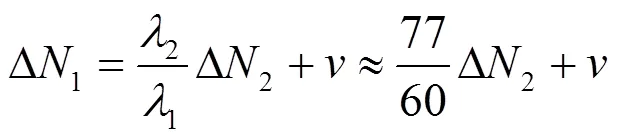
1.2 利用伪距差分约束确定周跳值



比较式(2)和式(9)可得

由此可得

2 相位率法
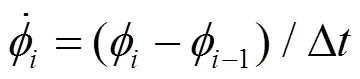


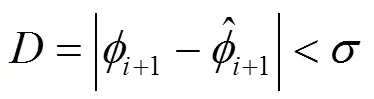
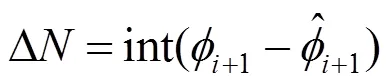
3 算例比较
3.1 数据准备与预处理
从ftp://igscb.jpl.nasa.gov/下载了某IGS跟踪站的观测数据进行试验,接收机采样率为1 s,观测值类型包括L1,L2,P1,P2,C1,S1和S2[12]。事先用Bernese软件对某日04:00:00到04:59:59(GPS时间,简称GPST)期间共3 600个历元的观测数据进行周跳探测,探测结果表明观测值中无周跳。
为了验证相位求差法和相位率法在各种情况下探测与修复周跳的能力,需要考虑周全的测试情况。首先,当单一频率载波发生小周跳或大周跳时的探测和修复;其次,当2种载波在相同历元发生同样大小周跳时的探测和修复;最后,当2种载波在相同历元发生大小不等周跳时的探测和修复。
按照上述验证思路,选取PRN为03的卫星作为计算星,在相位观测值中人为加入周跳,测试在各种情况下,2种方法探测周跳的能力。具体加入的周跳见表1。
表1 模拟周跳
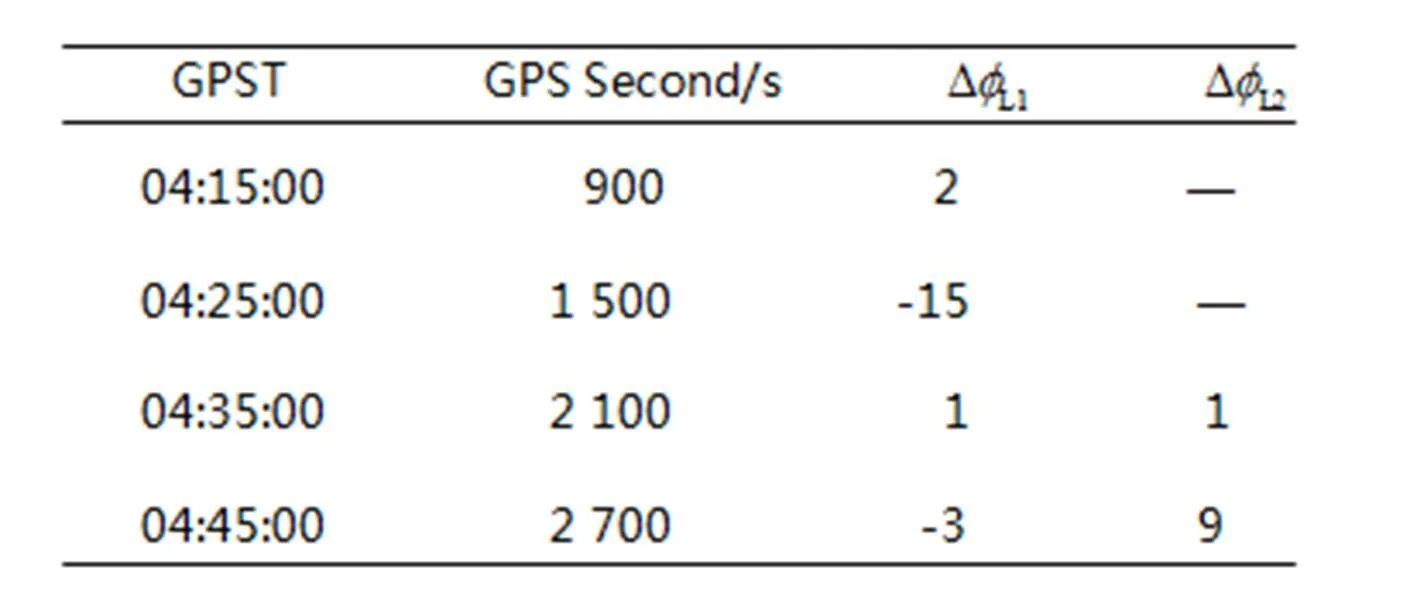
3.2 试验分析
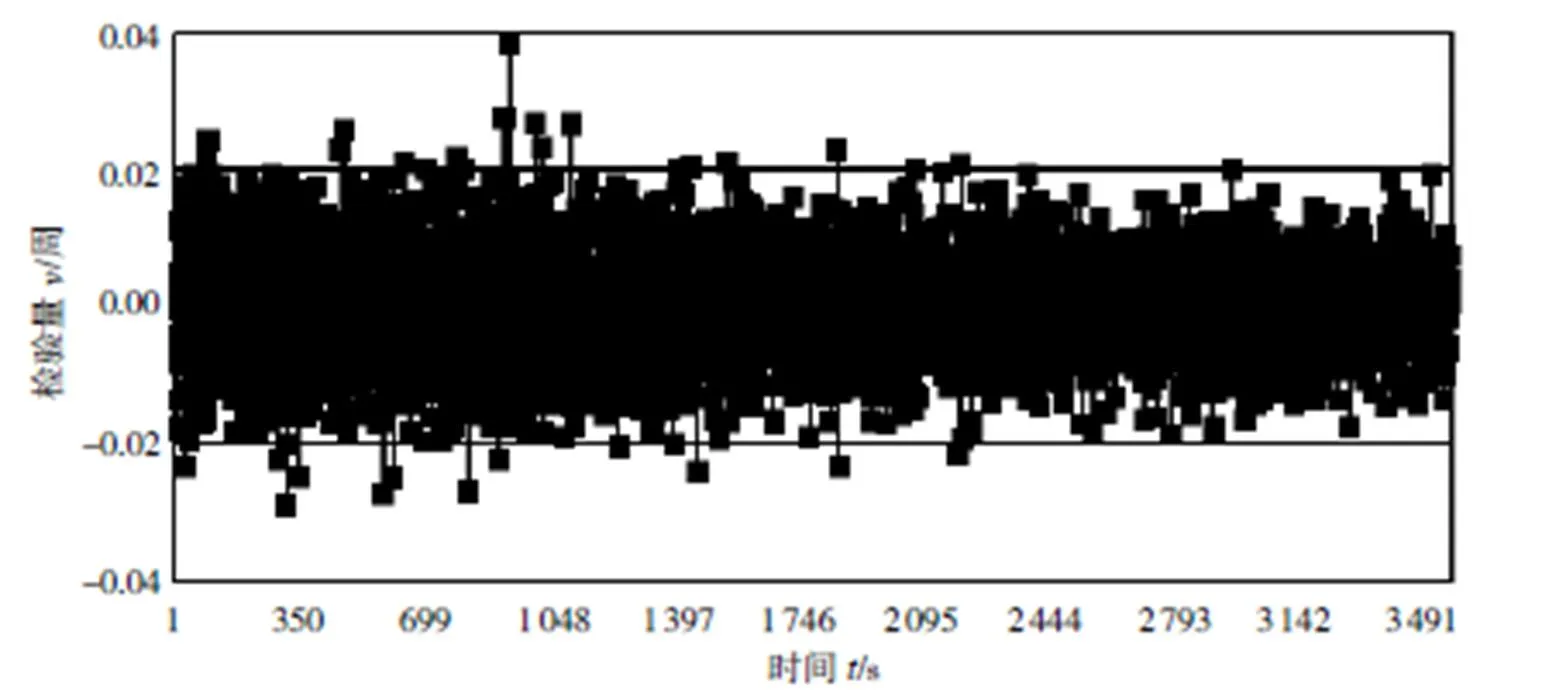
图1 相位求差法得到的检验量v 时间序列(无周跳)

图2 相位求差法得到的检验量v 时间序列(有周跳)

图3 L1载波相位率法得到的检验量D(无周跳)
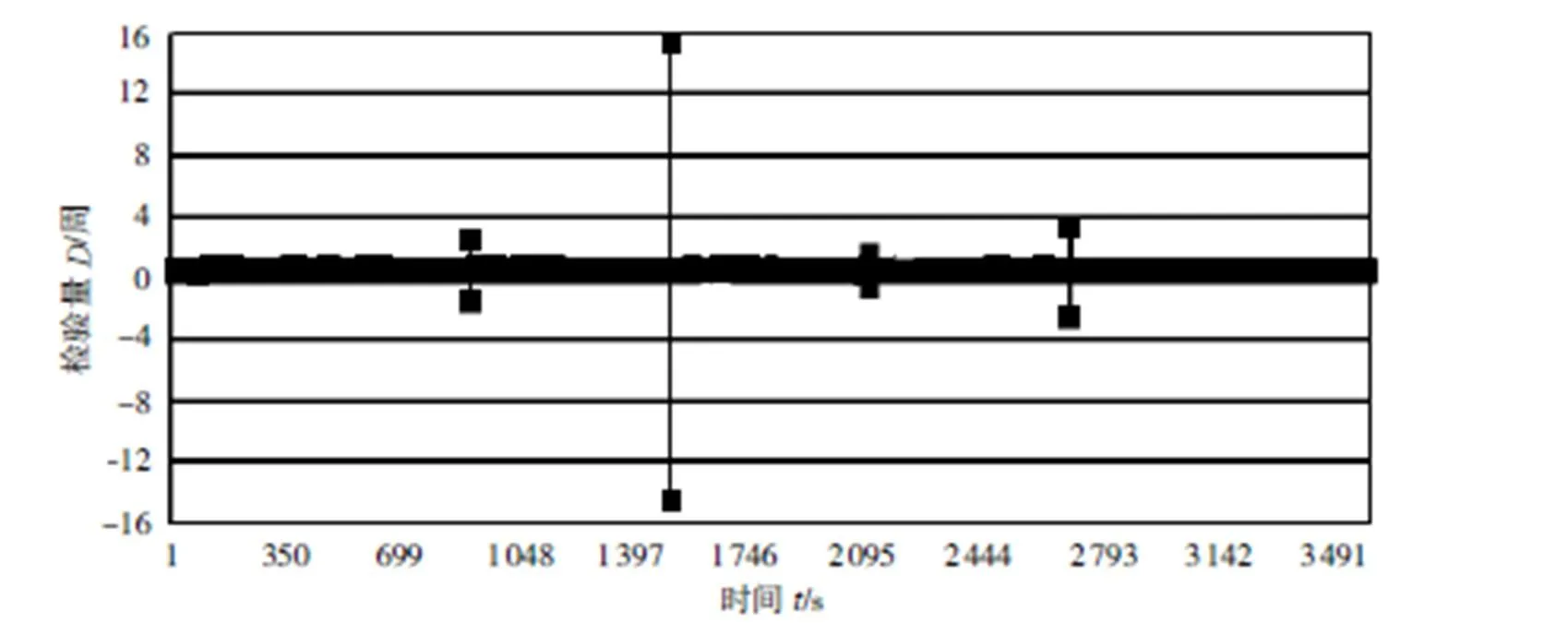
图4 L1载波相位率法得到的检验量D(有周跳)
4 结语
根据以上分析及算例比较,可知双频相位求差法和相位率法探测与修复周跳的特点及利弊。
双频相位求差法探测小周跳的能力较强,其利用伪距差分作为约束条件,解决了周跳解的多值性问题。因此,它不仅能够探测到小周跳,而且可以准确地予以修复;缺点是要求有双频观测数据,不能对单频观测值进行处理。
利用相位率法进行周跳探测,所需数据量小,仅需相邻2个历元的载波观测值,而不需要其他信息,适用于单频接收机;该方法能够锁定发生小至1周周跳的历元并且准确地予以修复。
[1] 何战科, 杨旭海, 李志刚, 等. 利用GPS观测资料解算地球自转参数[J]. 时间频率学报, 2010, 33(1): 69-76.
[2] 徐绍铨, 张华海, 杨志强. GPS测量原理及应用[M]. 3版. 武汉: 武汉大学出版社, 2008.
[3] 黄兵杰, 柳林涛, 高光星, 等. 基于小波变换的GPS精密单点定位中的周跳探测[J]. 武汉大学学报(信息科学版), 2006, 31(6): 512-515.
[4] 魏子卿, 葛茂荣. GPS相对定位的数学模型[M]. 北京: 测绘出版社, 1998.
[5] 刘基余. GPS卫星导航定位原理与方法[M]. 2版. 北京: 科学出版社, 2008.
[6] 贾沛璋, 吴连大. 关于GPS载波相位中的野值周跳与模糊度[J]. 紫金山天文台台刊, 2000, 19(2): 106-110.
[7] 郑作亚, 程宗颐, 黄珹, 等. 对Blewitt周跳探测与修复方法的改进[J]. 天文学报, 2005, 46(2): 216-224.
[8] 王仁谦, 朱建军. 利用双频载波相位观测值求差的方法探测与修复周跳[J]. 测绘通报, 2004(6): 9-11.
[9] 马煦, 常青, 侯俊. 综合利用电离层残差法和载波相位变化率法探测并修复周跳[J]. 电讯技术, 2005, 45(1): 115-119.
[10] 陈蕾, 陈立龙, 李环波. 综合利用载波相位变化率和切比雪夫多项式探测与修复单GPS周跳[J]. 测绘科学, 2010, 35(3): 167-168+175.
[11] 罗伟, 姚宜斌, 宋伟伟. 综合利用多项式拟合和载波相位变化率探测单频GPS周跳[J].全球定位系统, 2007, 32(5): 9-13.
[12] GURTNER M. RINEX: The Receiver Independent Exchange Format Version 2.11[M]. Bern: Astronomical Institute University of Berne, 2007.
Comparison between differenced phase method and phase-rate ethod in detection and reparation of cycle slips
LEI Yu1,2, GAO Yu-ping1,2, LIU Na1,2
(1. National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China; 2. Key Laboratory of Time and Frequency Primary Standards, National Time Service Centre, Chinese Academy of Sciences, Xi′an 710600, China)
There are many methods to detect and repair the cycle slips in GPS carrier data, but none of the methods is perfect. The commonly used methods for detecting and repairing the cycle slips are briefly introduced, and the tests of detecting and repairing the cycle slips have been conducted with the differenced phase method and phase-rate method. The results show that both the two methods not only can exactly detect the epoch when small cycle slips take place, but also can repair the carrier phase value efficiently; however the differenced phase method needs the dual frequency carrier-phase data whereas the phase-rate just needs single frequency data.
cycle slip detection and reparation; carrier-phase; differenced phase; phase-rate
P228.4
A
1674-0637(2011)02-0139-07
2010-10-26
国家自然科学基金资助项目(10573019);中国科学院重要方向资助项目(KJCX2-YW-T12)
雷雨,男,硕士,研究实习员,主要从事高精度GPS时间传递方面的研究。
