铯原子喷泉钟均匀C场的实现
2011-06-30吴长江管勇陈江张辉阮军张首刚
吴长江,管勇,陈江,张辉,阮军,4,张首刚,4
铯原子喷泉钟均匀C场的实现
吴长江1,2,管勇1,陈江1,2,张辉3,阮军1,2,4,张首刚1,4
(1. 中国科学院国家授时中心,西安 710600;2. 中国科学院研究生院,北京 100039;3. 西北大学 光子学与光子技术研究所,西安 710069;4. 中国科学院时间频率基准重点实验室,西安 710600)
C场均匀度是影响铯原子喷泉钟性能的重要因素。为了消除漏磁等对磁场均匀度的影响,加入补偿线圈,通过用最小二乘法计算,逐次得出补偿线圈的个数、位置与电流。实验表明:计算数据与实验结果吻合,得到C场不均匀性小于2nT、长度达48cm的均匀区。
铯喷泉钟;磁屏蔽;最小二乘法
国际单位制的7个基本物理量中,时间是测量最精确的物理量,其测量精度比其他量高4~5个数量级[1]。时间单位“秒”则是将位于海平面上的133铯(133Cs)原子基态的两个超精细能级间在零磁场中跃迁振荡9192631770周所持续的时间定义为1个原子时秒。铯喷泉原子钟是目前复现秒定义的时间频率基准原子钟,具有最高的准确度,用于校准其他类型的原子钟。
喷泉钟的工作过程包括冷原子团的制备、选态、与微波相互作用、光探测等阶段,均要求静磁屏蔽,以消除地磁场对原子能级的扰动,而作为原子与微波相互作用场所的微波腔及原子自由飞行段,要求更是严格,需要多层磁屏蔽,以把外磁场衰减到nT量级或更低。磁光阱磁场和选态腔磁场波动对原子能级的影响同样需要磁屏蔽装置来消除。
喷泉钟微波腔内微波与原子的相互作用,需要在磁屏蔽内部有一个均匀的沿竖直方向的外磁场为原子提供一个量子化轴方向,使原子基态超精细能级发生塞曼分裂,该均匀的沿竖直方向的外磁场称之为C场。然而,由于C场线圈的端口效应及磁屏蔽组件在组装过程中接缝处的漏磁,再加上磁屏蔽材料剩磁的影响,实际的C场并不均匀,因此需要通过在磁屏蔽内部加补偿线圈使C场均匀。本文首先从理论上分析磁场不均匀度对喷泉钟准确度的影响,然后介绍运用最小二乘法,依次计算出补偿线圈个数、位置和电流大小,使C场不均匀性变小,满足喷泉钟工作的需要。
1 C场均匀度要求
在C场作用下,铯原子基态超精细能级跃迁频率,即原子钟的跃迁频率,将会发生改变,称为二阶塞曼频移。微波腔及原子自由飞行段磁场不均匀带来的各点C场频移不同,造成评定该项频移的不确定度增大。
C场产生的二阶塞曼频移为[2]

C场不均匀也使得铯原子Rabi跃迁中心频率与Ramsey跃迁中心频率不一致,2者互相牵引,导致共振跃迁频率移动,相对频移量为[3]:


此外,原子在不均匀磁场运动,也会发生Majorana跃迁,产生频移。对于原子喷泉频标,在相互作用区内,由于C场场强很小,仅约100 nT,不均匀程度也相应减小;又因为采用了高性能的磁屏蔽和补偿线圈,故C场的均匀性非常好,相互作用区内C场分布的最大差值要求小于2nT。另一方面,由于原子喷泉采用冷原子源,束原子运动很慢,速度仅为每秒数米。这样,束原子在运动过程中感受到的磁场变化将非常缓慢。关于Majorana跃迁产生的频移,在磁场无过零点突变情况下,原子经过选态后,Majorana跃迁产生的相对频移在1×10-19以下,可忽略不计[4]。
由以上分析可见,磁场均匀度高低会影响喷泉钟的准确度。为了使C场均匀度符合要求,必须加入补偿线圈补偿由于漏磁、剩磁等因素导致的磁场不均匀问题。
2 磁屏蔽装置
国家授时中心正在研制的铯喷泉原子钟共有4层磁屏蔽,如图1所示。整体为长方体结构,周围由4块屏蔽板包围,上下有2块屏蔽板覆盖,它们组成一个近似封闭的箱体。只是在上屏蔽板中心开一个直径为154mm的孔,以让真空管伸出。最外层屏蔽对喷泉钟整体进行初级磁屏蔽,可减小地磁场1~2个数量级。屏蔽板内以钛板为界分为上下2层,下层悬挂探测区、选态腔和磁光阱,上层放置激励腔和真空筒。激励腔放置于真空筒内。真空筒外包围有3层等间隔磁屏蔽筒,其上下盖均为两半圆对接,中心开孔。内、中屏蔽筒上下盖有外沿,以获得更好的磁屏蔽性能。

图1 喷泉钟上部磁屏蔽示意图
屏蔽材料选用1J85坡莫合金,厚度2 mm,热处理后测试结果为最大相对磁导率133000,与国外及国内较好性能相比有较大差距[5]。由于热处理后屏蔽板和屏蔽筒盖发生变形,发生漏磁,且安装屏蔽板和屏蔽筒时受到多次撞击,根据测量加磁屏蔽前后轴线上磁场的变化情况及由文献[6],[7],[8],[9]中公式计算可知实际的平均相对磁导率不足20 000,影响C场的均匀性。为此,我们采用线圈对C场进行补偿,增加C场的均匀度。
3 地磁场补偿
屏蔽筒内有3种不同的磁场:漏地磁场、磁屏蔽材料产生的剩磁和C场线圈产生的磁场。剩磁可以通过交流大电流退磁方法来降低之,线圈中心区域磁场为均匀磁场,控制电流可使其大小线性变化。要获得均匀C场,就归结为对漏磁场的补偿问题,即通过加补偿线圈,产生均匀磁场。
3.1 漏磁场与线圈磁场的拟合
理论计算[10-11]和实验结果都证实,从屏蔽筒端盖一侧向内产生的漏磁沿轴线方向成指数衰减。磁场函数为
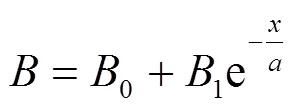
式(3)中,,a均为待定参数,x轴方向为沿真空轴线向下的方向,在真空筒上沿处,x=0。真空筒上沿与外屏蔽筒上盖平齐。当喷泉钟磁屏蔽都安装完毕后,从屏蔽筒上端部向下测量磁场,对数据进行指数拟合,得到a=4.85cm,,也为拟合常数。图2为实验数据与拟合曲线。
为了得到匀强磁场,只需要考虑磁场的指数部分即可。为了补偿指数部分的磁场,在屏蔽筒内部放置线圈,线圈轴线上在自由空间(无屏蔽情况下)产生的磁场为[12]
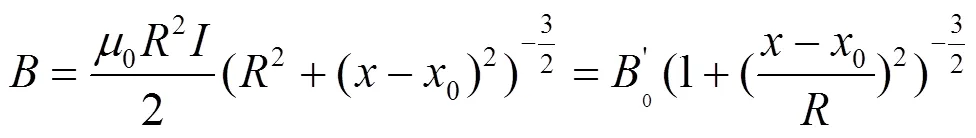
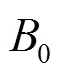

图3 磁屏蔽筒内外线圈磁场拟合
3.2 线圈个数和位置的确定
为了挑选一个合适的线圈,采用最小二乘法,计算如下函数式(5)的最小值

多个线圈放置的具体位置和个数,由最小二乘法和需要确定,求解下列函数式(6)的最小值

计算结果显示:在满足需要时,一组较好的结果是3个线圈,真空筒上两个线圈分别在0cm和7.1cm处,C场筒上线圈在5.3cm处。
3.3 确定线圈电流
确定了线圈个数和位置,下一步就是确定电流的大小。可以用实验分别测定3个线圈在任意给定电流时在真空筒轴线上产生的磁场分布和无电流时的本底值,对下式用最小二乘法计算最小值,可求出各线圈电流值。
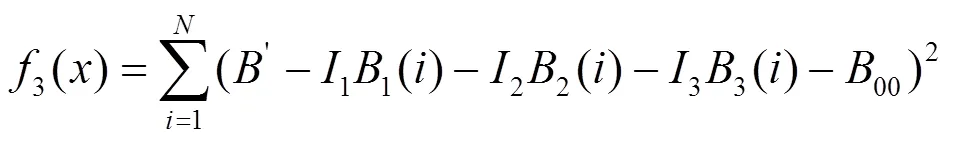
3.4 结果
由以上方法,可得如图4所示的在48 cm长度内变化不超过1.7 nT的均匀区。由计算可知,由C场不均匀性产生的方差为0.11(nT)2,二级塞曼频移为5.1×10-19Hz,由于Rabi跃迁中心频率与Ramsey跃迁中心频率不一致导致共振跃迁频率移动产生的相对频移为1.62×10-17。另外,如果增加线圈个数,精度和长度将会有进一步提高。
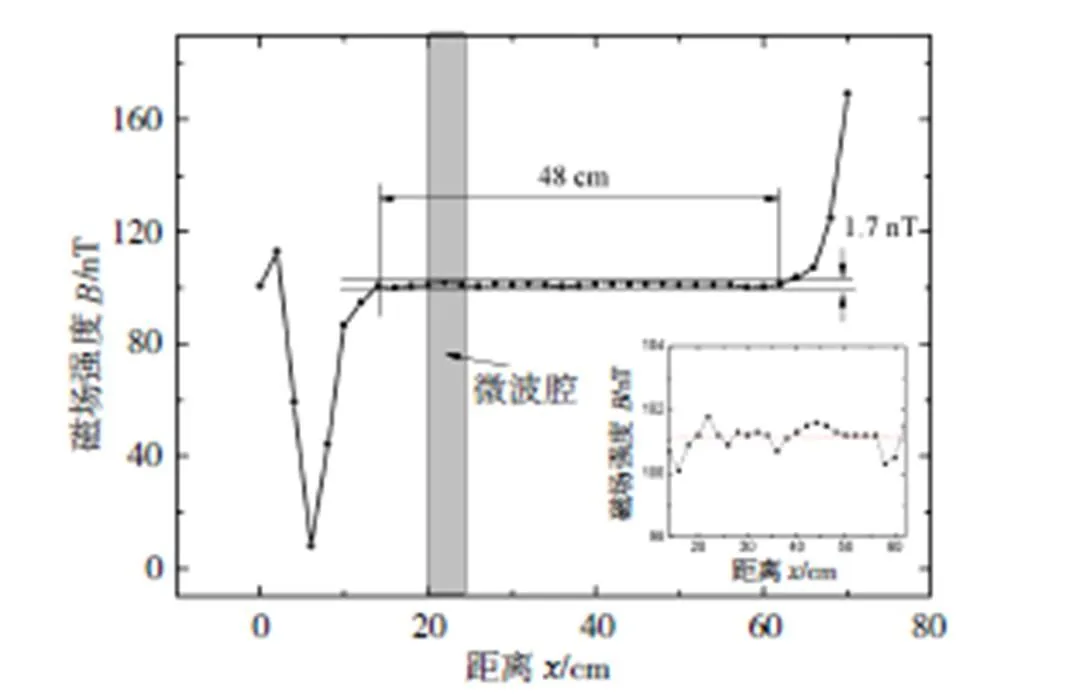
图4 补偿后C场效果图(右下角为局部放大图)
4 结论
为使微波腔附近轴线磁场均匀,加入补偿线圈,应用最小二乘法,依次确定补偿线圈的个数、位置与电流。最后得到在48 cm长度内变化不超过1.7 nT的均匀区。实践证明,理论计算与实验结果相符,该方法为补偿磁屏蔽的不足提供了一个有效的途径。
[1] ZHANG Shou-gang. D′eplacement de fr′equence dˆu au rayonnement du corps noir dans une fontaine atomique `a c′esium et am′elioration des performances de l′horloge[D]. Paris: Universit′e de Paris VI, 2004: 20-23.
[2] KUMAGAI M, ITO H, KAJITA M, et al. Evaluation of caesium atomic fountain NICT-CsF1[J]. Metrologia, 2008, 45: 139-148.
[3] 王义遒, 王庆吉, 董太乾, 等. 量子频标原理[M]. 北京: 科学出版社, 1986: 325-327.
[4] GERGINOV V, NEMITZ N, WEYERS S, et al. Uncertainty evaluation of the caesium fountain clock PTB-CSF2[J]. Metrologia, 2010, 47: 65-79.
[5] 崔雅茹, 刘环, 施源, 等. 提高1J85合金磁性能的最终退火制度的改进[J]. 铸造技术, 2005, 26(12): 1145-1148.
[6] MAGER A. Magnetic shielding efficiencies of cylindrical shells with axis parallel to the field[J]. J. Appl. Phys. 1968, 39: 1914.
[7] FREAKE S M, THORP T L. Shielding of low magnetic fields with multiple cylindrical shells[J]. Rev. Sci. Instrum., 1971, 42(10):1411-1413.
[8] GUBSE R D U, WOLF S A, COX J E. Shielding of longitudinal magnetic fields with thin, closely spaced, concentric cylinders of high permeability material[J]. Rev. Sci. Instrum., 1979, 50(6): 751-756.
[9] DONLEY E A, HODBY E, HOLLBERG L, et al. Demonstration of high-performance compact magnetic shields for chip-scale atomic devices[J]. Rev. Sci. Instrum., 2007, 78(8): 083102-1-7.
[10]MAGER A J. Magnetic shields[J]. IEEE Transactions on Magnetics, 1970, MAG-6(1): 67-75.
[11]CALVO E, CERRADA M, GIL-BOTELLA I, et al. Passive magnetic cylindrical shielding at gauss-range static fields[J]. Nuclear Instruments and Methods in Physics Research A, 2009, 600: 560-567.
[12]赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 1985: 355-357.
[13]克劳斯. 电磁学[M]. 安绍萱, 译. 北京: 人民邮电出版社, 1979: 289.
A realization of uniform C field in caesium atomic fountain clock
WU Chang-jiang1,2, GUAN Yong1, CHEN Jiang1,2,ZHANG Hui3, RUAN Jun1,2,4, ZHANG Shou-gang1,4
(1. National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China; 2. Graduate University of Chinese Academy of Sciences, Beijing 100039, China; 3. Institute of Photonics&Photo-Technology, Northwest University, Xi′an 710069, China; 4. Key Laboratory of Time and Frequency Primary Standards, National Time Service Center, Chinese Academy of Sciences, Xi′an 710600, China)
The performance of the caesium atomic fountain clock is affected by the uniformity of the C field. In order to compensate the uneven magnetic field caused by the leakage in magnetic shielding region, compensation coils are introduced and the number, position and current of the coils are calculated by the least square method. The experimental results agree with the theoretical prediction and an uniform magnetic-field of 48cm with a fluctuation of less than 2 nT is obtained.
caesium fountain clock; magnetic shielding; least squares
TM935.11+5
A
1674-0637(2011)02-0081-06
2011-03-21
中国科学院大科学装置开放资助项目(Y005DK1101);中国科学院“西部之光”人才培养计划资助项目(0811YR3101);国家授时中心知识创新工程青年人才领域前沿项目专项资助课题(0700-YR2S01)
吴长江,男,博士研究生,主要从事量子频标研究。
