三容水箱液位控制系统的设计与仿真

冯鹏辉，谭 兮，刘国营

（湖南工业大学 电气与信息工程学院，湖南 株洲 412008）

三容水箱液位控制系统是工业生产过程中多容流量对象的抽象模型，具较强的代表性，可模拟工业生产过程中一阶或多阶次、线性或非线性、单容或多容、耦合或非耦合等特性，以判别或验证各种控制策略性能的优劣。因而，对三容水箱的控制系统进行研究有重要的理论意义和实际应用价值。

本文拟在分析三容水箱液位控制系统结构和工作机理的基础上，建立该系统结构的非线性模型；采用NI公司PCI-6251数据采集卡[1]和LABVIEW图形化开发界面，设计三容水箱液位控制系统的硬件和软件，并采用人机交互界面对控制过程进行监控和动态模拟，以验证本设计的可靠性。

1 液位控制系统结构及数学模型

三容水箱液位控制系统由水箱主体、差压变送器、气动调节阀、电磁阀、流量传感器、电气转换器、空气压缩机、水泵、多功能采集卡、计算机等组成，硬件结构示意图见图1。

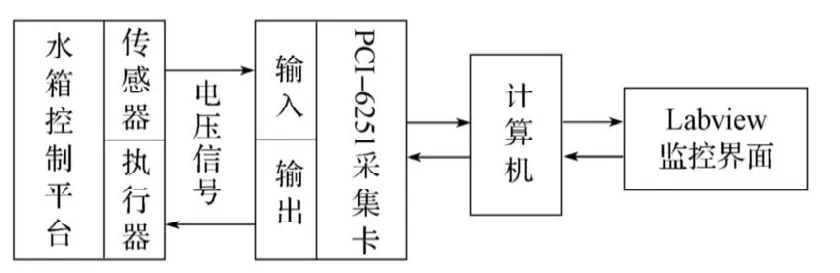
图1 系统结构图Fig.1The chart of system structure

三容水箱的控制系统首先通过差压变送器测量3号水箱的液位，再通过采集卡将3号水箱的液位信号送入计算机，并通过计算机运算处理得到电磁阀开度的实时控制值。最后，通过PCI-6251采集卡的输出端子，将所得控制值送给控制阀，以控制给水流量，从而实现对3号水箱的水位控制。水箱控制对象模型[2]如图2所示。

图2 三容水箱实验模型Fig.2Three-tank experimental model

对图2所示模型进行数学分析，可得该系统的动态方程[2]为：

上式中：C1，C2和C3分别为3个水箱的液容，且C1=C=166 585 mm3，C=169 510 mm3；,,32分别为3个水箱的出水流量，由所设置的阻力板流量特性决定。

分析单个水箱，取阻力板底边直线为x轴，底边中点垂直向上为z轴，非线性阻力板结构见图3。

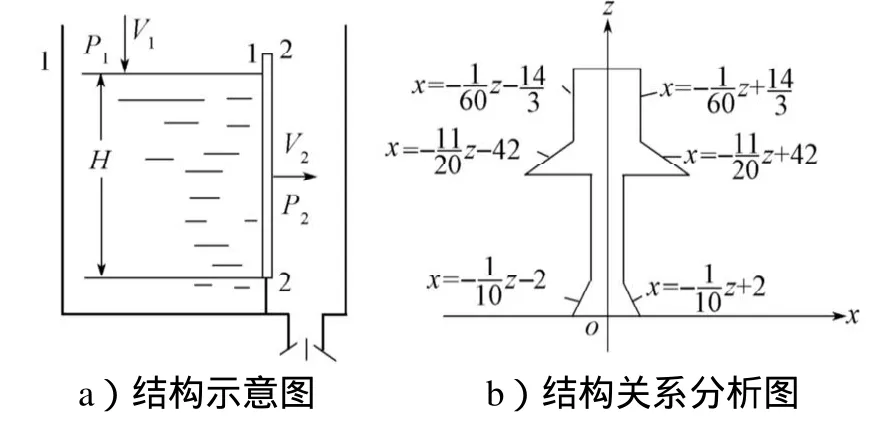
图3 非线性阻力板结构图Fig.3The structure of non-linear resistant plate

由理想伯努力方程可得

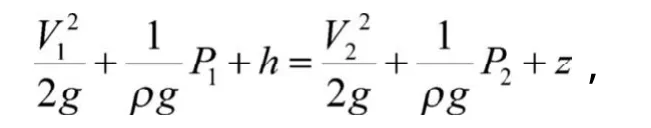
由于P1=P2，/(2g)相对于/(2g)很小，可忽略，故可得。

对图2所示模型建立直角坐标系，实际液位高度为h ，取z 为积分变量，它的变化区间为[ 0, h]，采用定积分元素法可求得水箱不同液位高度h时流过阻力板的液体流量Q。其计算式为：

积分可得：

由于实际的液体有黏性，在流动过程中有能量损失，所以进行流量计算时，需加入修正系数β。笔者通过多次试验，最终确定β的近似值如下：

根据以上分析，我们可在MATLAB/Simulink环境下，结合M函数，建立如图4所示的三容水箱控制系统仿真模型。其中，进水阀门最大比例度对应流量Qmax，其值为233 219 mm3/s。

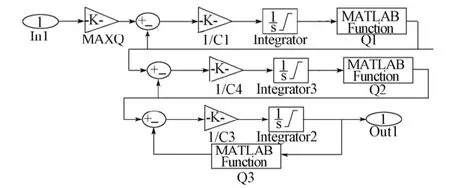
图4 三容水箱仿真模型Fig.4 Three-tank simulation model

2 PID参数整定

因三容水箱控制系统结构的数学模型具非线性特点，常规PID（proportion integration differentiation）算法只使用一组PID参数，不能满足本系统动、静态性能的需要，故可对其划分控制区间，采用多组PID参数进行控制，从而提高控制效果。

通过对控制系统模型的分析，可得水箱的控制系统流量与液位曲线图。通过对该曲线进行分析，可将曲线近似分成斜率相等的4段，即可将水箱控制过程划分为4个控制区间，分别在各区间中找出一个关键点进行人工PID整定，故可得到4组PID参数（见表1），PID整定效果如图5所示。

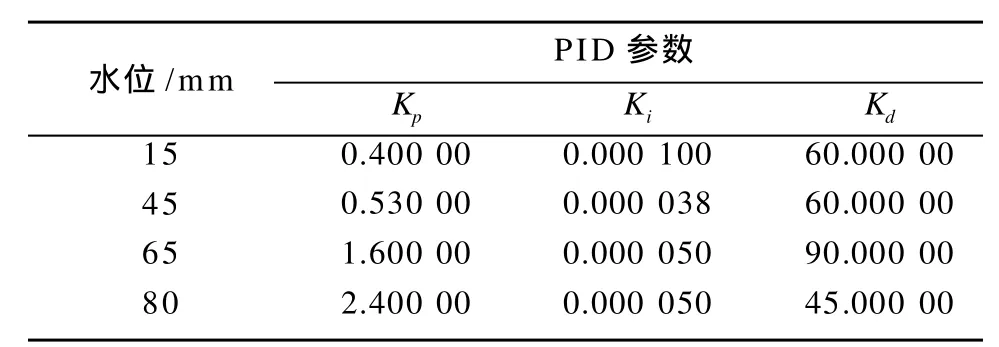
表1 各区间PID参数整定结果Table1 The tuning results of parameters PID

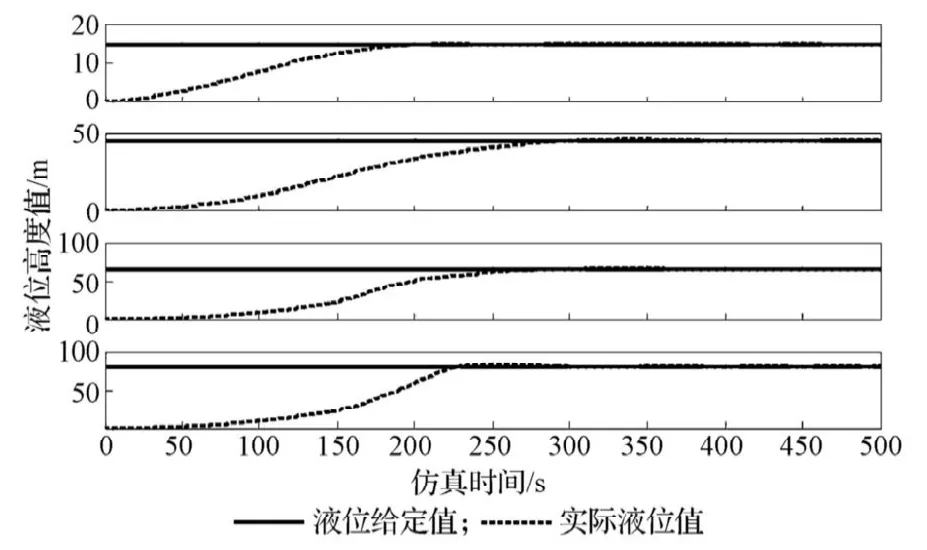
图5 PID 整定曲线Fig.5 PID setting curves

由图5所示仿真控制过程曲线可看出，控制系统在液位高度为15, 45, 65, 80 mm处的调整时间分别为250, 350, 310, 275 s，最大超调量分别为3.5%, 4.5%, 3.8%,3.7%，无静差。这一结果表明，PID参数整定的效果均达到本系统的设计要求。

3 控制算法实现

3.1 非线性变参数PID

常规PID算法较简单，且易于实现，但由于本控制系统的流量随液位变化造成的非线性问题，使得常规PID控制性能不佳，而采用分段变参数PID[3]可在不同控制区域中变化参数，能较好地解决这一问题。因此，本设计中采用非线性的分段变参数PID控制方法，其仿真结构见图6。

图6 非线性变参数PID仿真模型Fig.6The simulation model of nonlinear variable parameters PID

采用分段变参数PID仿真分析时，应使给定信号处于不同水位，观察系统的稳态性能；而水位变化时，观察系统的动态性能，结果见图7。由图7可看出，液位在小范围内变化时，其给定值和实际液位值的跟随性较好，可取得较好的控制效果；但水位在大范围内变化时，会出现较大的超调，且水位下降时，系统响应速度过慢。通过分析上述控制问题，可采用改进PID控制算法以达到更好的控制效果。

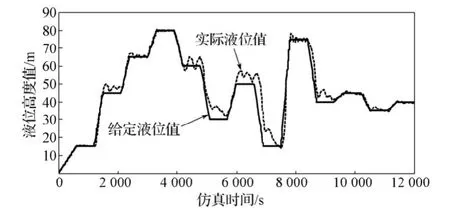
图7 非线性变参数PID响应曲线Fig.7Response curve of nonlinear variable parameters PID

积分作用可消除静态误差，提高系统精度，但在液位上升或下降阶段，短时内会有较大偏差，会使得PID运算的积分积累，引起系统较大地超调，为此，引入对变积分的PID控制算法、抗积分饱和的PID控制算法与分段式PID相结合，以减小超调，提高系统的响应速度。利用S函数编写变积分模块和抗积分饱和模块。变积分PID积分项系数如下：

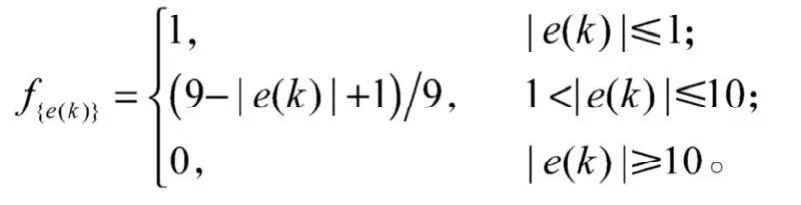
变速积分PID通过改变积分系数来改变系统偏差：系统偏差越大，则积分越慢，反之则越快。抗积分饱和PID是在系统存在一个方向上偏差时，PID控制器的输出由于积分作用的不断累加而加大，从而导致执行机构达到极限位置。各算法的液位控制仿真如图8所示。

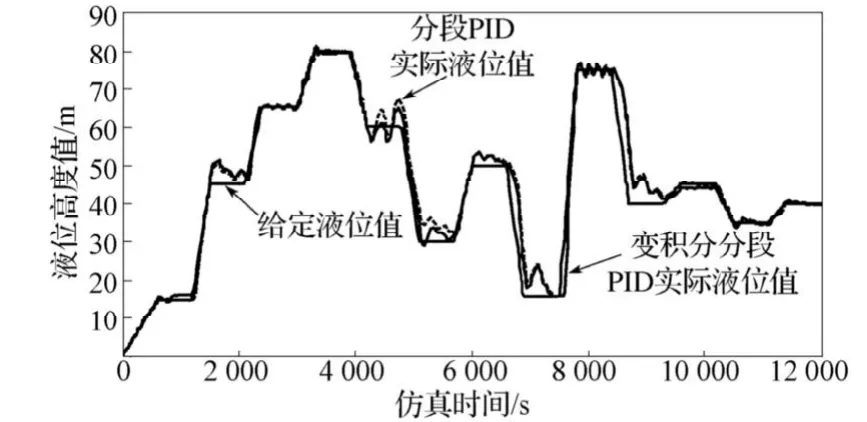
图8 非线性变参数PID优化比较Fig.8The comparison of nonlinear variable parameters PID optimization

3.2 非线性变参数自适应模糊PID

由于水箱流量随水位变化时，具有非线性、大惯性和控制对象参数变化等问题，传统的改进PID控制策略不能达到很好的效果。模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的计算机智能控制。自适应模糊控制运用现代控制理论，在线辨识对象特征参数，实时改变其控制策略，且不依赖对象的数学模型，对象在大范围内变化时，系统仍可自动地工作于最优或接近于最优的运行状态，因此，本设计中采用自适应模糊控制。自适应模糊PID的结构如图9所示。

利用人工智能方法，总结操作人员的经验并存入知识库，建立合适的控制规则，设计模糊控制器。同时，利用分段变参数实现控制系统PID参数的粗调，自适应模糊控制器通过不断辨识当前的对象特征来进行PID参数精调，最终合成一组最佳PID参数，保证液位给定大范围变化情况下的快速性和准确性。本研究所设计的控制模型如图10所示。

图9 自适应模糊PID控制结构图Fig.9The control structure of adaptive fuzzy PID

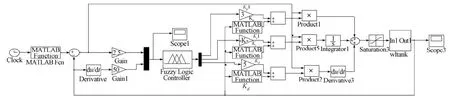
图10 非线性变参数模糊PID仿真图Fig.10The simulation chart of nonlinear variable parameters fuzzy PID

三容水箱控制系统中采用二维输入、三维输出的模糊控制器，将水位偏差变化量和水位偏差变化率作为输入，ΔKp,ΔKi,ΔKd作为模糊控制器的输出。论域分别为 [-3, +3]，[-3, +3]，[-0.3，+0.3]，[-0.06，+0.06]，[-3，+3]，模糊语言变量均使用7个语言变量值[NB，NM，NS，Z，PS，PM，PB]来表示。隶属函数均采用工程中常用的等分三角形隶属函数，液位偏差E的隶属函数如图11所示。

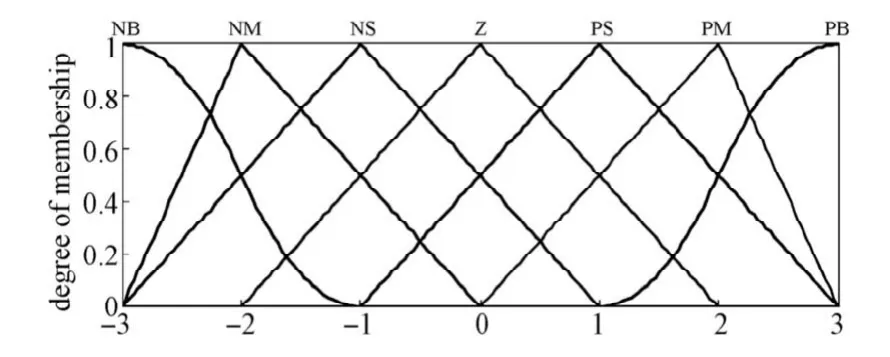
图11 输入变量的隶属函数Fig.11Membership function of input variables

模糊规则表由手动操作人员长期积累的经验得出，其中ΔKp的模糊规则表见表2。

表2 模糊控制规则表Table 2The table of fuzzy control rules

通过分析实际输入输出与模糊论域之间的关系，E的量化因子取2.5，EC的量化因子取50，ΔKP的比例因子为3，ΔKi的比例因子为0.000 2，ΔKd的比例因子为1.3，系统的仿真结果如图12所示。从图12中可看出，通过将自适应模糊PID与分段变参数PID结合，使得系统具有响应速度更快、更准确，超调更小，振荡更少，鲁棒性更强的特点。

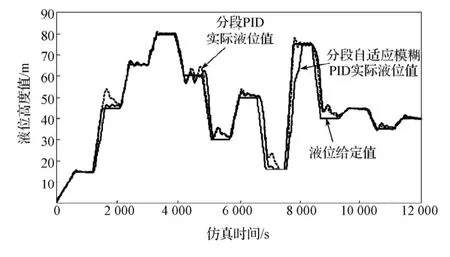
图12 非线性变参数模糊PID与变参数PID仿真比较Fig.12The simulation comparison of nonlinear variable parameters fuzzy PID and variable parameter PID

4 Labview控制程序及监控界面

4.1 数据采集

NI PCI-6251是一款M系列的多功能智能数据采集和智能设备，带有16路模拟输入和2路模拟输出通道，同时还提供24门数字I/O，32位计数器。三容水箱控制系统采用其中的两路模拟输入、一路模拟输出。

模拟输入的连续采集驱动程序见图13。

图13 模拟输入的连续采集的驱动程序Fig.13The analog input of continuous acquisition driver program

4.2 控制程序

本设计中，利用Labview[4]控制仿真设计工具包和模糊逻辑工具包编写控制程序，其可模拟三容水箱控制系统的动态过程。其中，高级控制算法和水箱控制对象建模[5]，通过MathScript[4]节点和创建子程序来实现。通过控制程序与采集驱动程序结合可以对数据进行实时处理，实现对控制过程的监控。

水箱模拟控制程序如图14所示。

图14 水箱动态模拟控制程序Fig.14The dynamic simulation program of tank-level

4.3 监控界面

监控界面实时监控水箱的整个控制过程，并可设定水箱的工作方式和3号水箱的水位，显示各水箱液位的变化趋势。通过监控界面选项板可使控制系统工作在不同的工作状态。模拟监控界面见图15。

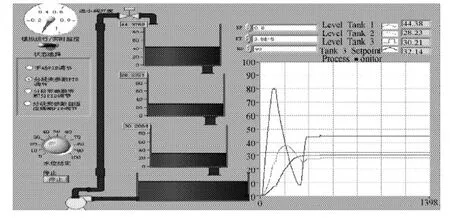
图15 模拟控制界面Fig.15The main interface of simulation control

动态模拟工作方式可进行半实物仿真，实时观察3个水箱的水位变化，其中的趋势图可记录水箱水位的变化，当水位设为30 cm时，由水位变化趋势图可观察到水箱的液位约在300 s左右达稳定，3号水箱液位偏差在1 cm左右，动态模拟控制效果与MATLAB仿真分析结果一致。其中，稳定后3个水箱的水位值与实测值接近，具有较好的半实物仿真效果。

5 结语

通过分析三容水箱液位控制系统的结构和运行过程，利用MATLAB 建模仿真研究系统的运行特点，将变参数PID与自适应模糊PID结合，设计出非线性变参数自适应模糊PID控制器，仿真效果较好。在此基础上，利用虚拟仪器软件结合控制工具包，设计了水箱控制系统的控制程序和人机交互界面，最终完成了整个控制系统的设计，仿真结果表明，系统在该设计条件下取得了较好的控制效果。

[1]蔡文智，陈德为.LabVIEW及其在电气控制方面的应用现状[J].电气开关，2007(5)：46-48.Cai Wenzhi，Chen Dewei.LabVIEW and Its Application in Electrica1 Contro1[J].Electric Switchgear，2007(5)：46-48.

[2]赵 科，王生铁，张计科.三容水箱的机理建模[J].控制工程，2006，13(6)：521-524.Zhao Ke，Wang Shengtie，Zhang Jike.Mechanism Modeling for Three-Tank Water[J].Control Engineering of China，2006，13(6)：521-524.

[3]刘金琨.先进PID控制及其MATLAB仿真[M].北京：电子工业出版社，2003：115-129.Liu Jinkun.Advanced PID Control and MATLAB Simulation[M].Beijing：Electronic Industry Press，2003：115-129.

[4]陈锡辉，张银鸿.LabVIEW 8.20程序设计从入门到精通[M].北京：清华大学出版社，2007：32-266.Chen Xihui, Zhang Yinhong.LabVIEW 8.20 Program Design from Entry to Master[M].Beijing：Tsinghua University Press，2007：32-266.

[5]吴异卉，王启志.基于LabVIEW的模型参考自适应控制的实现[J].计算机技术与发展，2008，18(11)：180-182.Wu Yihui，Wang Qizhi.Realization of Adaptive Control Reference Model Based on LabVIEW[J].Computer Technology and Development，2008，18(11)：180-182.