甲醇-四氟丙醇汽液相平衡研究
2011-06-30吕克新刘登华
周 涛,吕克新,刘登华,孙 超,高 军
(1.中南大学 化学化工学院,湖南 长沙 410083;2.潍坊科技学院 化学工程学院,山东 寿光 262700;3.山东科技大学 化学与环境工程学院,山东 青岛 266510)
0 引言
在化学工业中,蒸馏、吸收过程的工艺和设备设计都需要准确的汽液平衡[1]数据,此数据对提供最佳的操作条件,减少能源消耗和降低成本等,具有重要的意义。尽管有许多体系的平衡数据可以从资料中找到,但是这些数据大多是在特定的温度和压力条件下得到的,因而不能满足实际应用要求。
随着科学技术的迅速发展,以及新产品、新工艺的开发,许多物系的平衡数据亟待测定,因而需要通过试验测定以满足工程计算的需要。此外,在溶液理论研究中,研究者们提出了各种各样的描述分子间相互作用的模型[2],准确的平衡数据是对这些模型的可靠性进行检验的重要依据。但在已有的相关报道中,尚未见甲醇-四氟丙醇[3]二元体系汽液相平衡数据的相关报导,因此,本研究拟对该体系的汽液相平衡状况进行探讨,以期为化工理论研究及实际应用提供相应的基础数据。
1 试验部分
1.1 试验试剂
甲醇:分析纯,纯度≥99.7%,由莱阳市康德化工有限公司生产。并将其精馏,取中间60%的馏分备用,且气相色谱分析显示该馏分无杂质峰。
四氟丙醇:分析纯,纯度≥99.962%,由青岛三江化工实业有限公司生产。
1.2 试验仪器
本试验中的主要仪器如下:精密电子天平,FA2104型,由上海精科天平厂生产;精密温度计,精度为0.01 ℃,购于市场;汽液平衡釜,TJDX型,由天津大学生产;超级恒温水浴,501 型,由上海实验仪器有限公司生产;单目阿贝折射仪,2AWJ型,由上海实验仪器有限公司生产。
1.3 试验步骤
1.3.1 标准曲线的测定
首先,在常压(101.325 kPa)、温度为30.0 ℃条件下,将甲醇与四氟丙醇按比例配制成不同组成的甲醇-四氟丙醇溶液。然后,用单目阿贝折射仪测定各组溶液的折射率,再确定溶液浓度比与折射率的关系,即可得到该压力与温度下待测溶液浓度比与折射率的标准曲线。
1.3.2 汽液相平衡试验
在双循环汽液平衡釜[4]的沸腾室内加入甲醇-四氟丙醇溶液。接通加热电源,调节加热电压为150~200 V,于常压下开始加热,并在平衡釜上方的冷凝管中通入冷却水。将平衡釜缓慢升温,至釜内液体沸腾。此时,汽相冷凝液开始出现,继续加热体系,直到冷凝液开始回流。
试验初始阶段中,平衡温度计的读数不断变化,此时应调节体系加热量,使冷凝液生成的速度控制在每分钟60滴左右。最终使平衡温度趋于稳定,体系汽液相平衡的主要标志由平衡温度的稳定加以判断。试验中,体系经加热1/2~1 h后稳定,此时应记录体系的平衡温度及气相温度,并读取大气压力计上的大气压力。同时,分别用干燥滴管吸取气相冷凝样品与液相样品各1 mL,用单目阿贝折射仪测定平衡汽液相样品的折光率,由甲醇-四氟丙醇标准曲线得到样品汽、液相的组成,每一组样品分析2次,分析误差应小于0.5%。再以相同的方法测另一组样品,得到一系列不同组成的甲醇-四氟丙醇汽、液两相的折光率,从而得到不同组成溶液的恒压汽液相平衡数据。
2 结果与讨论
2.1 组成-折射率数据
在常压(101.325 kPa)、温度为30 ℃试验条件下,所测得的甲醇-四氟丙醇二元体系的组成-折射率数据曲线见图1。
由图1可得,该试验条件下,甲醇-四氟丙醇二元体系中甲醇的质量分数与折射率的拟合曲线为:
y=0.006x2+0.001x+1.319,
上式中:x为甲醇的质量分数;y为体系折射率。
该式可用于计算汽液相平衡实验中汽、液两相甲醇的质量分数。
2.2 相平衡数据
将本试验所测得的数据(参见表2和表3)进行拟合,可得如图2所示的甲醇-四氟丙醇二元体系在常压下的汽液平衡数据相图。
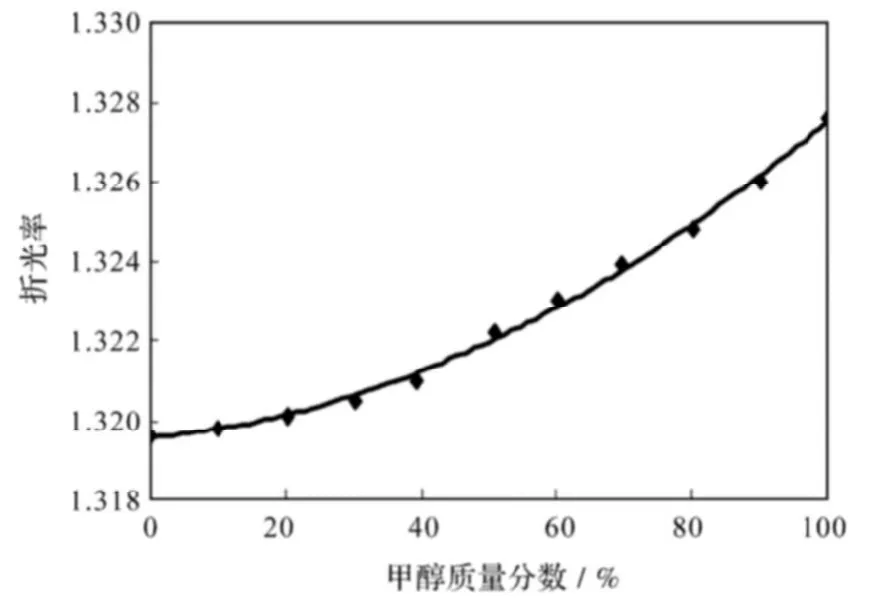
图1 30.0℃时甲醇-四氟丙醇的折光率曲线Fig.1The refractive index curve for Methanol-TFP at 30℃

图2 常压下甲醇-四氟丙醇的汽液平衡Fig.1The vapor-liquid equilibrium of Methanol-TFP at atmospheric pressure
2.3 热力学一致性检验
对于二元系统,一般用Gibbs-Duhem方程[2]进行热力学一致性检验,方程为:
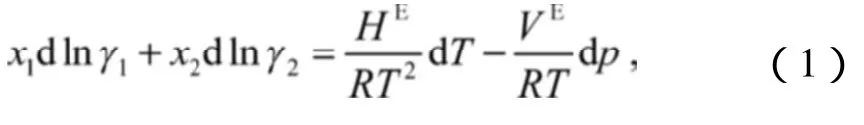
式(1)中:γ1为组分1的液相活度系数;
γ2为组分2的液相活度系数;
HE为体系超额焓;
R为通用气体常数;
VE为体系超额摩尔体积。
等压条件下,上式右边的第二项等于零。则式(1)变为:

由于式(2)中HE不可忽略,因此不易直接积分。所以本文采用Herington的半经验法来检验二元等压数据的热力学一致性。
D=(|SA-SB)/(SA+SB)×|100。
式中A,B分别为曲线在横轴以下和以上的区域,参见图3。
再将所得D值与另一数量J比较,J为和组分的沸点范围有关的变量,且
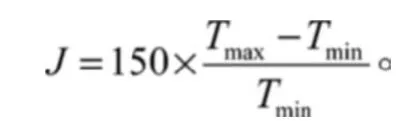
判别标准为:当D
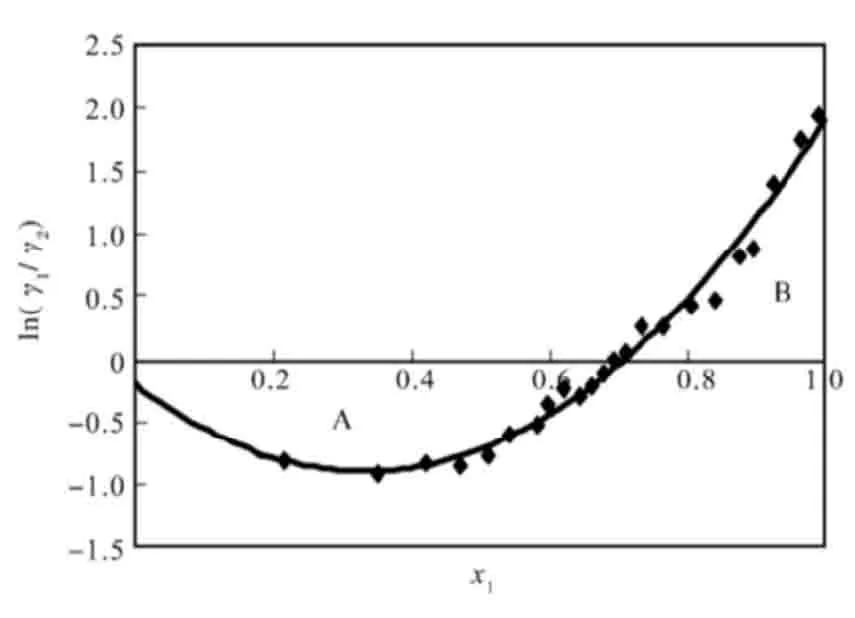
图3 甲醇-四氟丙醇常压汽液相平衡实验数据热力学一致性校验Fig.3The thermodynamic consistency test for methanol-TFP system
由图3可得出其拟合的曲线为:

D-J=29.14-20.01=9.13<10。
因此,试验测定的甲醇-四氟丙醇体系汽液相平衡数据符合热力学一致性要求。
2.4 汽液平衡数据的关联
本研究拟采用Wilson模型[5-7]和NRTL模型[8-10]对甲醇-四氟丙醇二元体系的汽液相平衡数据进行关联分析。
对于二元系统,其Wilson方程为:
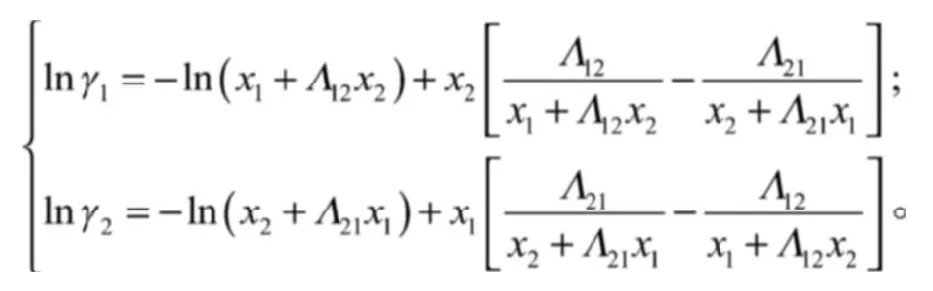
其中:
对于二元系统,其NRTL方程为:
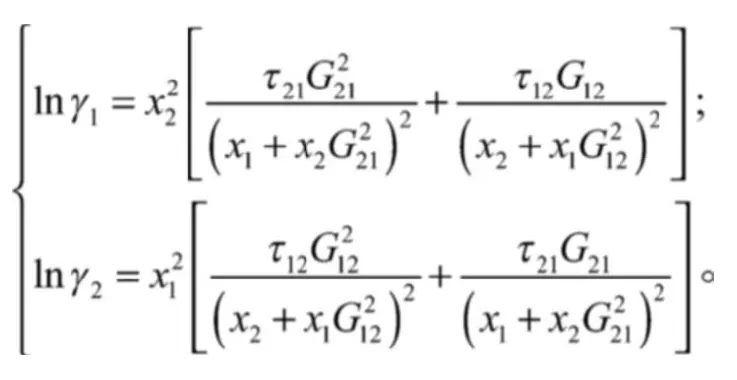
上式中:
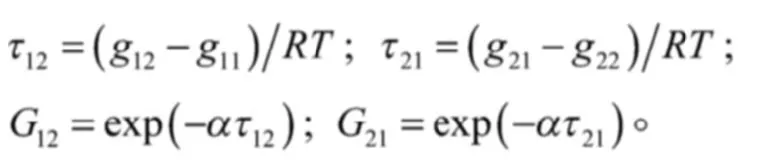
根据以上方程,经计算可以得出甲醇-四氟丙醇二元体系在Wilson模型中和在NRTL模型中的能量参数,具体数据见表1。

表1 甲醇-四氟丙醇能量参数Table1 The energy parameters of methanol-TFP system
将试验所得甲醇-四氟丙醇二元体系常压下的汽液相平衡值与Wilson模型计算值进行比较,所得结果如表2所示。
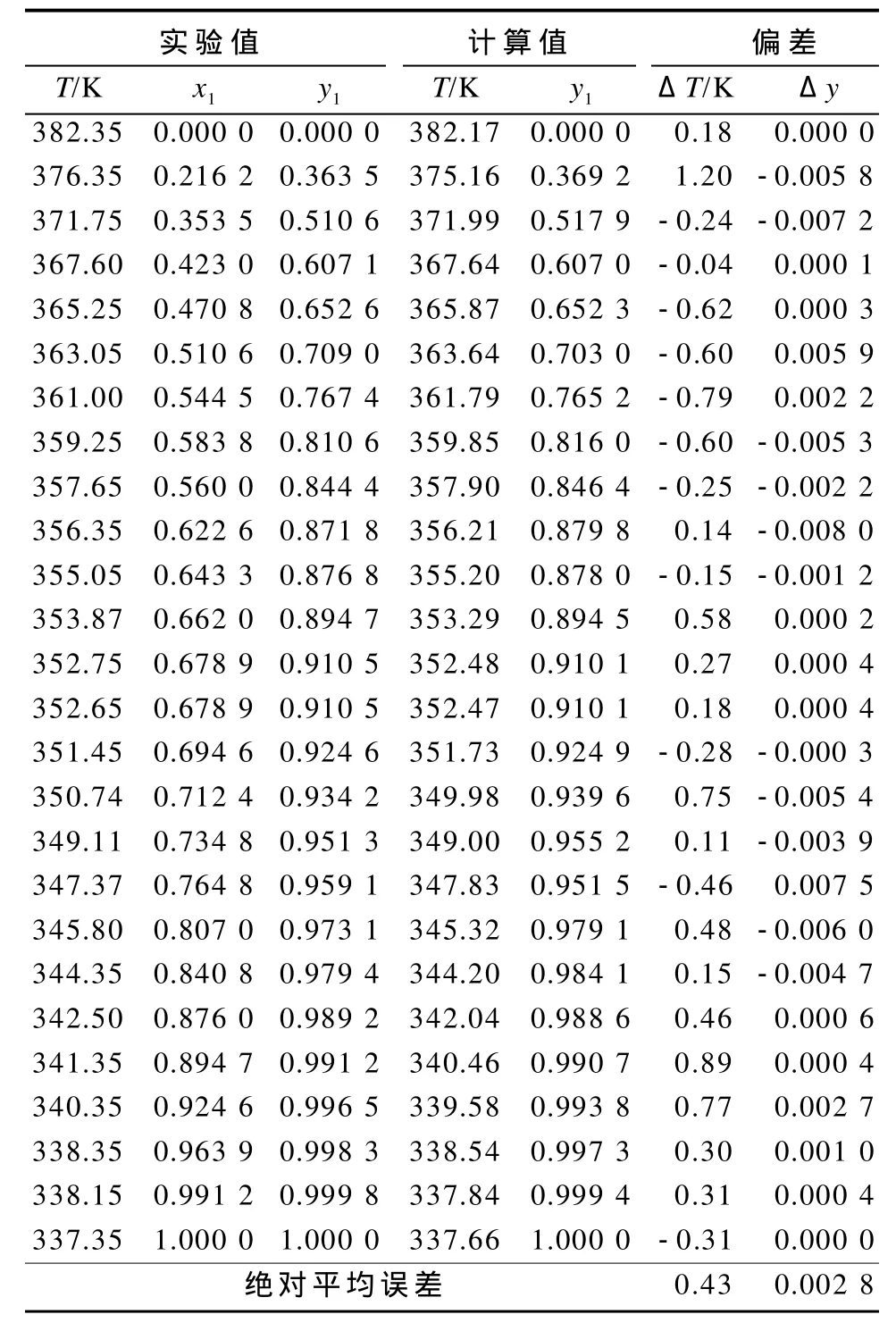
表2 甲醇-四氟丙醇体系常压下汽液相平衡实验值与Wilson模型计算值比较Table2 Comparison of VLE data and the calculated data of Wilson model for methanol-TFP system at atmospheric pressure
由表2可以看出,甲醇-四氟丙醇二元体系温度的绝对平均误差为0.43 K,汽相组成绝对平均误差为0.002 8。这一结果表明,试验所得数据与Wilson模型推导的数据吻合度较高。因此,采用实验回归的Wilson相互作用能量参数预测甲醇-四氟丙醇二元体系的液汽相平衡数据是可靠的。
将试验所得甲醇-四氟丙醇二元体系常压下的汽液相平衡值与NRTL模型计算值进行比较,所得结果如表3所示。
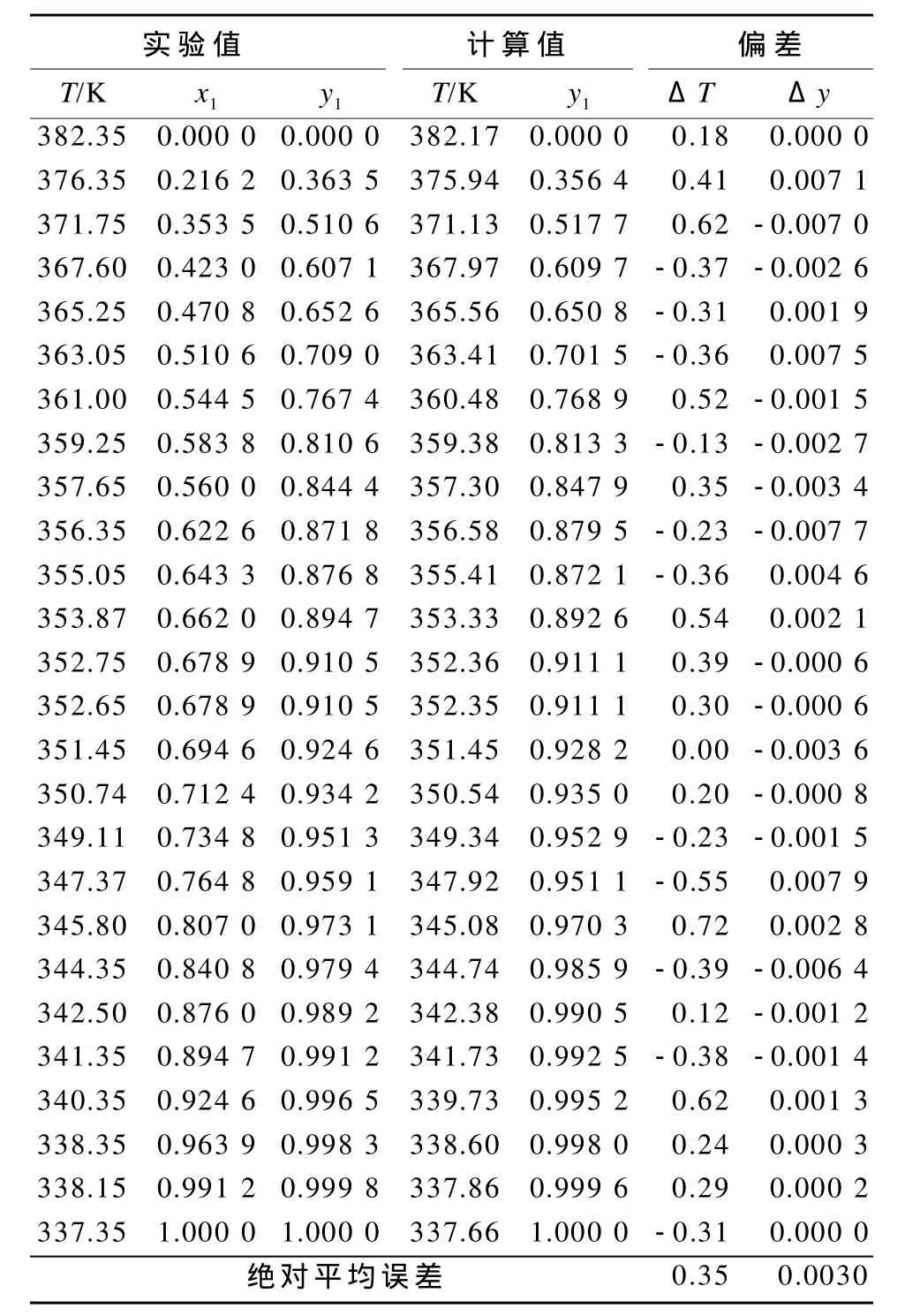
表3 甲醇-四氟丙醇体系常压下汽液相平衡实验值与NRTL模型计算值比较Table 3Comparison of VLE data and the calculated data of NRTL model for methanol-TFP system at atmospheric pressure
由表3可以看出,甲醇-四氟丙醇二元体系的温度绝对平均误差为0.35 K,汽相组成绝对平均误差为0.003 0。这一结果表明,试验所得数据与NRTL模型推导的数据吻合度较高。因此,由实验回归的NRTL模型能量参数预测甲醇-四氟丙醇二元体系的相平衡数据是可靠的。
3 结论
本文测定了常压下甲醇-四氟丙醇二元体系的汽液相平衡数据,并对所得数据进行了热力学一致性检验,得到了如下结论:
1)测得了各甲醇-四氟丙醇二元体系于101.33 kPa下的汽液相平衡数据。采用Herington面积法对试验数据进行热力学一致性检验的结果表明,所测得的该二元体系的汽液相平衡数据均符合热力学一致性要求。
2)选用Wilson模型和NRTL模型对试验数据进行关联度分析,得到甲醇-四氟丙醇Wilson模型的能量参数(λ12-λ11)/R为-223.99 K,(λ21-λ22)/R 为 174.12 K ;NRTL模型的能量参数(g12-g11)/R为478.41 K,(g21-g22)/R为-624.15 K,且试验所得数据与模型计算数据能较好地吻合。
[1]Abbott M.Low-Pressure Phase Equilibria: Measurement of VLE[J].Fluid Phase Equilibria, 1986,29:193-207.
[2]金克新,赵传均,马沛生.化工热力学[M].天津:天津大学出版社,1990:183-188.Jin Kexin, Zhao Chuanjun, Ma Peisheng.Chemical Engineering Thermodynamics[M].Tianjin: Tianjin University Press, 1990:183-188.
[3]陈文华.四氟丙醇[J].精细与专用化学品,2002(8):21-22.Chen Wenhua.Four Fluorine Propanol[J].Fine and Specialty Chemicals,2002(8):21-22.
[4]王 琦,陈庚华,韩世钧.双循环加压气液相平衡装置的建立与校核[J].石油学报:石油加工,1988,4(2):50-56.Wang Qi, Chen Genghua, Han Shijun.Establishment and Tests of Doube-Circulating Vaporliquid Equilibrium Equipment under Pressure[J].Acta Petrolei Sinica:Petroleum Processing Section,1988,4(2):50-56.
[5]金彰礼,邱道发.用Wilson方程计算汽相组分活度系数[J].化学工程,1983(1):27-33.Jin Zhangli, Qui Daofa.The Calculation of Vapor Activity Coefficient by WILSON [J].Chemical Engineering:China,1983(1):27-33.
[6]胡福欣.二元体系气液平衡的测定和关联[J].信阳师范学院学报:自然科学版,1996,9(1):53-56.Hu Fuxin.Measurement and Correlation of Vapor-Liquid Equilibrium Data for the Binary Systems[J].Journal ofXinyang Teachers College:Natural Science Edition,1996,9(1) :53-56.
[7]谷里鹏.WILSON参数的快速求取法[J].化工进展,2003,22(增刊1):262-265.Gu Lipeng.A Simplified Method to Acquire the Parameters of WILSON[J].Chemical Industry and Engineering Progress,2003,22(S1):262-265.
[8]Li Chunxi,Wang Wenchuan.A Surface Tension Model for Liquid Mixtures Based on NRTL Equation[J].Chinese Journal of Chemical Engineering, 2001,9(1):45-50.
[9]蒋晓伟,汪 洋,关春欣.NRTL方程与SRK方程在非理想体系的气液平衡计算[J].化工设计,2007,17(5):11-15.Jiang Xiaowei,Wang Yang,Guan Chunxin.Calculation forVapor-Liquid Phase Equilibrium of Nonideal System with NRTL and SRK Equation[J].Chemical Engineering Design,2007, 17(5):11-15.
[10]Peng D Y,Robinson D B.A New Two-Constant Equation of State[J].Ind.Eng.Chem.Fundam.,1976,15:58-64.
