周期性倾斜边狭缝阵列金膜结构的超强透射

周 昕，李雪勇，易秀英，陈星辉

（1.湖南工业大学 理学院，湖南 株洲 412007； 2.湖南科技职业学院 机电系，湖南 长沙 410118）

0 引言

自Ebbesen等人[1]开创性的研究工作以来，通过亚波长金属小孔或狭缝阵列的超强光透射现象已成为研究热点，这是由于其展示出的独特物理性质及其在近场显微[2]、光调控、表面等离子体器械[3]、平板显示[4]等方面的潜在应用所引起的。Martin-Moreno等人[5]指出，超强透射是由于金属表面等离子体激元隧穿引起的。许多研究者[6-7]也认为：超强透射与因周期性结构而在金属-介质表面所激发的表面等离子体激元（surface plasmon polaritons，SPPs）和入射光的共振耦合作用密切相关。研究还表明：周期性亚波长金属孔阵列的超强透射现象受孔的形状和大小[8-9]、金属种类[10]、电介质-金属-电介质结构的对称性[11-12]等因素影响，且这个现象存在于较宽的波长范围内，如微波波段、红外波段、真空紫外波段等。且理论和实验证实较强的透射共振也常伴随着金属表面局域电场的增强[13]。由于其在纳米光学及量子光学等领域具有广泛的应用前景，亚波长周期性金属阵列结构的超强透射特性引起了人们极大的关注。

目前，对亚波长周期性金属阵列结构的研究工作主要集中在单层和同向性结构，双层及多层结构虽已进行研究，但还不够全面，且物理机制还没有完全解释清楚。事实上，在复合周期结构中，多个表面等离子体波之间的相互作用、相位分布等有许多不同于单元胞周期结构的特征[14-15]。特别是人们发现：如果把2层金属纳米狭缝放置在较近位置，透射谱特征和电磁场将发生改变，这提供了控制倏逝场耦合的方法，从而获得了单层薄膜所不具有的新颖光学性能[16-17]。本文利用时域有限差分法（finitedifference time-domain，FDTD）研究双层亚波长具有周期性倾斜狭缝阵列金膜的超强透射。

1 计算模型与理论

模拟结构如图1所示。双层金薄膜上均有周期性的同一倾斜狭缝，结构置于空气中。其大小设置为Lx×Ly=800 nm×200 nm，空间步长取Δx=Δy=1 nm，时间步长取Δt=Δx/2c（c为真空中光速）。采用宽频率范围高斯脉冲作为光源，y方向偏振的电磁波沿x方向正入射至结构。计算单元的上下边界用周期性边界条件，左右边界用完全匹配层条件。

金属纳米结构采用Drude模型，其介电常数为：

式中：ω为入射光频率；

ωP为表面等离子体频率；

γ为阻尼系数，与能量损失有关。

在Drude模型中，据参考文献[18]，金膜结构的参数分别为ωP=1.374×1016s-1，γ=4.08×1013。2层薄膜厚度均设为h=200 nm，晶格常数a0=200 nm，薄膜间距l=60 nm，a=50 nm和b=20 nm分别表示狭缝宽边和窄边的宽度，且均保持不变，d表示2层狭缝之间的侧向位移（狭缝相对位置），即2层薄膜狭缝中心的偏差距离。

对平板薄膜，由于其表面等离子体激元的色散曲线位于介质光锥外侧，因此金属-介质界面的表面等离子体是束缚态。金属-介质界面的电场为

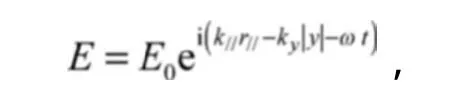
对于厚度为h的金属薄膜，表面等离子体色散将被改变，这是由于薄膜上下表面的表面等离子体激元会发生干涉，即

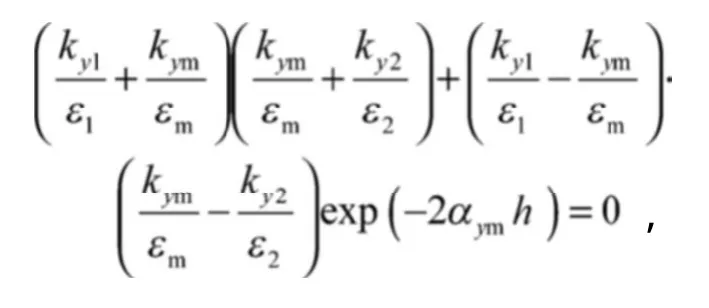
对于相对较厚的金属膜，金属两边的表面等离子体激元色散基本上是非耦合的。

2 结果与讨论

研究侧向位移d变化对金膜模拟结构的光学和等离子体激元性能的影响。图2给出了侧向位移不同时金膜结构随波长变化的归一化透射谱。图中谱线a～d对应的侧向位移分别为0,20,30,40 nm。

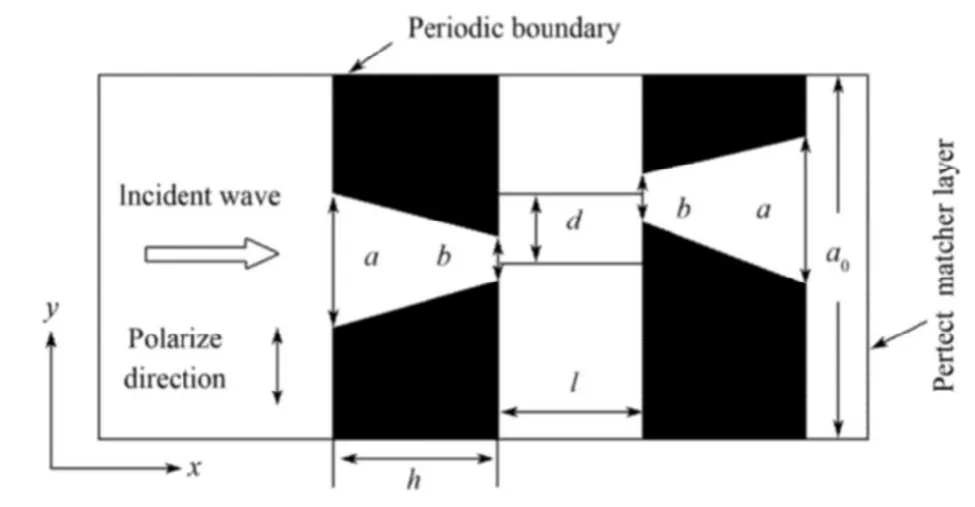
图1 双层金膜横截面结构图Fig.1xy cross sectional chart of 2-layermetallic film structure

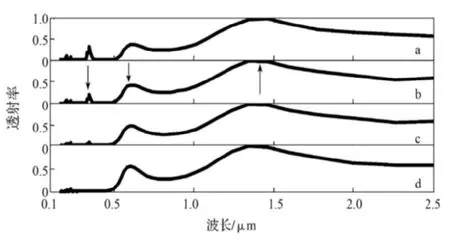
图2 金膜结构的归一化透射谱Fig.2Normalized transmission spectra of 2-layer metallic film structure

从图2可看出：1）透射谱图在波长200～500 nm均存在不同宽度的光学禁带。2）当侧向位移d增大时，位于0.348 8m处的共振透射峰强度降低，至d=40 nm时消失。而位于0.604 4m处的等离子体共振峰强度随侧向位移的增大略增强。对于1.341 μm处的共振峰而言，透射几乎达到100%，且峰强、峰的形状以及峰中心位置并不随d变化而改变。3）3个不同位置的共振峰宽度差别较大，低能（长波处）共振峰的峰宽总是大于高能（短波处）共振峰的峰宽。分析其激发机制为：当光入射至金属倾斜狭缝时，表面等离子体激元在狭缝边缘处被激发。2个短波处的共振峰是由表面等离子体共振（surface plasmon resonance，SPR）导致，而长波处的共振模式解释为局域波导共振，此时，金膜中的每个空气狭缝可以看做是一段两端向空气中开口的长方形波导，每个波导形成一个低品质因子的谐振腔，此谐振腔与狭缝形状关系密切，与狭缝排列方式关系不大，且无论薄膜厚度为多小，局域波导共振模都存在，这可以用Fabry-period效应解释[9]。

下面解释局域波导共振模透射率接近1的原因。当光入射在狭缝阵列上时，经历倏逝衰减，很少一部分光能够传输。但由于狭缝宽度远比光波波长要短，光波在狭缝中逐渐消逝，倏逝模照在狭缝上壁并被反射回来，然后又被下壁反射，其在狭缝内的如此多重反射作用形成了一个Fabry-Perot谐振腔模。虽然任一个镜面传输都很小，但如果入射光在出射之前在2镜面之间干涉加强，该Fabry-Perot谐振腔的净传输大小t会接近1。把腔内多重反射求和，则t可表示为式中：τ为2镜面间的透射系数；

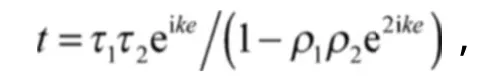
k为腔中光波波矢；

e为2镜面之间的光路长度。

表面等离子体共振和局域波导共振模式可通过FDTD模拟电场分布来进一步理解。图3给出了图2中谱线b箭头所指3个不同共振模式稳态时的瞬时电场分量Ex（图片a～c）和Ey（图片d～f）的空间分布情况。图中色柱表示场强强弱与颜色的对应关系，例如，色柱为0.2的颜色表示对应于图中这个颜色的场强相对强度较强，颜色越深，场强越大。对于SPR模式来说，图片a和b显示，Ex主要分布在倾斜狭缝的边缘和尖角处，但图片b显示第2层薄膜中的Ex强度明显比第1层弱得多。正负电场在狭缝间交替分布（以“+”和“-”标记），这种分布与沿y方向偏振的局域电偶极子振荡一致。这些偶极子与相反的表面电荷相互作用，结果在空气狭缝中形成一个驻波共振模式的切向电场Ey，如图片d和e所示。主要考察图片e可发现，Ey几乎全部局域在空气狭缝的两端开口处，且在狭缝入口处为正，在出口处为负，因此，将导致不同电负性的表面等离子体激元强烈耦合。Ey分别局域在狭缝的两侧，表明这种共振模式是由于结构的周期性所导致的。图片c和f表示局域波导共振模式电场分布。可发现Ex主要集中在狭缝的尖角处和2层薄膜之间，而在空气狭缝中间Ex分布较弱。Ey局域在狭缝中间，第1层狭缝中电场为负而第2层狭缝中电场为正，好像在2层薄膜之间出现一个波节。局域波导共振模式从第1层金膜经过2层金膜之间的空气隙到达第2层金膜，通过金膜的自导引行为传输。

图4 稳定态时总能量分布图Fig.4The total energy distribution at steady-state

图3 不同波长的电场分量空间分布图Fig.3The electric field component distribution at different wavelengths

3 结语

运用FDTD方法，研究了侧向位移对具有倾斜狭缝阵列的双层金膜光学透射及等离子体特性的影响。透射特征的物理起因归结于与孔的大小和形状有关的局域波导共振和与周期性有关的表面等离子体共振。对局域波导共振来说，每个空气纳米狭缝可看作一段两端开口的金属波导形成的低品质因子的共振腔，而表面等离子体共振是由结构的表面周期性决定的。这2种模式在增强透射现象中均起重要作用，通过详细分析相关电场和电磁场能量分布，更好地解释了光穿过狭缝的机制。

[1]Ebbesen T W, Lezec H J, Ghaemi H F, et al.Extraordinary Optical Transmission through Sub-Wavelength Hole Arrays[J].Nature, 1998, 391(12)：667-669.

[2]Chowdhury M H, Catchmark J M, Lakowicza J R.Imaging Three-Dimensional Light Propagation through Periodic Nanohole Arrays Using Scanning Aperture Microscopy[J].Appl.Phys.Lett., 2007, 91(10): 103118(3p).

[3]Stark P R H, Halleck A E, Larson D N.Short Order Nanohole Arrays in Metals for Highly Sensitive Probing of Local Indices of Refraction as the Basis for a Highly Multiplexed Biosensor Technology[J].Methods, 2005, 37 (1)：37-47.

[4]Fang N, Lee H, Sun C, et al.Sub-Diffraction-Limited Optical Imaging with a Silver Superlens[J].Science, 2005, 308 (5721) ：534-537.

[5]Martin-Moreno L, Garcia-Vidal F J, Lezec H J, et al.Theory of Extraordinary Optical Transmission through Subwavelength Hole Arrays[J].Phys.Rev.Lett., 2001, 86(2) ：1114-1117.

[6]Garca-Vidal F J, Lezec H J, Ebbesen T W, et al.Multiple Paths to Enhance Optical Transmission through a Single Subwavelength Slit[J].Phys.Rev.Lett., 2003, 90(21):213901(4p).

[7]Tang Z H, Peng R W, Wang Z, et al.Coupling of Surface Plasmons in Nanostructured Metal/Dielectric Multilayers with Subwavelength Hole Arrays[J].Phys.Rev.B, 2007,76 (19): 195405(8p).

[8]Ruan Z, Qiu M.Enhanced Transmission through Periodic Arrays of Subwavlength Holes: The Role of Localized Waveguide Resonance[J].Phys.Rev.Lett., 2006, 96(23):233901(4p).

[9]Garcia-Vidal F J, Moreno E, Porto J A, et al.Transmission of Light Through a Single Rectangular Hole[J].Phys.Rev.Lett.,2005, 95(10): 103901(4p).

[10]Przybilla F, Degiron A, Laluet J Y, et al.Optical Transmissionin Perforated Noble and Transition Metal Films[J].Journal of Optics A: Pure and Applied Optics, 2006, 8(5) ：458-463.

[11]Sun Mei, Tian Jie, Li Zhiyuan, et al.The Role of Periodicity in Enhanced Transmission through Subwavelength Hole Arrays[J].Chinese Physics Letters, 2006, 23(2) ：486-488.

[12]Przybilla F, Genet C, Ebbesen T W.Enhanced Transmission through Penrose Subwavelength Hole Arrays[J].Applied Physics Letters.2006, 89(12): 121115(3p).

[13]Lezec Henri J, Thio Tineke .Nanophotonics[J].Optics and Photonics News, 2004, 15(12): 29.

[14]Zhai Xiang, Liu Jianqiang, He Mengdong, et al.Adjustable Phase Resonances in a Compound Metallic Grating with Perpendicular Cuts[J].Optics Express, 2010, 18(7) ：6871-6876.

[15]Liu Zhimin, Li Hongjian, Xie Suxia , et al.Tunable Phase Resonances in a Compound Metallic Grating with Perpendicular Bumps and Cuts[J].Optics Express, 2011,19(5) ：4217-4222.

[16]Li Hongjian, Xie Suxia, Zhou Renlong, et al.Two Different Transmission Tunnels of Light Through Double-Layer Gold Nanohole Arrays[J].Journal of Physics: Condensed Matter,2008, 20(41): 415223(6p).

[17]Cheng Chen, Chen Jing, Shi Dajian, et al.Physical Mechanism of Extraordinary Electromagnetic Transmission in Dual-Metallic Grating Structures[J].Phys.Rev.B, 2008, 78(7):075406(9p).

[18]Palik Edward D，Ghosh Gorachand .Handbook of Optical Constants in Solids：Volume 3[M].Boston: Academic Press, 1998: 12-13.