三维轴对称驻点流系统的一些研究

张明捷, 党龙飞, 徐艳芝

(成都信息工程学院数学学院,四川成都610225)

1 Introduction

In this paper,we are concerned with the following third order differential equations arising in the boundary layer theory

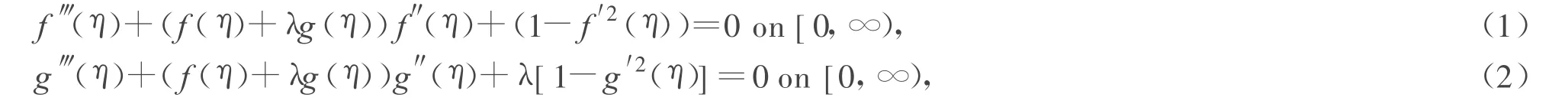
with boundary conditions

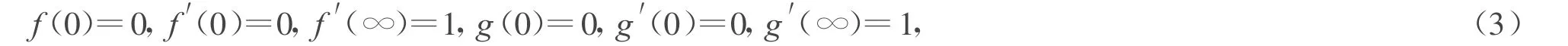
Which has been used to describe the 3D axisymmetric inviscid stagnation flow[1,2].A solution of(1)～(3)is called a similarity solution.The two-dimensional case,λ=g=0,was solved by Hiemenz[3].The axisymmetric stagnation flow towards a plate,λ=1 and g=f,was solved by Homann[4].Howarth[5]studied the case 0＜λ＜1 which can be applied to the stagnation region of an ellipsoid.Davey[6]investigated the stagnation region near a saddle point(-1＜λ＜0).For λ≤-1 the vorticity generated is not confined in the boundary layer and the existence of solutions cannot be shown[2].Up to now,there is a little study on the case of λ≤-1.

Utilizing the integral methods[7,8],Du Hauang and Zhang[9]presented a system of two integral equations on the case of λ＜0 and obtained some properties and a non-existence result of(1)～ (3)on the case of λ＜-4.

In this paper,we shall study(1)～ (3)for the case of λ∈ R and λ≠0,we shall obtain further results on(1)～(3)and a new non-existence result on the case of λ≤-1.

2 Positive solutions of a system of two integral equations

In[9],Du,Hauang,Zhang presented a system of two integral equations

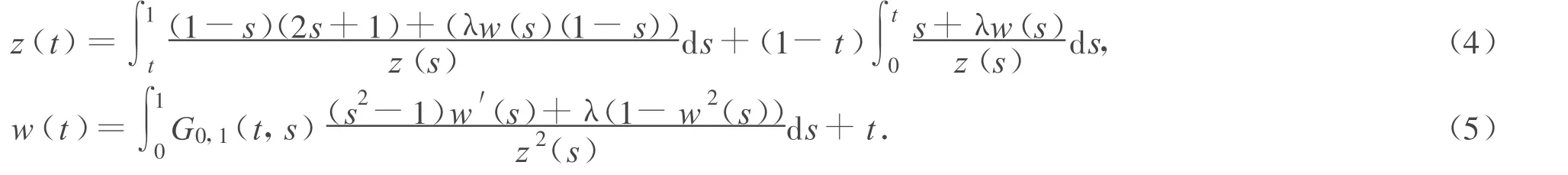
Where G0,1(t,s)denotes the Green function for u″(t)=0 with u(0)=0 and u(1)=0 defined by

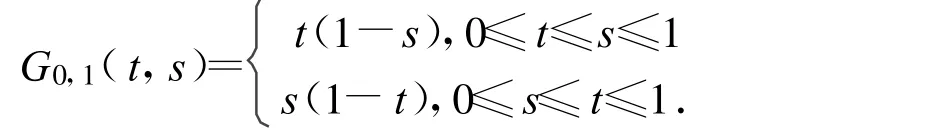
They obtained the following results：

(i)For λ＜0(1)～(3)has a solution in∑if and only if(4)～(5)has a positive solution

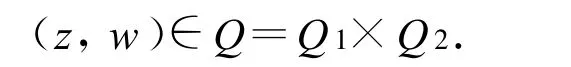
(ii)For λ＜-4(1)～(3)has no solution in ∑.

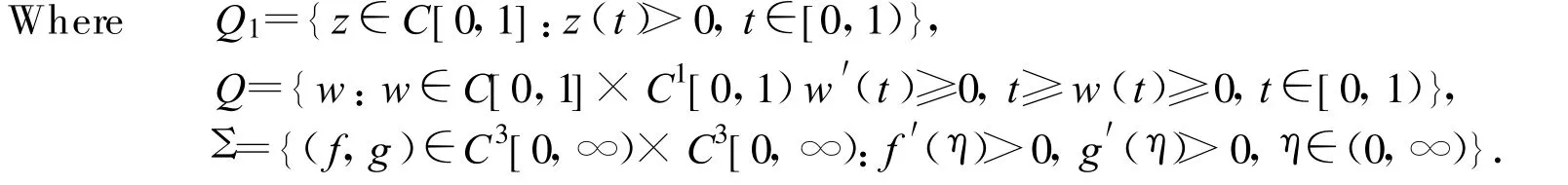
In this paper,let

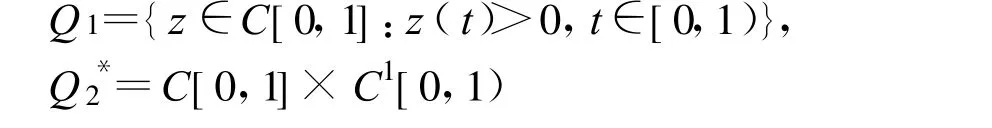
and

Theorem1 If(λ,z,w)∈(-∞,+∞)×Q is a solution of(4)～(5),then

(iii)w(0)=0,w(1)=1 and w(t)≥-1 for t∈[0,1]if λ＜0 and w(t)≤1 for t∈[0,1]if λ＞0.

(i)Firstly,we prove z(t)=0.

If z(1)≠0,then z(t)≠0,t∈[0,1].

By the continuity of z(t),then m=min{z(t),t∈[0,1]}＞0.From this and λ＞0,we obtain by(4)

This implies

a contradiction.Hence,(i)holds.

Since z(t)＞0 for t∈(0,1),we have

Integrating this inequality from 0 to ξ,we have

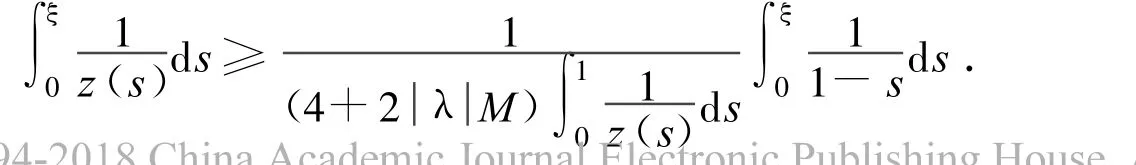
From this we obtain

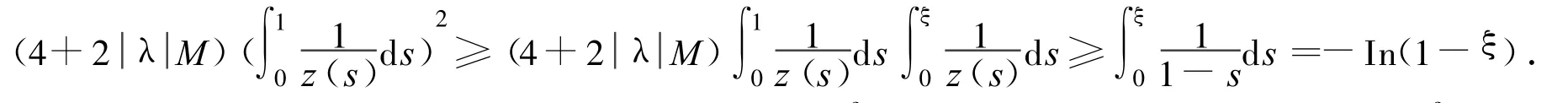
Letting ξ→1-in the last inequality,we have,which contradicts∞.Thus,(ii)holds.

(iii)Letting t=0 and t=1 in(5),we have w(0)=0 and w(1)=1.

If λ＞0 and there exist t0∈[0,1]such that w(t0)＞1.Since w(0)=0,and w(1)=1,there must be exist t*∈(0,1)such that w(t*)=max{w(t)：t∈[0,1]}and w(t*)＞1.

By(5),we have

Reamrk1 Since we do not assume λ＜0 and Q ⊆Q*,hence Theorem 1 in[9]is improved.

Utilizing the solutions of(z,w)∈Q*,we may construct the solutions of(1)～(3)and then the use of(4)～(5)is expanded.

Theorem2 If(z,w)∈Q*is a solution of(4)～(5),then(1)～(3)has a solution(f,g).

Proof.Let(z,w)∈Q*be a solution of(4)～(5).By Theorem 1(ii),we have

Let

Then η(t)is strictly increasing on[0,1)and

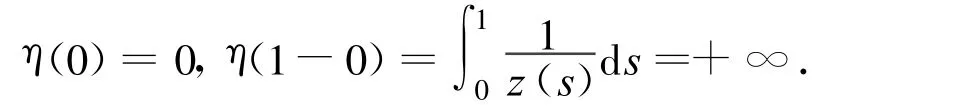
Let t=h(η)be the inverse function to η=η(t),we define the function

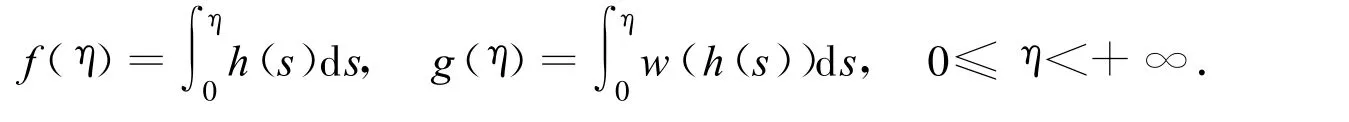
Then

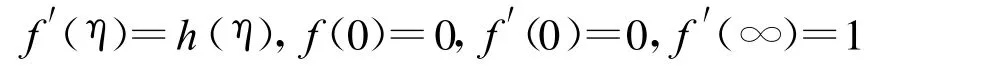
and

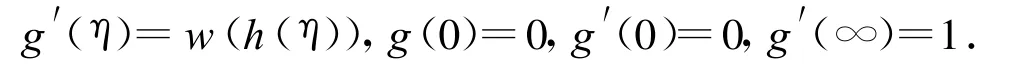
From(6),we have

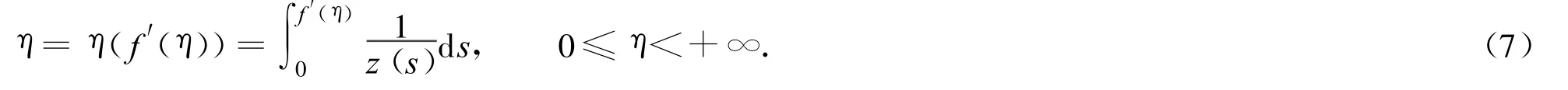
Differentiating(7)with respect to η,we have

Then f″(η)＞0 for 0≤η＜+∞.

Differentiating(8)with respect to η,we have

Differentiating(4)with respect to t,we have

By setting s=f′(α)and utilizing t=f′(η)and(8),we have

By(8)～(11),we have

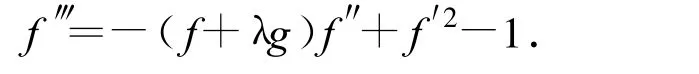
Combing(10)and(11),we obtain

This completes the proof.

3 A non-existence result on(1)～(3)

Let

Lemma1 Let λ＜0.If(f,g)∈Γis a solution of(1)～(3),then g″(∞)=0.

Proof.Since g′(+∞)=1,we have

Since(1)～(3),we have g‴(0)=-λ,and λ＜0.then g‴(0)＞0 and g″(η)＞0.we have ∃η*,such that g″(η)is increasing on[0,η*].(12)implies that there exists η0∈[η*,+∞)such that g″(η0)＜g″(η*).Then we prove that g″(η)is decreasing on(η0,+∞).If there must exist η1,η2∈[ η0,+∞)with η1＜η2such that g″(η1)＜g″(η2).So let ˜η∈[ η*,η2]such that g″(˜η)=min{g″(η)：η∈[ η*,η2]}.This implies g‴(˜η)=0 and g(4)(˜η)≥0.

Differentiating(2)with η,we have

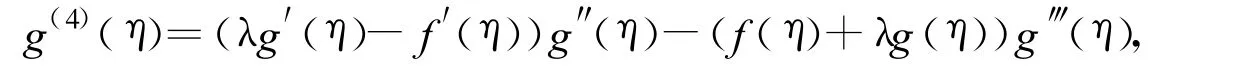
then

By(f,g)∈Γand λ＜0,we have g(4)(˜η)≤0,a contradiction.Hence g″(η)is decreasing on[ η0,+∞)and thenexists.By(12),we obtain g″(∞)=0.

Theorem3 If λ≤-1,then(1)～ (3)has no solution in Γ.

Proof.The proof is by a contradiction.If(1)～ (3)has a solution(f,g)in Γ,then g″＞0.

Let η：=η(t)=(g′)-1(t)for t∈[0,1)be the inverse function to t=g′(η)：[0,∞)→[0,1).It follows that g′is strictly increasing with[0,+∞)and η(t)=(g′)-1(t)：[0,1)→[0,∞)with(g′)-1(0)=0

Let x(t)=g″(η)＞0 for t∈[0,1),by Lemma 1,x(1)=.This implies that x(t)＞0 for t∈[0,1)and x is continuous on[0,1).By Lemma 1,we see that x is continuous from the left at 1.Hence,we have x(t)∈C[0,1]and x(1)=0.

Using the Chain Rule to x(t)=g″(η),we obtainand by the Inverse Function Theorem,we have

This,together with g′(η)=t,implies

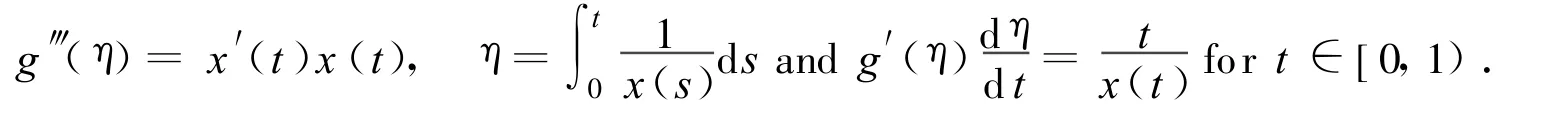
Integrating the last equality from 0 to t implies

Let y(t)=f′(η)for t∈[0,1),y(1)=1,then y(t)∈ C[0,1)and 0≤y(t)≤1.Notice thatwe have

Substituting g,g′,g″,g‴and f into(2)implies

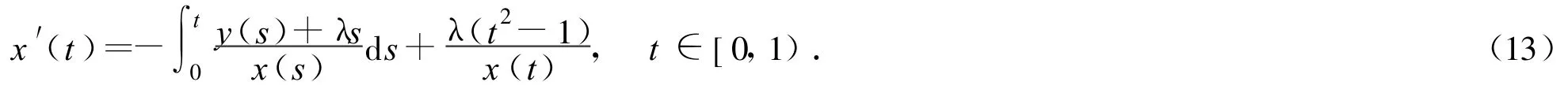
Integrating(13)from t to 1,we have

By x(1)=0,then

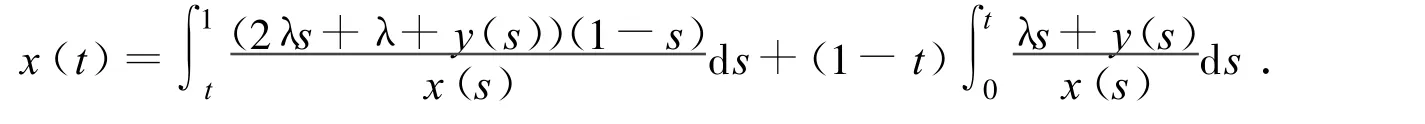
we have

Reamrk2 Theorem 12 improves non-existence result of(1)～ (3)in[6]from λ＜-1 to λ≤-1.

[1]C Y Wang.Axisymmetric stagnation flow on a cylinder[J].Quart.Appl.Math.1974,32：207-213.

[2]C Y Wang.Similarity stagnation point solutions of the Navier-Stokes equations-review and extension[J].European Journal of Mechanics B/Fluids,2008,27：678-683.

[3]K Hiemenz.Die Grenzschicht an einem in den gleichformingen Flussigkeitsstrom eingetauchten graden Kreiszylinder[J].Dinglers Polytech.J,1911,326：321-324.

[4]F Homann.Der Einfluss grosser Zahigkeit bei der Stromung um den Zylinder und um die Kugel[J].Z.Angew.Math.Mech.,1936,16：153-164.

[5]L Howarth.The boundary layer in three dimensional flow-Part∏.The flow near a stagnation point,Philos[J].Mag.Ser.,1951,742：1433-1440.

[6]A Davey.A boundary layer flow at a saddle point of attachment[J].J.Fluid.Mech.,1961,10：593-610.

[7]G C Yang.Existence of solutions of laminar boundary layer equations with decelerating external flows[J].Nonlinear Analysis,2010,72：2063-2075.

[8]K Q Lan,G C Yang.Positive solutions of the Falker-Skan equation arising in boundary layer theory[J].Canad.Math.Bull.,2008,51(3)：386-398.

[9]C Du,S J Huang,M J Zhang.On 3D axisymmetric inviscid stagnation flow related to Navier-Stokes equations[J].Nonlinear Analysis Form,2011,16：67-75.