目标跟踪中参考模型的自动初始化方法

程明智, 高俊祥

(1.北京印刷学院,北京102600;2.华中农业大学理学院,湖北武汉430070)

1 引言

目标跟踪是视频会议、远程教育、和智能监控等系统的重要组成部分,在现有主要跟踪算法中,必须首先在参考帧中定义一个参考模型,然后在后续帧中比较候选目标和参考模型的相似性来确定目标的位置[1]。目前,参考模型的初始化一般是手动进行的,开始跟踪前在参考帧中手动画一个包含目标的矩形或椭圆并将内部的像素集作为参考模型[2]。虽然有少量文献采用了自动初始化,但是一般需要目标的先验知识,因而限制了算法的通用性。例如,文献[3]提出的方法由于采用了肤色信息因而仅适用于人脸的跟踪。文献[4]的投影法具有计算简单的优点,但是若场景中多个目标的投影有重叠的部分,则可能会出现无法确定目标数量、位置或尺度的情况。

针对目标跟踪中参考模型的初始化需要手动完成以及投影法的缺陷,提出了一种自动、精确初始化参考模型的方法,参考模型为二维空间内的一个椭圆。首先采用连通组分标记算法对目标进行计数,并计算每个目标的位置;然后根据回转半径张量法求出包含目标的最小外接矩形;最后从最小外接矩形的参数出发用蒙特卡洛算法求出参考模型的估计,估计过程以统计学中的F指标最大为准则。

2 投影法的缺陷分析及应对策略

投影法首先根据图像的垂直投影(即投射到横坐标轴上的投影)确定目标的水平位置、宽度和数目;然后再对图像进行水平投影(即投射到纵坐标轴上的投影)获得目标的垂直位置和高度。下面分析投影法初始化参考模型的问题并提出对应策略。

第一,如果场景中的目标不只一个而且目标的投影有重叠的部分,则有可能造成目标的数量、位置或尺度的模糊性,即目标的个数、位置或尺度不能从投影信息准确获得。第二,投影法算出的参考模型是目标的竖直外接矩形,如果目标在图像中是倾斜状态时,参考模型内将会包含大量不属于目标的像素。第三,如果目标的紧凑性较低会使大量背景像素进入参考模型,从而降低参考模型对目标的描述能力。

应对策略如下。第一,目标的投影重叠引起的模糊性是投影法的固有缺陷,因而本文摈弃了这种检测目标数目和位置的方法,采用连通组分标记算法对目标进行计数,并计算每个目标的位置,从根本上避免了投影重叠带来的问题。第二,能够包含所有目标像素但同时非目标像素又最少的矩形是最小外接矩形而非竖直外接矩形,因而算法采用了前者。最小外接矩形的面积一般小于竖直外接矩形,从而包含的非目标像素更少。第三,当目标的结构比较松散时外接矩形会很大,根据F指标统计最大化的原则舍弃了少量目标像素,同时能够把更多的背景像素排除在模板之外。

3 参考模型的自动初始化算法

3.1 连通组分标记算法

在跟踪前目标检测步骤已经完成,令目标检测获得的运动目标掩码是二值图像 M(x,y),如果存在一个像素集M(xi,yi)=v(i=0,1,2,…,n),其中 v=0或v=1,并且对序列中任何两个像素都可以通过v值相连接,则称这个像素集合是一个值为v的连通组分。如图1(a)是一幅二值图像,内有值为1的5个连通组分。对二值图像M(x,y)做标记,生成标号图LB,标号图像中每个像素的值就是像素所在连通组分的标号,标号是一个是用于标记连通组分的整数,图1(b)显示的是对图1(a)的的标记结果。其详细计算过程可参照相关文献[5]。

图1 内含5个值为1的连通组分的二值图像

3.2 目标的最小外接矩形

图像中的目标不一定是竖直的,处于倾斜状态的目标直接求其最小外接矩形是比较困难的,首先将目标旋转一定角度使其扭正,而旋转矩阵采用回转半径张量法求取,旋转之后目标竖直外接矩形和最小外接矩形是重合的,因而矩形的位置和尺度容易求出。

令包含一个目标的连通组分标号图像为LBk(k=1,2,…,K),对运动目标的 n个像素点的坐标求均值得到目标的中心坐标(m,c),各像素的坐标分别减去中心坐标后得到各点相对坐标(u,v),则用相对坐标值(u,v)可以组成n×2维矩阵X：

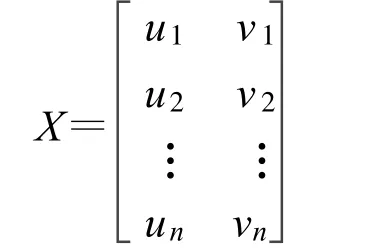
求矩阵X的内积,令 V=XTX/n,其中回转半径张量V是2×2矩阵,它的两个特征向量构成矩阵U,设旋转矩阵为 R,则

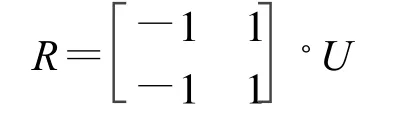
旋转矩阵R求出后,可用其对所有目标像素进行旋转。令旋转后各像素的坐标为(xi,yi),则旋转方程可表示为

此时目标在图像中已经处于竖直状态且每个连通组分标号图像LBk中只有一个目标,用前面讲述的投影法即可确定最小外接矩形的宽 W和高H。在二维空间中,旋转可以用一个角度 α定义,逆时针旋转α取正,反之取负。一个列向量关于原点旋转α角的矩阵是：

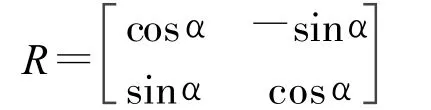
可推出

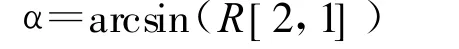
于是可以用一个五维向量(m,c,W,H,-α)T表示图像LBk中目标的最小外接矩形,其中(m,c)表示矩形的中心,(W,H)表示矩形的宽和高,-α表示矩形的倾斜角度。

3.3 蒙特卡洛算法计算椭圆参考模型

目前衡量一个参考模型的准确性还没有一个公认的标准,借鉴统计学中F指标的思想定义一个准确性度量参数：

式中

式中,TP代表属于参考模型同时又属于目标的像素数量;FN代表不属于参考模型但是属于目标的像素数量;FP代表属于参考模型但是不属于目标的像素数量。F取值在[0,1],并且F值越大说明参考模型越准确。

算法的目的是计算出用椭圆表示的参考模型,令该椭圆用向量 S=(x,y,Hx,Hy,θ)表示,其中(x,y)代表椭圆中心,(Hx,Hy)代表半轴长度,θ为椭圆的倾斜角度,从而参考模型就是能够使F取得最大值的椭圆。从理论上说可以用遍历法在最小外接矩形附近搜索,但是由于需要在每一维上搜索因而计算量过大。采用蒙特卡洛模拟的思路对向量S进行估计：对S采样得到N个样本Si(i=0,1,2,…,N),并根据F指标赋予各个样本权值wi,权值总合为1,而向量S的估计为：

蒙特卡洛模拟的原理可参照相关文献[6],Si和wi按下述过程计算。一个合理的假设是椭圆中心(x,y)在最小外接矩形中心(m,c)的邻域内,而半轴长度(Hx,Hy)和最小外接矩形的宽、高(W,H)的一半相近,椭圆的倾斜角度θ也与最小外接矩形的倾角-α相似。因而Si为

其中vi是零均值高斯白噪声序列,对于每一个样本Si,都可以计算出一个指标Fi,因而权值wi为：

式中 σ为Fi的标准差。在样本 Si和权值wi获得以后,代入即可计算出参考模型S。

4 实验结果

采用算法对多条视频序列进行了参考模型的初始化,下面以其中的5条序列为例进行分析。为方便起见将它们重新命名为S1～S5,序列中的运动目标包括人、车辆和圆形的球,它们具有不同的形状、个数、颜色和运动状态,详细信息列于表1中,算法在Matlab7.0环境下实现。

表1 实验序列详细信息

用文中算法与手动初始化方法、投影法相比较,为了使比较更公平投影法中的目标模板采用竖直外接矩形的内接椭圆。图2至图6展示了比较结果,每幅图从左向右依次是手动、投影法和文中算法的处理结果。从S1的处理结果来看,图2(c)包含了绝大部分目标像素但是脚部排除在椭圆之外,这是由于图中目标的中心与目标外接矩形的中心并不重合而是处在偏右的位置,因而最左端的脚部没有包含在椭圆中。虽然与图2(c)相比图2(b)中的目标几乎没有遗漏,但是椭圆尺度的扩大使得大量背景像素进入到参考模型中,这显然是得不偿失的。在S2的处理结果图3(c)中,椭圆将两辆汽车完整地包含在参考模型中,同时其中只有极少数背景像素。图3(b)中的非目标像素则要多一些,如图中的黑色箭头所示;另外则有部分本应属于目标的像素排除在了参考模型之外,如图中的白色箭头所示。

图3 序列S2用3种方法初始化参考模型的结果

序列S1和S2的处理结果虽然有些差异,但总体上来说并不显著,所有参考模型均能比较准确地反映目标的特性,序列S3、S4和S5则能更明显地体现出文中算法的优越性。序列S3中的目标在图像中处于倾斜状态,这种情况使得图4(b)中大量的背景像素进入椭圆而运动目标的头部和脚部却排除在椭圆之外;图4(c)中并没有出现这种情况,这是由于图中的椭圆在平面内进行了旋转因而适应了目标的倾斜状态。图5中的垂直投影能够准确区分出三个圆球,但是水平方向的投影有一部分发生重叠,在投影法中水平投影对应着目标的高度,因而图5(b)中目标高度明显增加。图中的三个目标虽然投影重叠,但是目标本身并没有遮挡因而将它们分割成各自独立的目标没有任何困难,所以在图5(c)中算法可以不受投影重叠的影响精确地计算出参考模型。在图6中,图像中的两个人不但水平投影是重叠的,而且垂直投影也发生了重叠,其结果是投影法会将两个目标判断为一个目标导致建立参考模型失败。与序列S4的情况类似,图6(c)中采用算法可以不受投影重叠的影响。

图4 序列S3用3种方法初始化参考模型的结果

图5 序列S4用3种方法初始化参考模型的结果

图6 序列S5用3种方法初始化参考模型的结果

5 结束语

提出了一种自动、精确初始化参考模型的方法。采用文中算法对不同性质的视频序列进行了广泛的实验,结果表明在不同的场景下算法均能准确完成参考模型的初始化,计算出的模型能够体现目标的视觉特征,从而为参考模型的初始化提供了一种有效的方法。

致谢：中央高校基本科研业务费专项资金资助项目(2010BA016);北京印刷学院本科生科学研究计划资助项目(08150111007)对本文的资助。

[1]Leven W F,LantermanA D.Unscented Kalman Filters for Multiple Target Tracking with Symmetric Measurement Equations[J].IEEE Transactions on Automatic Control,2009,54(2)：370-375.

[2]Kyriakides I,Morrell D,Papandreou-Suppappola A.Sequential Monte Carlo Methods for Tracking Multiple Targets with Deterministic and Stochastic Constraints[J].Signal Processing.2008,56(3)：937-948.

[3]Pernkopf F.Tracking of Multiple Targets Using Online Learning for Reference Model Adaptation[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B：Cybernetics.2008,38(6)：1465-1475.

[4]Wang J T.Research on Object Detection,Tracking and Behavior Recognition in Video Sequences[D].Nanjing University of Science and Technology,2008.

[5]Shapiro L G,Stockman G C.Computer Vision[M].Prentice-Hall,2001.

[6]Mendo L,Hernando J M.Improved Sequential Stopping Rule for Monte Carlo Simulation[J].IEEE Transactions on Communications.2008,56(11)：1761-1764.