基于ANSYS 的岩质边坡软弱结构面非线性接触分析
2011-06-27苏向震,张程宏,李锐
苏 向 震, 张 程 宏, 李 锐
(1.中国市政工程西南设计研究总院,四川成都 610081;2.长江岩土工程总公司,湖北武汉 430010)
1 引言
在岩质边坡中存在各种形式的软弱结构面,如裂隙、断层、软弱夹层等。岩质边坡的稳定性往往受控于软弱结构面的变形和受力特征,因此,软弱结构面成为岩质边坡稳定性分析的热点。目前,处理软弱结构面问题的有限元方法主要有两种,即连续体法和接触单元法。连续体法实质上是强度问题,其优点是方法简单、力量成熟、计算耗时短,但是其不能很好的模拟软弱结构面的张开和滑移特征,精度不高;接触单元法是用界面的正应力和剪应力以及界面位移约束来描述界面的粘结开合状态,其特点是接触界面的区域大小和相互位置以及接触状态事先未知,随时间变化需要在求解过程中确定,且接触条件属单边性,表现出强烈的非线性,能够很好的模拟结构面的变形和受力特性。
笔者采用增广拉格朗日算法,借助有限元分析软件ANSYS,建立了某岩质边坡软弱结构面接触模型,考虑到软弱结构面的工作性态对边坡稳定的影响,利用非线性有限元技术为边坡稳定性分析提供参考。
2 接触分析的基本理论
接触问题是一种高度的非线性问题,主要包括以下三种非线性:接触边界条件的非线性,即接触区的范围一般事先未知,并在接触过程中可能还会变化;材料非线性,表现在应力集中产生的局部塑性变形;几何非线性,在应力集中情况下往往产生局部大变形。因此,对未知接触面和接触作用力以及接触体之间摩擦力的模拟,无论从数学理论上,还是计算实施中都比经典线性结构力学问题复杂。
求解接触问题的数值方法主要有Lagrange法、罚函数法以及增广Lagrange法。将接触边界条件用Lagrange乘子相乘,并与总势能一起构成修正的势能,再求驻值以得到最后的控制方程,该方法即为Lagrange法。Lagrange法可以很精确的满足约束条件。但由于Lagrange乘子的引入,增加了自由度,系统的求解规模增大了,而且在系统的控制方程中出现了零主元,给计算带来了麻烦。罚函数法是求解接触问题的典型方法之一,它将接触区域的非嵌入条件以及其他条件作为惩罚项引进接触系统的能量泛函中,使原来的条件约束变分问题转化为罚优化问题,实际上就是将接触非线性问题转化为材料非线性问题。罚函数法的最大优点在于引入接触条件时并不增加系统的自由度,而且很容易从物理意义上解释。缺点在于罚函数往往导致方程病态,随着罚值增加,病态减弱,而约束条件只有在罚值很大时才能精确满足。由于Lagrange法和罚函数法各有优缺点,于是将两者联合使用,产生了增广Lagrange法,通过一个罚函数强迫满足一个特定的关键约束。增广Lagrange法已成功应用于不可压缩弹性有限变形、无摩擦接触问题及弹塑粘性问题中。
设两个接触物体的张开函数为gN,初始张开为g0≥0,其接触条件为:
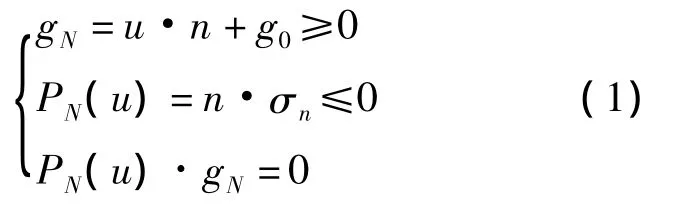
式中 u为接触边界的位移向量;n为接触边界的法向应力;σ为接触体的应力;pN(u)为接触边界的法向应力。由coulomb摩擦定律及kuhntucker条件:
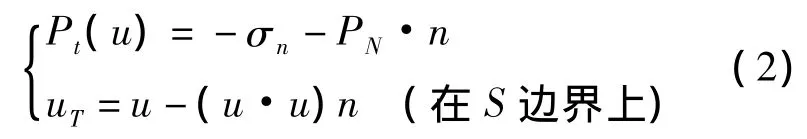
可以得到弱形式虚功方程:
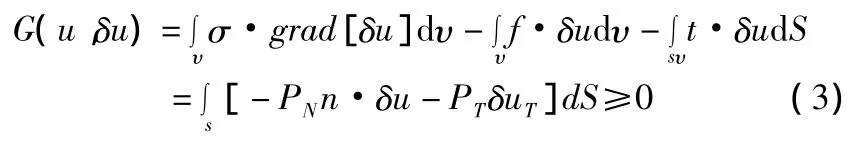
在 S边界上,如果 gn=0,则 δu·n≤0。
式中, PT(u)为接触边界的切向应力;uT为位移向量的切向分量;f,t分别为施加于接触体上的体力和面力;υ,S,S0则分别表示积分域是整个接触体、接触面及面力作用边界。
由于式(3)中的约束难以处理和求解,于是引入独立的Lagrange乘子λN,λT和罚规划,则式(3)可表示为:

式中 ξ为罚因子;Ф=‖λT‖-μλN,μ为摩擦系数;△N,△T为罚参数。
式(4)即为摩擦接触问题的增广Lagrange方程。
3 软弱结构面——岩石相互作用非线性分析
相互作用问题存在两种非线性:一是由于材料非弹性引起的材料非线性;一种是由于介质之间产生的局部滑移、脱离而造成的状态非线性。
(1)软弱结构面材料的模拟。
ANSYS提供了一种以Drucker-Prager准则为屈服准则的材料,屈服面不随材料的逐渐屈服而改变,即没有强化准则;塑性行为假定为理想弹塑性,采用相关联流动法则。文中所述的软弱结构面材料模型采用DP材料,为确定破坏面,共需输入3个参数,即粘聚力C,内摩擦角φ,膨胀角φf。为保守起见,文中取φf=0。
(2)软弱结构面与岩石接触面上的状态非线性模拟。
大多数情况下,岩质边坡的失稳破坏主要表现为结构面切割形成的岩块沿软弱结构面的滑移,岩块与基岩内部应力基本上处于弹性和弹塑性状态,因此,边坡块体稳定问题主要反映在软弱结构面上。一般而言,软弱结构面在承受一定外荷的情况下就有可能逐步发展成为滑动面。在边坡非线性稳定分析中,对滑动面的模拟即为状态非线性模拟。文中利用ANSYS程序的接触单元实现接触分析。软弱结构面作为接触面,岩石表面刚度相对要大一些,将其作为目标面,在软弱结构面表面形成接触单元,在岩石表面上形成目标单元,通过相同的实常数将相对应的接触单元和目标单元定义为一个接触对,通过选择合理的参数,实现软弱结构面与岩石界面上的粘结、滑移、张开、再闭合状态的模拟。
4 算例分析
4.1 计算模型
某岩质边坡坡高H=25 m,边坡浅表层为强风化Ⅳ类岩体,深部为弱风化Ⅲ类岩体,浅表层岩体中发育有两组结构面,结构面摩擦系数为0.4,边坡截面示意图见图1,有限元计算模型如图2所示,各岩层的计算参数如表1所示。
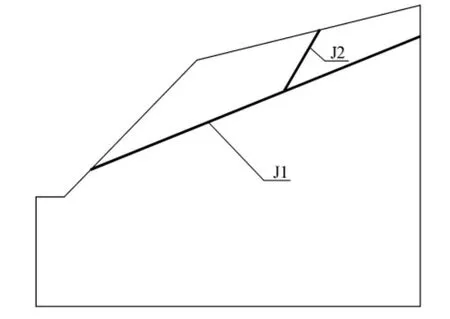
图1 边坡截面示意图

图2 有限元计算模型示意图
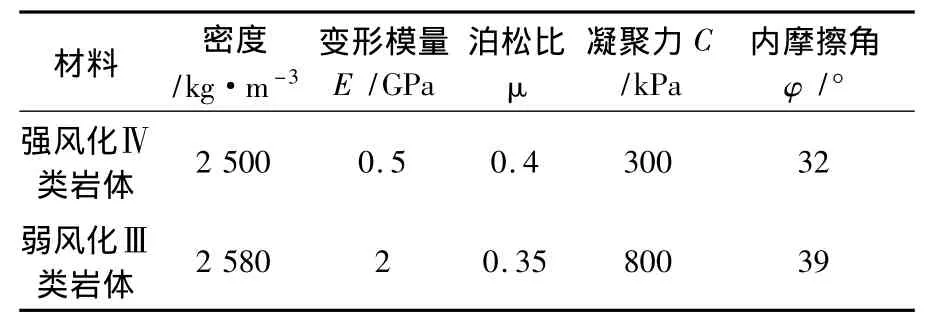
表1 计算参数表
4.2 计算结果分析
(1)边坡应力状态及特征
边坡大、小主应力等值线图及主应力矢量图见图3、4和5。从图中可以看出,在自重作用下,受斜坡地形、岩体质量类别以及断层岩脉软弱结构面的影响,边坡天然应力场呈现明显的分区、分带特征,即浅表地层的低应力带、中部的应力过渡区、深部岩体的应力平稳区以及断层岩脉附近的低应力条带。坡体大主应力等值线与坡面近于平行,且随水平和垂直埋深的增大,量值呈现增大的趋势;小主应力基本呈现顺坡分布的特点,且随埋深的增大而增大;同时,无论σ1还是σ3,由于受断层的影响,在覆盖层、断层及岩脉附近的等值线均不平稳,即出现一定的拉应力区域,拉应力最大值约 0.14 MPa。

图3 大主应力等值线图(单位:Pa)
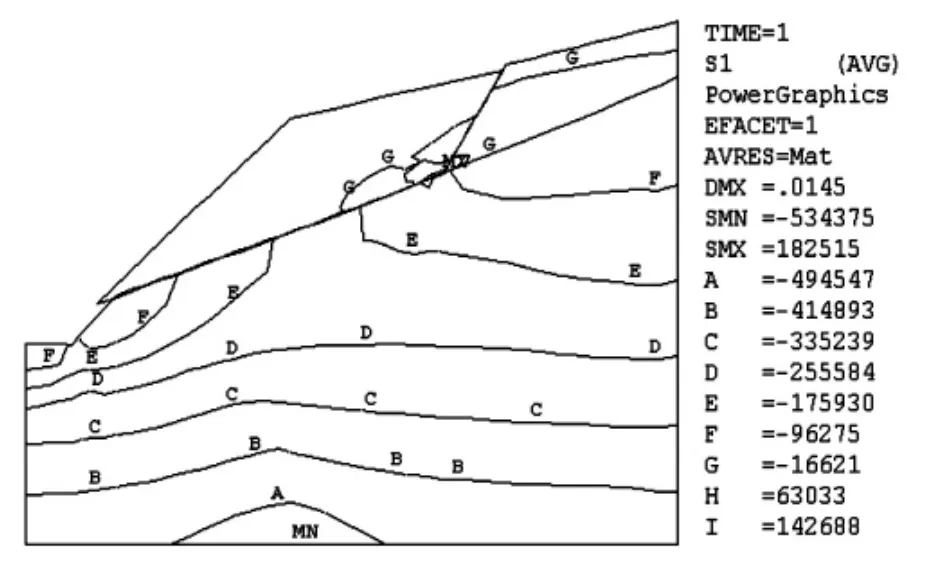
图4 小主应力等值线图(单位:Pa)

图5 主应力矢量图
(2)软弱结构面物理力学特征。
边坡在软弱结构面上存在的滑动趋势使得作为接触面的结构面上产生摩擦应力,如图6所示。从图6中可以看出,两条软弱结构面交汇处的摩擦应力较大,破碎带坡肩处摩擦应力几乎为0,坡肩部位处于变形拉裂区,软弱结构面上的有效应力减小,故摩擦应力较小。

图6 软弱结构面摩擦应力图(单位:Pa)
软弱结构面上的接触压力如图7所示,接触压力分布图与摩擦应力分布图相似。一般接触压力为0的位置,摩擦应力也为0,坡肩部位接触压力亦为0,说明该部位岩体有脱离母岩滑动的趋势,需对其进行加固处理。

图7 软弱结构面接触压力图(单位:N)
5 结语
笔者采用增广拉搁朗日算法,运用ANSYS有限元分析软件及其自带的接触单元模拟岩质边坡软弱结构面的粘结、滑移及受力特性,通过对接触部位的状态和应力进行研究,得出了接触部位的应力分布规律,合理反映出基岩与软弱结构面之间相互作用过程中的变形协调和应力传递关系,为边坡稳定性分析提供了可靠的依据。
[1]孙林松,王德信,谢能刚.接触问题有限元分析方法综述[J].水利水电科技进展,2001,21(3):18-20.
[2]许有飞,何江达,梁照江.混合式闸墙与基岩间的非线性接触分析[J].红水河,2004,23(4):71-75.
