直流牵引供电系统短路稳态电流的计算

龚廷志 吴命利

(1.六安供电公司，安徽 237006;2.北京交通大学 电气工程学院，北京 100044)

0 引言

直流牵引供电系统为运行的电力机车提供可靠的电能，它主要由降压变压器、整流器、馈电线、接触线(轨)、走行轨、回流线等组成。直流牵引供电系统的短路电流计算，是变电所设备选择、保护设计、判断变电所运行的安全可靠性，确定运行方式的重要依据。

近些年来，国内不少单位开展了直流牵引供电系统短路计算的研究［1-5］。文献［1，2］介绍了6脉波整流机组的3段线性化曲线模型，并探讨了短路稳态电流的计算方法，由于用3段线性化处理时，各等效区间的电流曲线不平滑，容易突变，这样就存在很大的误差。文献［3］介绍了24脉波整流机组的5段线性化曲线模型，并编写SimSystem软件，用于计算大型直流牵引网络的短路电流。文献［4，5］给出了直流牵引网短路试验的几个具体实例。本文对直流牵引供电系统原理图进行了简化，并结合24脉波整流机组的5段线性化曲线模型，编写了直流牵引网短路电流稳态值计算的程序和界面，并对上海地铁3号线和北京地铁6号线牵引网发生短路的情况进行仿真。

1 整流机组的外特性模型

在工程计算中，24脉波整流电路通常认为是由2个12脉波整流并列而成。对于12脉波整流电路，电抗系数RF随着整流机组负荷电流的增大而不断增大，并且随着电抗系数RF的增大，整流机组工作在不同的区间上。下面是12脉波整流机组直流输出电压的调整特性

在简化计算中，首先将各个区间的外特性曲线线性化，即用连接起点与终点的线段代替该曲线，求出线段直线表达式。之后将整流机组等效为带内阻的电压源，其中内阻为直线表达式的斜率，电压源值为直线表达式的截距。整流机组等效电路图如图1所示

Vd1→d2的电流分界点

图1 整流机组的等效模型

Vd2→d3的电流分界点

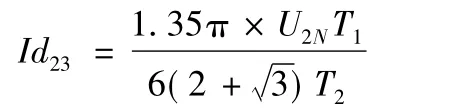
Vd3→d4的电流分界点

Vd4→d5.1的电流分界点

Vd5.1→d5.2的电流分界点

2 直流牵引供电系统的数学模型

直流牵引网上、下行线路双边并列供电时，牵引网发生短路的化简等值电路如图2所示:

考虑接触网为均匀结构，设r为馈电线每公里电阻值，rp为走行轨电阻，两变电所的间距为L，短路点到A变电所的距离是Ld，为了方便求出短路电流值Id，将图2中整流机组用等效电压源和电阻表示，并对上下行接触网电阻进行Y形变换，便得到图3。其中

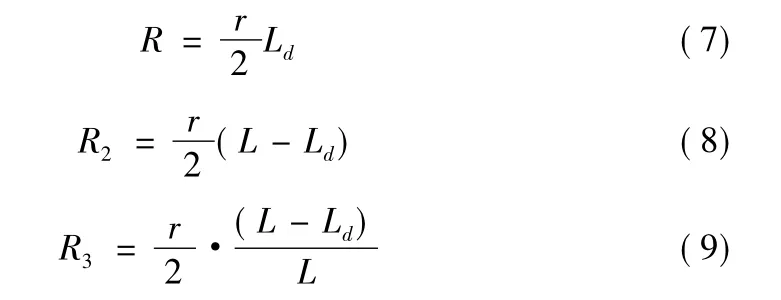
3 两变电所间短路稳态电流的计算

3.1 两变电所间短路稳态电流的计算

如图3所示，两牵引变电所间任意一点发生短路时，运用基尔霍夫定律可以分别求出两个变电所提供的短路电流Id1和Id2，将两个电流相加，就能得到总的短路电流。

3.2 计算机算法与流程

由式子(11)和(12)可见，求短路稳态电流值时，确 定 Ua、Ub、ReqA和ReqB是关键，本文给出了迭代求整流机组工作区间的方法，其迭代求解过程如图4。

(1)输入原始数据，计算耦合系数，换 相 电抗、整流机组的工作区间数及各工作区间的临界电流。

(2)默认A、B变电所都工作在第一工作区间。

(3)由式子(11)和(12)计算每个变电所提供的短路电流。

(4)判断计算的短路电流是否在各个工作区间的电流范围之内，如果是，进入步骤;

(5)如果不是，调整工作区间，继续进入步骤(3)，直到所有的整流机组的工作区间不需要调整。

(6)输出短路计算结果。

3.3 仿真界面的实现

按照上面的算法，采用Visual C#开发工具编制直流牵引供电网络短路电流计算的界面，用户通过界面输入原始数据，即可得到变电所的等效信息和短路点的稳态短路电流值，同时也能输出excel表格，对excel表格进行处理，就可以得到牵引网短路点位置与短路电流的关系图。程序主界面如图5所示。

图5 程序主界面

4 仿真实例

本文以上海地铁3号线接触网发生近端、中端和远端短路试验为例进行仿真，具体试验内容参见文献［5］，并同西南交通大学开发的SimSystem软件的仿真结果［3］进行对比。输入仿真数据如表1所示。

表1 上海地铁3号线的基本数据

短路点位置与短路电流的关系图如图6所示。仿真结果与实验数据及SimSystem仿真数据的比较如表如表2所示。

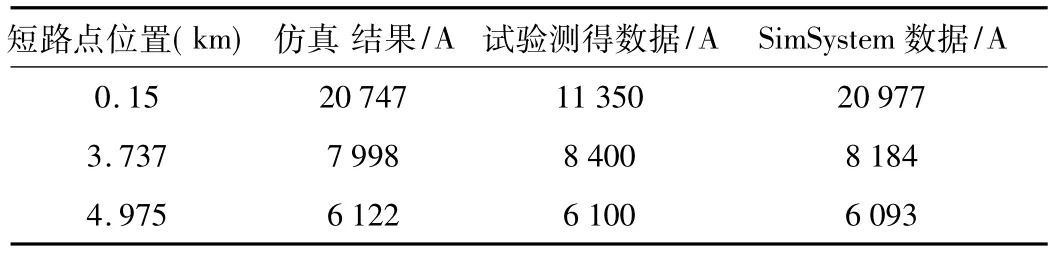
表2 仿真结果与试验数据及SimSystem仿真数据的比较

对上面结果分析可见，仿真数据和试验数据及SimSystem仿真数据大致相同，短路点距离变电所较远时，仿真数据跟实测数据差别很小，但是短路点距离变电所较近时数据相差很大，这是因为在变电所附近发生短路时，继电保护装置迅速动作，使得试验测量的数值不能正确反映实际稳态短路电流的情况。由上可见，该软件能够用于计算直流牵引供电系统短路电流的稳态值。

下面结合北京地铁6号线北海公园和东四牵引变电所的情况，对直流牵引网上下行双边并列供电时，接触轨发生短路情况进行仿真，输入仿真数据见表3所示。

图6 稳态计算结果

表3 北京地铁6号线的基本数据

短路点位置与短路电流的关系图如图7所示。

由图7可见，每个牵引变电所提供的短路电流值随短路点与变电所距离的增大而逐渐减小，并且短路点距离越大，短路电流值减小的幅度越不明显;总的短路电流稳态值为临近两个变电所提供的短路电流值的叠加，并且其数值是先减小后增大，在短路点位于两个牵引变电所距离一半的时候最小。

图7 直流牵引网双边供电短路稳态电流

5 结束语

本文所编写的应用程序可较为准确的反映直流牵引供电系统短路电流的情况，但本文所采用的数学模型只考虑了短路点临近两个变电所提供的短路电流而忽略了远方变电所对短路点的影响，另外本文所采用的数学模型只是简化模型，为了提高计算的准确性，这就要求在建立数学模型时，还应考虑整个牵引网络对短路点的影响、钢轨对地的过渡电导、杂散电流收集网等诸多因素。

［1］曹建设，杲秀芳.直流牵引网短路电流计算［J］.城市轨道交通，2007(8):31-34.

［2］乌正康，杨其华.地铁牵引供电网短路稳态仿真分析［J］.铁道学报，1993(3):39-44.

［3］李良威，李群湛.24脉波整流器外特性仿真及其在城市轨道交通中的应用［J］.城市轨道交通，2007(2):52-55.

［4］齐兵，徐鸿滨.城市轨道交通供电系统直流短路试验［J］.电气化铁道，2002(1):50-51.

［5］苏保卫，张永康.上海轨道交通3号线供电短路试验［J］.城市轨道交通研究，2005(3):68-70.