共归纳数据类型上的共递归操作及其计算定律*

苏锦钿 余珊珊

(1.华南理工大学计算机科学与工程学院，广东广州510006;2.中山大学信息科学与技术学院，广东广州510275)

归纳数据类型是类型理论的一个重要组成部分和研究重点.程序语言中的有限分支树、数组、队列、堆栈和自然数等都是典型的归纳数据类型.这一类数据类型的语法构造可以通过一些称为“构造子”的操作进行归纳地描述.从代数的角度来看，每一个归纳数据类型可以看成是某个代数函子下的一个初始代数，其中代数函子对应着该数据类型的构造操作.由初始代数的初始性可定义归纳数据类型上的一个递归操作，称为折叠操作［1］或 catamorphism［2］，且该操作满足一系列的代数计算定律.递归操作及其计算定律在程序的计算及转换研究中具有非常重要的作用［3-4］.

共归纳数据类型［5］也称为共代数数据类型［6］或共数据类型［7-8］，是近十几年来类型理论中研究数据类型的一种新思路，可看作是归纳数据类型的范畴对偶概念.与归纳数据类型不同，共归纳数据类型侧重于研究数据类型在运行过程中所展现出来的(特别是无限)动态行为，例如流、链表、无限分支树或无限数组等.这一类具有动态行为特征的数据类型可以进一步抽象为某个共代数函子下的一个终结共代数，其中共代数函子对应着该数据类型上的观察操作.由终结共代数的终结性可定义该数据类型上的一个共递归操作，称为 unfold［9-10］操作或 atamorphism［2］，并且该操作满足一系列的共代数计算定律.由于共递归操作及其计算定律在基于行为特征的函数定义或程序推理及转换过程中具有重要的作用，因此 Greiner 等许多学者［5，8，11-15］均对共递归操作及其计算定律进行了比较深入和全面的研究.这些研究的基本思路是将共归纳数据类型看作某个共代数函子下的终结共代数，从而利用终结共代数及共归纳原理给出共递归操作上的各种计算定律.但这些研究对参数化共归纳数据类型上的计算定律的分析较为简单，没有考虑自然转换下不同类型函子上的计算定律.

因此，文中从范畴论的角度给出共归纳数据类型的共代数描述，并结合实例对共归纳数据类型上的共递归操作及其计算定律进行分析，特别是利用双函子及类型函子对参数化共归纳数据类型进行抽象描述，并给出类型函子上的计算定律及其证明.

1 共归纳数据类型

作为归纳数据类型的范畴对偶概念，共归纳数据类型关注的不是数据类型的语法构造，而是数据类型在执行的过程中所展现出来的外部动态行为特征.

例1 下面是程序语言中一些典型的共归纳数据类型.

(1)流.用于描述输入/输出设备与程序之间交互关系的流一般包含两个操作，一个操作value:AN→A用于得到流当前状态所能显示的值(假设值的类型为A，则无限流可表示为AN，其中N为自然数)，另一个操作next:AN→AN则使流进入下一个状态:

(2)链表.对于一个由空链表nil和插入操作cons递归定义而成的参数化链表(假定链表中元素的类型为A，A∞=AN∪Aω是由无限链表AN和有限链表Aω所构成的集合)，可通过两个操作head和tail进行观察，其中head:A∞→1+A用于获取链表的头部元素，tail:A∞→1+A∞用于返回链表中除头元素外的剩余元素.若数组为空，则两个操作均返回⊥∈1:

(3)二叉树.对于以A中元素为标签的二叉树btree(A)，可通过以下的操作进行观察:

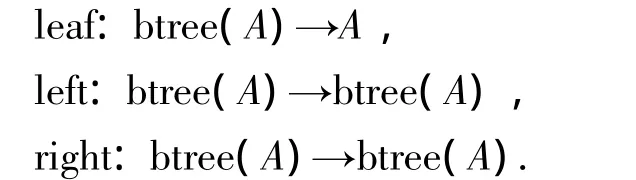
其中leaf操作给出了根节点上的标签，left和right则分别返回以左右结点为根的二叉树.

从上述例子可以看出，共归纳数据类型是由某个数据类型集合及其上的一组析构操作所构成，其中析构操作给出了对数据类型的观察结果.对于给定的共归纳数据类型X，其上的析构操作σ通常具有σ:X→A1×A2×…×An的形式，其中Ai为某个已知的数据类型，表示对X的一种观察结果.

作为代数的范畴对偶概念，共代数本质上也可以看成是由集合及其上一组满足一定性质的操作所构成，通常具有αX:X→FX的形式.在计算机科学中，共代数常被看成是具有内部状态的系统，X是系统中所有可能状态的集合，基调αX是对系统的一种观察.

定义1 给定集合范畴Set及其上的一个自函子F:Set→Set，一个 F-共代数定义为一个二元组(X，αX:X→FX)，其中X是Set中的对象，称为该F-共代数的载体，αX:X→FX是Set中的射，称为该F-共代数的变迁射或基调.任意两个F-共代数(X，αX:X→FX)和(Y，αY:Y→FY)之间的同态射 f:(X，αX)→(Y，αY)是 Set中的射 f:X→Y，且满足图1 所示的图表交换.

图1 共代数同态射Fig.1 Homomorphism between coalgebras

由于共归纳数据类型本质上也是由集合及其上一组满足某些性质的操作所构成，因此可以进一步抽象为某个共代数，其中共代数函子对应着该数据类型上的析构操作.

例2 流、链表和二叉树等共归纳数据类型都可以表示为共代数.

(1)流可以表示为函子SA(X)=A×X下的共代数(X，αX=〈value，next〉:X→A ×X)，X 为流中所有可能状态的集合.

(2)链表可以表示为函子LA(X)=A×X+1下的共代数(X，αX=〈head，tail〉:X→A ×X+1).

(3)二叉树可以表示为函子BA(X)=A×X×X下的共代数(X，αX=〈leaf，right，right〉:X→A × X ×X).

共归纳数据类型不仅可以抽象地描述为共代数，而且是对应共代数函子上的最大固定点，即为该函子的一个终结共代数，记为(vF，outF:vF→FvF).该终结共代数实际上就给出了共归纳类型的定义.

例如，流可以看成是函子SA(X)=A×X下的一个终结共代数(AN，〈value，next〉:AN→A × AN)，链表可以看成是函子LA(X)=A×X+1下的一个终结共代数(A∞，〈head，tail〉:A∞→A × A∞+1)，二叉树可以看成是函子BA(X)=A×X×X下的一个终结共代数(btree(A)，〈leaf，left，right〉:btree(A)→A ×btree(A)×btree(A))，其中btree(A)是由A中的元素所构成的无限二叉树结构.

根据文献[16]中的定理9.1可得到终结代数上的一个重要性质.

定理1(文献[16]中定理9.1)终结共代数上的基调是一个同构射.

即基调 outF:vF→FvF是一个同构射，其逆outF－1:FvF→vF给出了载体集vF上的构造操作.例如，函子FX=A×X的终结共代数上的基调outF=〈value，next〉的逆 outF－1=［scons］为流上的一个构造操作，其中scons:A×X→X表示将一个类型为A的元素作为前缀添加到一个流中.文献［17］中指出在许多情况下函子F的终结共代数(vF，outF)可以理解为同一函子下的初始代数(μF，inF:μF→FμF)的某种形式的补充.例如，有限及无限链表集A∞可看成是函子FX=1+A×X下只包含有限链表Aω的初始代数的一种补充.事实上，根据上述定理1可将(vF，outF)的逆(vF，outF－1)看成是一个代数.但这容易使得对共归纳原理的形式化描述变得更加复杂，而且也不符合共代数的非良基集性质.

2 共递归操作及其计算定律

由终结共代数的终结性可以定义每一个共归纳类型上的一个操作，用于表示由该类型上的结构化共递归定义而成的函数，称为unfold操作或atamorphism.该函数就是由任意的F-共代数(X，αX)到其终结共代数(vF，outF)的唯一同态射，记为[αX]F:X→vF.由于[αX]F为一个共代数同态射，因此满足等式:outF◦[αX]F=F[αX]F◦αX，即得如图 2 所示的图表交换.

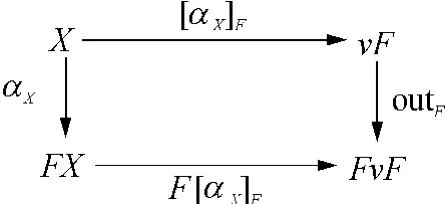
图2 终结共代数及其unfold操作Fig.2 Final coalgebras and its unfold operation

由终结共代数的终结性可以得到著名的共归纳原理(包括共归纳定义原则和证明原则).

(1)共归纳定义原则 要定义一个以终结共代数载体集为目标的函数，只要根据所定义的函数所应满足的性质，为该函数的源构造一个合适的共代数即可;

(2)共归纳证明原则 要证明两个以终结共代数载体集为目标的函数相等，只需要证明这两个函数都是同一共代数到终结共代数的同态即可.

例3 例1中的各个共归纳数据类型上的unfold操作分别定义为

(1)对于任意的流共代数(X，αX=〈vs，ns〉:X→A×X，unfold操作为唯一射 f=[αX]SA:X→AN，满足value ◦f=vs和 next◦f=f◦ns.

(2)对于任意的链表共代数(X，αX=〈hd，tl〉:X→A×X+1，unfold为唯一射 f=[αX]LA:X→A∞，使得满足 head ◦f=hd 和 tail◦f=f◦tl.

(3)对于任意的二叉树共代数(X，αX=〈lf，lt，rt〉:X→A×X ×X)，unfold为唯一射 f=[αX]BA:X→btree(A)，使得满足 leaf◦f=lf、left◦f=f◦lt和 right◦f=f◦rt.

共归纳数据类型上的unfold操作满足以下的共代数计算定律［2］.

定律1(单元定律)若unfold操作的源是终结共代数，那么该unfold操作为单元射，即:[outF]F=IdvF.

证明由任意的单元射IdvF:vF→vF都为同态射及unfold操作的唯一性可知[outF]F=IdvF成立.

定律2(unfold-map融合定律)对一个unfold操作和一个共代数同态射进行复合后仍然为一个unfold 操作，即:αY◦f=Ff◦αX⇒[αY]F◦f=[αX]F.

证明由前提可知下图3中的左、右部分均满足图表交换.因此，[αY]F◦f和[αX]F为共代数(X，αX)到终结共代数(vF，outF)的 unfold操作.由 unfold 操作的唯一性可知有 αY◦f=Ff◦αX⇒[αY]F◦f=[αX]F.证毕.

图3 共代数同态射及其unfold操作Fig.3 Homomorphism between coalgebras and its unfold operation

unfold-map融合定律在程序计算中具有重要的作用，可以用于消除计算过程中所产生的中间数据结构，从而简化程序计算的结构.

例4 自然数流上的倍乘函数double:NatN→NatN将流中的每一个自然数元素都乘以2后构成一个新的流:

显然，double:(NatN，〈vl，nt〉)→(NatN，〈value，next〉)是自然数流之间的一个共代数同态射，且double 为一个 unfold 射[〈vl，nt〉]SA.

函数merge:NatN×NatN→NatN依次交替地将两个自然数流中的头元素取出，并构成一个新的流，即merge(a1:x1，x2)=a1:merge(x2，x1).显然，merge 满足以下等式:

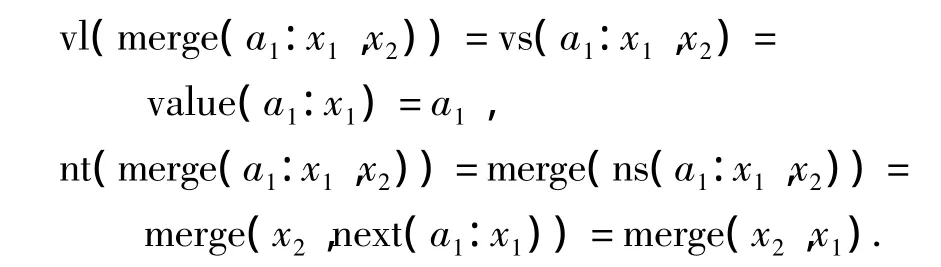
因此，merge:(NatN× NatN，〈vs，ns〉)→(NatN，〈vl，nt〉)是一个同态射.对函数 double和 merge进行合并可得到以下等式:

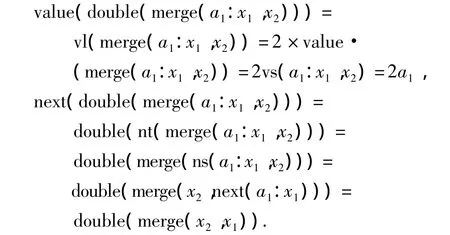
double◦merge表示先利用merge将两个自然数流合并在一起，然后再将double函数作用于该流，最终得到一个新的自然数流.

根据unfold-map融合定律可以不需要merge和double函数，而是直接利用函数 dmerge:(NatN×NatN，〈vs，ns〉)→(NatN，〈value，next〉)依次交替地将两个自然数流中的头元素取出并乘以2后构成一个新的流，即

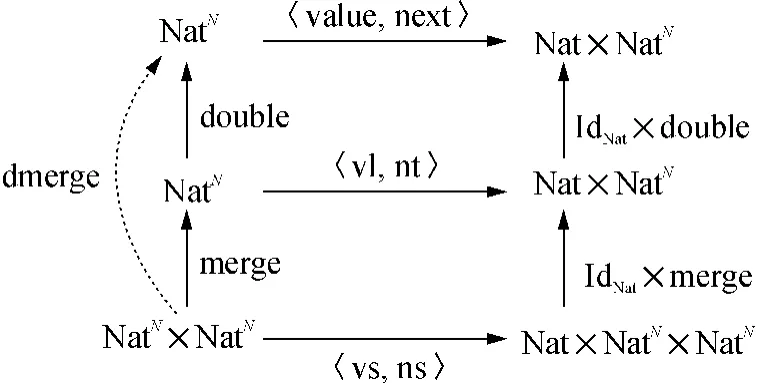
图4 基于unfold-map融合定律的流实例Fig.4 Examples of stream for unfold-map fusion law

最后一个定律称为unfold-unfold定律，用于对产生并且消耗一个中间共代数结构的函数进行结合.应用该定律时，要求中间的共代数结构必须是由一个unfold操作产生的，并且该unfold操作的目标共代数是通过一个自然转换构造而成.

所谓的自然转换是指函子间的一个转换函数τ:F⇒G，将一个 F-共代数转换为一个 G-共代数，使得:若f:X→Y 为F-共代数(X，αX:X→FX)和(Y，αY:Y→FY)间的同态射，则 f同时为 G-共代数(X，τX◦αX:X→GX)和(Y，τY◦αY:Y→GY)间的同态射，即满足 Gf◦τX◦αX=τY◦αY◦f.

直观地说，一个自然转换τ:F⇒G可看成是一个多项式函数，将某一类共代数转换成另一类共代数.

定律3(unfold-unfold融合定律)给定一个自然转换关系τ:F⇒G，对于 F-共代数(X，αX)，有:

证明对于任意的 F-共代数(X，αX)，由于unfold操作是一个同态射，根据自然转换和unfold的性质可知图5中的各个图表均满足交换.[τvF◦outF]G◦[αX]F和[τX◦αX]G均为 G-共代数(X，τX◦αX)到G-终结共代数(vG，outG)的unfold操作.由unfold操作的唯一性可知[τvF◦outF]G◦[αX]F=[τX◦αX]G.证毕.

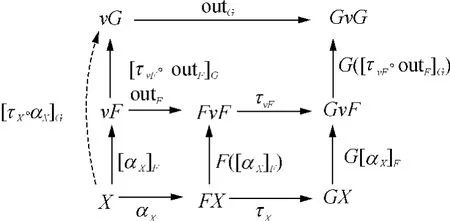
图5 unfold-unfold融合定律Fig.5 Unfold-unfold fusion law

3 参数化共归纳数据类型

上述的流、链表和二叉树等共归纳数据类型通常都是参数化的，因此可以进一步抽象为某个双函子F:Set→Set×Set下的共代数.通过固定双函子F的共域中的第1个参数(假设该参数的类型为A)，可得到一个一元函子F:Set→A×Set，记为FA，使得FAX=FA(A，X).设DvA是由FA所确定的终结共代数上的载体，则Dv:Set→Set可以提升为一个类型函子［3］，使得对于任意的 f:A→B，有:Dvf=[F(f，IdDvA)◦outFA]FB，如图 6 所示.

图6 类型函子Fig.6 Type functor

例5 若Dv为流类型构造子，则对于类型A有DvA=AN，对于射 f:A→B 有:Dvf=fN=[〈f◦value，next〉]SB:AN→BN;若 Dv为链表类型构造子，则对于类型A有 DvA=A∞，对于射f:A→B有:Dvf=f∞=[〈f◦head，tail〉]LB:A∞→B∞;若 Dv为一个二叉树类型构造子，则对于类型A有DvA=btree(A)，对于射f:A→B 有:Dvf=btree(f)=[〈f◦leaf，left，right〉]BB:btree(A)→btree(B).

类型函子Dv满足相应的unfold-map融合定律.

图7 类型函子的unfold-map融合定律Fig.7 Unfold-map fusion law for type functor

定律4(类型函子上的unfold-map融合定律)对于 f:A→B 和 g:X→FAX，有:Dvf◦[g]FA=[F(f，IdX)◦g]FB.

证明 根据前提可知上述图中的各个图表均满足交换.Dvf◦[g]FA和[F(f，IdX)◦g]FB均为共代数(X，F(f，IdX)◦g)到(DvB，outFB)的 unfold 操作.由unfold 的唯一性可知 Dvf◦[g]FA=[F(f，IdX)◦g]FB.证毕.

定理2 对于两个双函子F，G:Set→Set×Set，设τ:F⇒G 为一个自然转换，τA，X表示 τA，X:FAX⇒GAX，则对于 g:X→FAX，有 τA，X◦g:X→GAX，且对于f:A→B有:

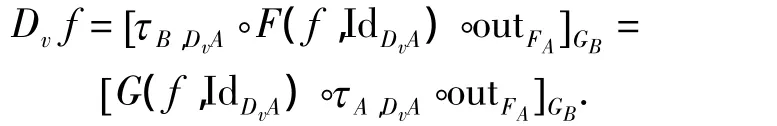
证明 由类型函子的性质及unfold操作的唯一性可证明成立.

在自然转换的作用下，类型函子Dv满足相应的unfold-unfold融合定律，如图8所示.

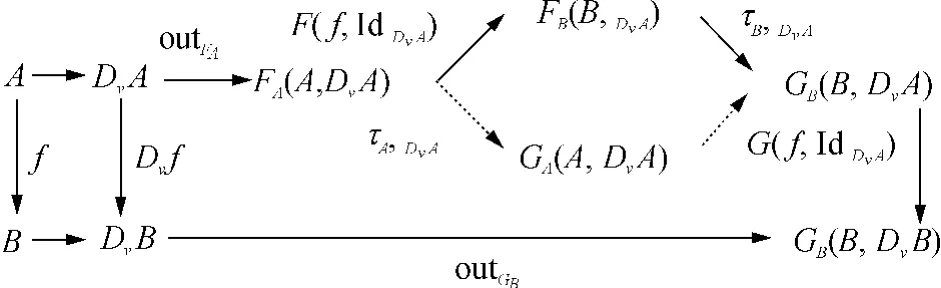
图8 自然转换下的类型函子Fig.8 Type functor via natural transformation

定律5(类型函子上的unfold-unfold融合定律)对于f:A→B、g:X→FAX及自然转换τ:F⇒G，有:

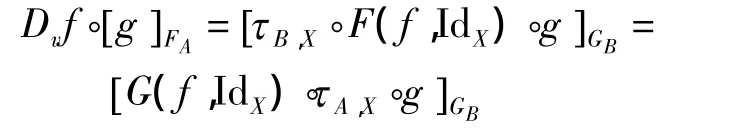
证明由unfold的定义及自然转换保持态射和组合关系的性质可知，Dvf◦[g]FA=[τB，X◦F(f，IdX)◦g]GB和[G(f，IdX)◦τA，X◦g]GB均为共代数(X，G(f，IdX)◦τA，X◦g)到(DvB，outGB)的 unfold 操作，因此由其唯一性可证明上述等式成立.证毕.

其融合定律如图9所示.

图9 类型函子上的unfold-unfold融合定律Fig.9 Unfold-unfold fusion law for type functor

4 结语

对共归纳数据类型上的共递归操作及其计算定律进行研究有助于人们更加深入地了解抽象数据类型的动态行为特征，提高程序语言对其动态行为的描述能力.更重要的，可以将终结共代数及共归纳原理等共代数理论引入到类型理论中，便于在程序中定义更加复杂的函数或开展基于行为特征的推理或转换工作.

在下一步工作中，将对其它的共递归操作(例如原始共递归和Course-of-value共递归等)及其计算定律进行深入的研究.

［1］Bird R.Introduction to functional programming using haskell［M］.2nd edition.UK:Prentice-Hall，1998.

［2］Meijer E，Fokkinga E，Paterson R.Functional programming with bananas，lenses，envelopes and barbed wire［C］∥Functional Programming Languages and Computer Architecture.Berlin:Springer，1991:215-240.

［3］Bird R，Moor O D.Algebra of programming［M］.UK:Prentice Hall，1997.

［4］Gibbons J.Lecture notes on algebraic and coalgebraic methods for calculating functional programs［C］∥Summer School on Algebraic and Coalgebraic Methods in the Mathematics of Program Construction.UK:Oxford，2000.

［5］Greiner J.Programming with inductive and co-inductive types［R］.Pittsburgh:School of Computer Science，Carnegie-Mellon University，1992.

［6］Hensel U，Jacobs B.Coalgebraic theories of sequences in PVS ［J］.Journal of Logic and Computation，1999，9(4):463-500.

［7］Kieburtz R B.Codata and comonads in Haskell［EB/OL］.(1999-12-31).http:∥citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.46.5169.

［8］Hinze R.Reasoning about Codata［C］∥Proceedings of centraleuropean functionalprogramming school-third summer school.Berlin:Springer Berlin Heidelberg，2010:42-93.

［9］Hutton G.Fold and unfold for program semantics［C］∥Proceedings of the 3rd ACM Sigplan International Conference on Functional Programming.［S.l.］:ACM，1998:280-288.

［10］Gibbons J，Jones G.The under-appreciated unfold ［C］∥Proc 3rd ACM Sigplan International Conference on Functional Programming.New York:ACM，1998:273-279.

［11］Harper R.Practical foundations fro programming languages［M］.［S.l.］:Carnegie Mellon University，2010.

［12］Vos T.Program construction and generation based on recursive types［D］.Utrecht:University of Utrecht，1995.

［13］Vene V，Uustalu T.Functional programming with apomor phism(Corecursion)［J］∥Proceedings of the Estonian Academy of Science:Physics，Mathematics，1998，47(3):147-161.

［14］Uustalu T，Vene V.Primitive(Co)recursion and course-of-value(Co)iteration，categorically ［J］.Informatica，1999，10(1):5-26.

［15］Vene V.Categorical programming with inductive and coinductive types［D］.Estonia:Department of Computer Science，University of Tartu，2000:1-100.

［16］Rutten J J M M.Universal coalgebra:a theory of systems［J］.Theoretical Computer Science，2000，249(1):3-80.

［17］Barr M.Terminal coalgebras in well-founded set theory［J］.Theoretical Computer Science，1993，114(2):299-315.