基于表面势的有机薄膜晶体管漏电流的解析模型*

吴穹 姚若河 刘玉荣

(华南理工大学电子与信息学院，广东广州510640)

近年来，有机薄膜晶体管(OTFT)因在柔性显示、低成本大面积有机电子器件等领域具有广阔的应用前景而受到广泛的关注［1］.OTFT无论是作为像素控制单元，还是作为外围驱动电路，其电流模型对于电路模拟都是关键技术之一.

早期的OTFT电流模型主要是基于阈值电压的模型［2-4］，往往是在基于阈值电压的场效应晶体管(MOSFET)电流模型的基础上，加上相关的经验参数来描述OTFT的电流特性.基于阈值电压的模型定义阈值电压的方法不明确，降低了精确度;而且各分区之间需要使用光滑函数连接，不能准确地描述电流特性及各工作区之间的过渡状态.近年来，基于表面势的电流模型因具有精度高、无需光滑函数、能同时描述亚阈区和开启区电流等优点，逐渐成为研究的热点［5-7］.

Torricelli等［7］报道了基于表面势的OTFT电流模型，但该模型存在如下不足:(1)通过表面势隐含方程求解表面势时采用了近似计算，近似计算结果与数值计算结果相比，存在较大的误差，精度有待提高;(2)该模型推导出的电流表达式包含两项，未能区分扩散电流和漂移电流，仅在最后忽略其中较小的一项以得到紧凑的电流表达式.

为此，文中首先运用薄层电荷方法，分别推导出扩散电流和漂移电流表达式，然后运用泰勒展开，给出了隐含方程中表面势的解析求解方法，最后得到基于变程跳跃载流子输运模式下的解析电流模型，并通过仿真验证该模型的有效性.

1 扩散与漂移电流

为简单起见，文中仅针对沟道不掺杂的n沟道OTFT器件，且器件工作于积累模式［7］.对于p沟道器件，作适当延伸即可.对于OTFT，陷阱态对器件性能有重要的影响，因此其电流模型的建立过程需考虑带隙中陷阱态的分布状况.对于OTFT，指数分布的陷阱态密度已经被业界普遍接受和实验证实［8-10］，因此模型中考虑带隙中陷阱态密度为指数分布.对于n沟道器件，处于禁带上半部分的受主陷阱态决定其电学特性，陷阱态密度gTA可以表示为

式中，E为电子能量，Ei为本征费米能级，gAD为本征费米能级处的陷阱态密度，k为玻尔兹曼常数，T0为指数分布陷阱态密度的特性温度.

一维泊松方程表示为

式中，q为电子电量，ψ为电势，x为位置，εs为沟道材料的介电常数，n为自由电荷浓度，NTA为陷落于陷阱态的电荷浓度.

自由电荷浓度表示为

式中:nX=为OTFT中的本征电子浓度，EF0为体区中性薄膜中电子的费米能级，对于沟道不掺杂的TFT，EF0位于禁带中央附近;φt=kT/q，T为热力学温度;Vch为准费米势.

陷落电荷浓度表示为［5-7］

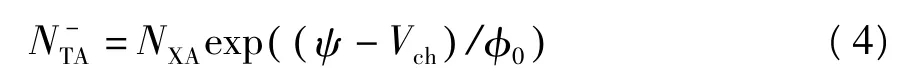
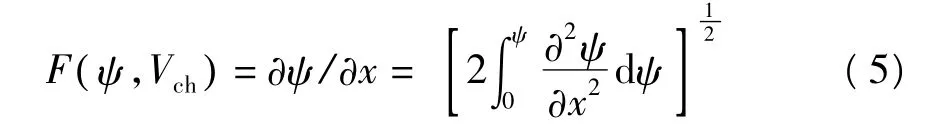
把式(2)代入式(5)，运用近似 exp(ψ/φt)≫1和可得

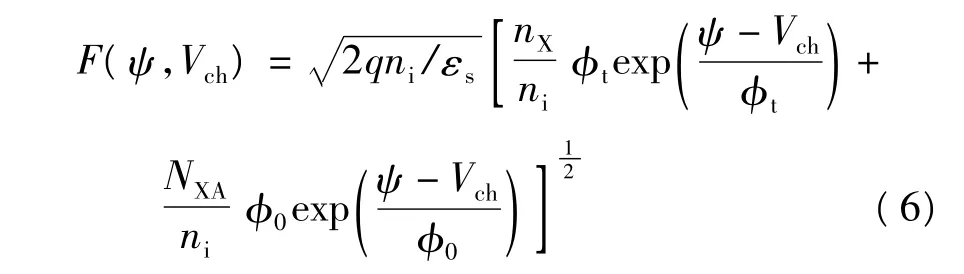
在栅氧与沟道界面运用高斯定理，可得

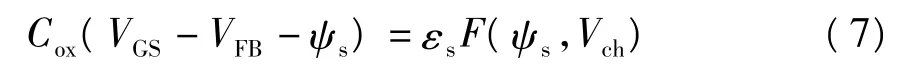
式中:Cox=εox/tox，εox为栅氧的介电常数，tox为栅氧厚度;VGS为栅电压;VFB为平带电压;ψs为表面势.

把式(6)代入式(7)，可得表面势方程:

其中γ=

自由电荷可以表示为

陷落电荷可以表示为

最后，由Pao-Sah模型表示的电流表达式为［11］

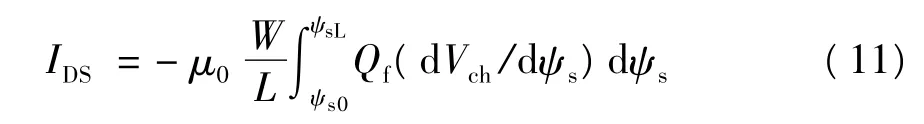
式中，μ0为OTFT中电子的带迁移率［10］，W和L分别为沟道的宽度和长度，ψs0和ψsL分别为源端和漏端的表面势.

为了分离扩散电流和漂移电流，采用文献［11］中的计算方法，由式(8)可得

把式(12)代入式(11)，可得扩散电流为

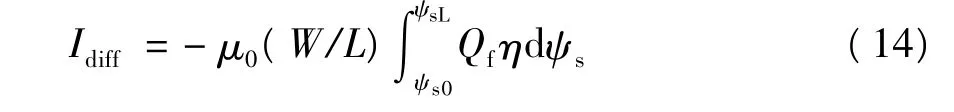
漂移电流为

在OTFT的沟道中，存在高的陷阱态密度，自由电荷浓度远小于陷落于陷阱态的电荷浓度，这与非晶硅薄膜晶体管(a-Si TFT) 类似［7，12］，因此忽略式(6)等号右边的第一项，将其代入式(10)，陷落的电荷近似为

自由电荷近似为

由于自由电荷浓度远小于陷落于陷阱态的电荷浓度，对式(8)进行泰勒展开，得

把式(16)和(18)代入式(17)，可得

由于自由电荷浓度远小于陷落于陷阱态的电荷浓度，这类似于MOSFET器件工作于亚阈区的情形，其中陷落电荷决定表面势方程［11］，式(8)简化成

把式(20)代入式(19)，消去Vch，自由电荷为

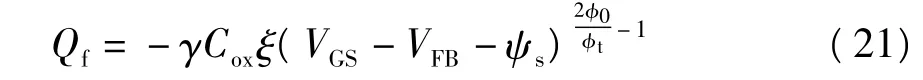
把式(16)和(17)代入式(13)，η整理为

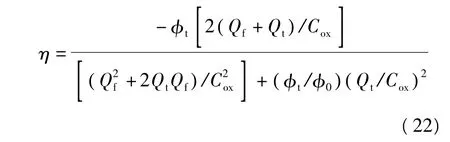
由于自由电荷浓度远小于陷落于陷阱态的电荷浓度，对式(22)，运用Qf≈0可得

由式(14)、(16)、(19)、(23)推导出扩散电流:

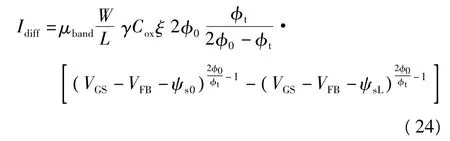
式中，μband为带迁移率，ψs0和ψsL由式(20)解出.

把式(21)代入式(15)，推导出漂移电流:

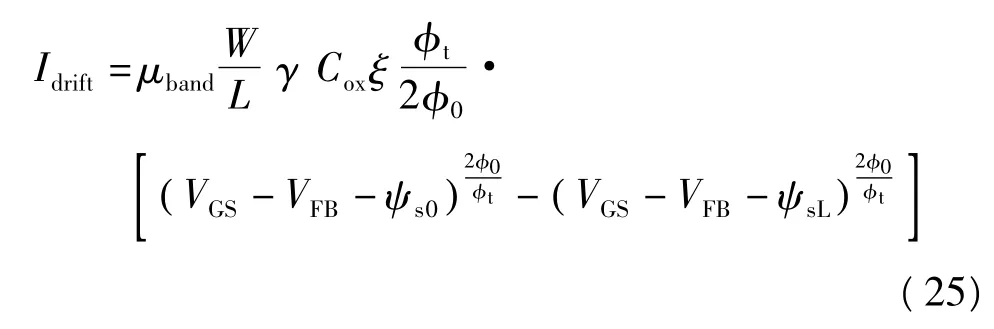
注意到在文献［7］中，其推导出的电流表达式是式(24)与(25)之和，并没有区别扩散电流和漂移电流，而且采用近似计算来求解，其与数值计算结果偏差较大.

2 表面势的解析求解

为了得到式(24)和(25)所表示的精确电流模型，需要对表面势隐含方程式(20)中的表面势进行精确求解.对式(20)进行归一化处理，可得到

式中，xg=x=为待求项.

式(26)变形，可得

其中θ为误差项，θ≈0.

式(28)整理为

由式(29)解得

且由式(26)可知

因式(30)和(31)仅为式(26)的近似解，为提高精度，可以对误差项θ加以考虑［13］.式(26)的新解为

把式(32)代入式(26)，得

因θ≈0，对式(33)中的 exp(θ)进行泰勒展开，得

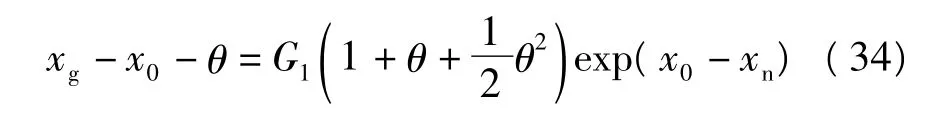
由式(34)即可解得误差项θ，因此式(32)的解有较高的精度.同理，可以进行二次误差修正，将x2=x1+θ'代入式(26)再进行泰勒展开，可以获得更高精度的解.

3 结果与讨论

前面着重进行了电荷分析和表面势的求解，为了得到适用于OTFT的解析电流表达式，还需要考虑OTFT中电荷的输运机理，现今主要有两种理论:(1)多重陷落与释放(MTR)理论［2-3］;(2)变程跳跃(VRH)理论［5-7］.由于 MTR 理论存在的局限性［14］，近年来人们更多地应用VRH理论来解释OTFT中载流子的输运机理，因此文中采用VRH理论来分析OTFT的电流电压特性.

在式(24)和(25)中，相关参数与文献［5］中的参数β对照可得

式中:σ0为渗透因子;α为局域态之间的有效波函数重叠参数;Bc为渗透起始时的临界数目，对于三维的非晶态系统，Bc≅2.8［5-7］.

扩散电流表示为

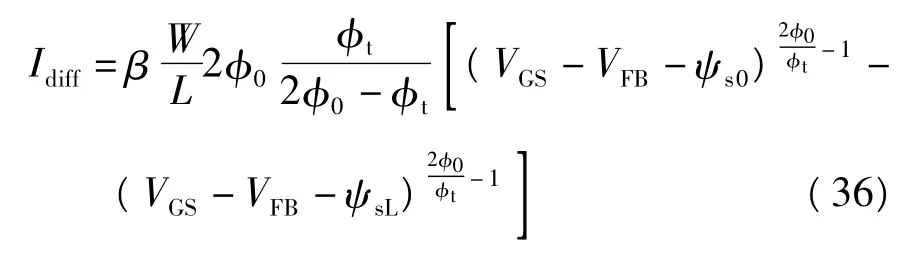
漂移电流表示为

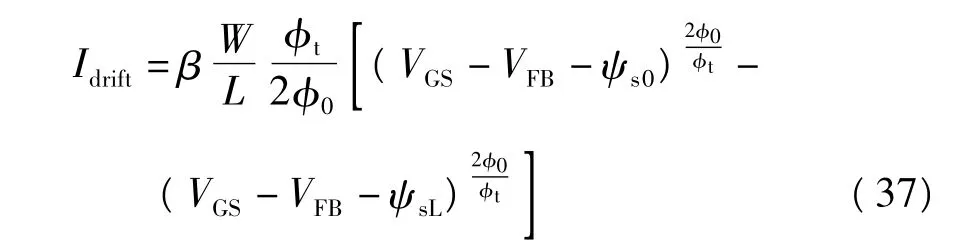
为得到表面势与栅电压之间的变化关系，可采用两种方案来求解:(1)对表面势的隐含方程(20)进行数值求解;(2)通过二次误差修正后所得的解析式进行精确求解.在解析求解过程中，由于采用了泰勒展开，而且仅计入二次误差修正，因而计算结果存在一定的误差，相对误差可表示为

式中，ψsA和ψsN分别为解析计算和数值计算的误差.

图1给出了不同准费米势下表面势与栅电压之间的变化关系及解析求解的相对误差.从图1(b)可看出，采用文中解析方法计算的表面势更加准确.

图2给出了采用文中模型计算得到的扩散和漂移电流.由图2可知，漂移电流主导OTFT的转移特性，扩散电流可以忽略，这在文献［15］中有提及，但没有给出具体的推导过程.漂移电流主导OTFT的转移特性的原因是，OTFT薄膜的带隙中存在指数分布的陷阱态密度.

为了验证模型的准确性，利用式(37)分别对基于并五苯和聚噻吩基-乙烯化合物(PTV)的两种OTFT的转移特性和温度特性进行仿真计算，并与实验数据［7］进行比较，结果如图3所示.计算过程选用了与文献［7］中相同的参数，如表1所示.

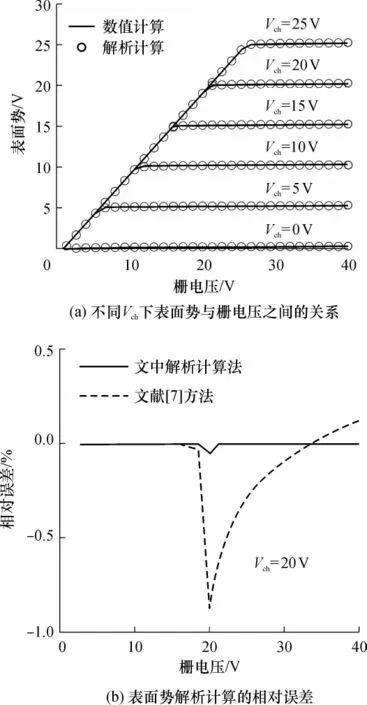
图1 表面势的解析计算与数值计算结果对比Fig.1 Comparison of surface potential between analytical and numerical calculations

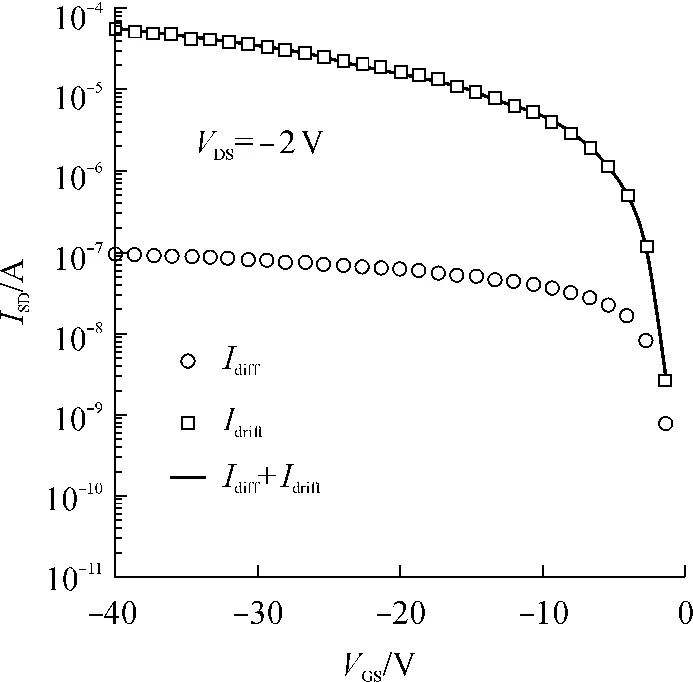
图2 OTFT的扩散电流与漂移电流Fig.2 Diffusion and drift currents of OTFT

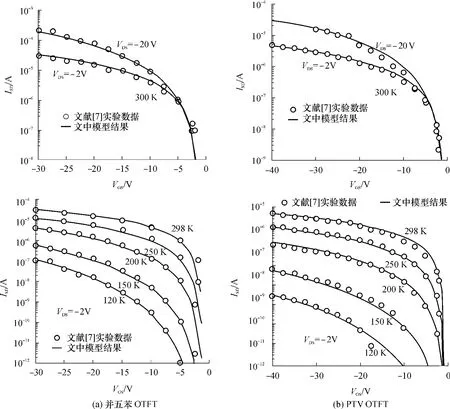
图3 两种OTFT的转移特性曲线比较Fig.3 Comparison of transfer characteristics curves of OTFTs

表1 计算中所用的参数值Table 1 Parameters used in the caculation

从图3可以看出:(1)两种不同有机材料制备的OTFT都具有与MOSFET相似的特性，即电流随着栅电压(绝对值)和漏电压(绝对值)的增大而增大，且计算结果与实验数据相吻合.(2)并五苯OTFT的电流要比PTV OTFT的电流约大两个数量级，与文献［16］中的报道相一致，这主要与局域态之间的有效波函数重叠参数α有关［16］.PTV材料属于聚合物材料，而并五苯属于小分子材料.并五苯具有更好的层叠特性，电子的波函数大面积重叠，导致α-1值较大，因此电流较大［16］.(3)对于两种OTFT，电流都随着温度的增大而明显增大，这是由载流子的变程跳跃输运机理决定的，即电荷输运由载流子在局域态之间的热激活特征的隧穿主导［7，16］.所谓变程跳跃，就是指载流子可能短程跳跃而表现出高的激活能，或者长程跳跃表现出低的激活能［7，16］.温度升高，导致载流子的长程跳跃加剧，因此电流增加.

4 结语

考虑带隙中陷阱态密度指数分布，文中基于变程跳跃电荷输运理论，并利用表面势的解析求解，提出了基于表面势的OTFT电流解析模型.仿真结果与实验数据对比表明，在OTFT的电流中漂移电流占主导，扩散电流基本可以忽略;不同有机材料的OTFT器件，电流大小有较大差异，这是因为不同有机材料中局域态之间的有效波函数重叠程度不同;OTFT的电流随温度升高明显增大，这是因为载流子服从变程跳跃拿输运理论，温度升高，导致载流子的长程跳跃加剧，因此电流增加.本模型相对简单，具有更高的精度，适用于电路模拟器.

［1］刘玉荣，左青云，彭俊彪，等.己基聚3-噻吩聚合物薄膜晶体管的稳定性［J］.华南理工大学学报:自然科学版，2010，38(5):65-70.Liu Yu-rong，Zuo Qing-yun，Peng Jun-biao，et al.Stability of polymer thin-film transistors based on poly(3-Hexylthiophene) ［J］.Journal of South China University of Technology:Natural Science Edition，2010，38(5):65-70.

［2］Horowitz G，Delannoy P.An analytical model for organicbased thin-film transistors［J］.Journal of Applied Physics，1991，70(1):469-475.

［3］Toris L，Dodabalapur A，Katz H E.An analytical model for short-channel organic thin-film transistors［J］.Journal of Applied Physics，1995，78(2):1088-1093.

［4］Necliudov P V，Shur M S，Gundlach D J，et al.Modeling of organic thin film transistors of different designs［J］.Journal of Applied Physics，2000，88(11):6594-6597.

［5］Calvetti E，Colalongo L，Kovacs-Vajina Z M.Organic thin film transistors:a DC/dynamic analytical model［J］.Solid-State Electronics，2005，49(4):567-577.

［6］Torricelli F，Kovacs-Vajina Z M，Colalongo L.A charge control analytical model for organic thin film transistors［J］.Applied Physics Letters，2008，92(11):113306-1-113306-3.

［7］Torricelli F，Kovacs-Vajina Z M，Colalongo L.A chargebased OTFT model for circuit simulation ［J］.IEEE Transactions on Electron Devices，2009，56(1):20-30.

［8］Marinov O，Deen M J，Zschieschang U，et al.Organic thinfilm transistors:part Ι—compact DC modeling ［J］.IEEE Transactions on Electron Devices，2009，56(12):2952-2961.

［9］Marinov O，Deen M J，Datars R.Compact modeling of charge carrier mobility in organic thin-film transistors［J］.Journal of Applied Physics，2009，106(6):064501-1-064501-13.

［10］Kalb W L，Batlogg B.Calculating the trap density of states in organic field-effect transistors from experiment:a comparison of different methods［J］.Physical Review B，2010，81(3):035327-1-035327-13.

［11］Arora N D.MOSFET models for VLSI circuit simulation［M］.New York:Springer-Verlag，1993.

［12］Shur M，Hack M.Physics of amorphous silicon based alloy field-effect transistors［J］.Journal of Applied Physics，1984，55(10):3831-3842.

［13］Chen T L，Gildenblat G.Analytical approximation for the MOSFET surface potential［J］.Solid-State Electronics，2001，45(2):335-339.

［14］Wu M W，Conwell E M.Transport in α-sexithiophene films［J］.Chemical Physics Letters，1997，266(3/4):363-367.

［15］Fadlallah M，Billiot G，Eccleston W，et al.DC/AC unified OTFT compact modeling and circuit design for RFID applications［J］.Solid-State Electronics，2007，51(7):1047-1051.

［16］Vissenberg M C J M，Matters M.Theory of the fieldeffect mobility in amorphous organic transistors［J］.Physical Review B，1998，57(20):12964-12967.