带宽自适应的Mean Shift目标跟踪算法*

王年 丁业兵 唐俊 鲍文霞

(安徽大学电子信息工程学院，安徽合肥230039)

运动目标跟踪广泛应用于智能人机交互、视频监控等，在生产生活、工程科学中有重要的研究价值.基于Mean Shift的目标跟踪算法具有实时性、鲁棒性.文献［1］中将Mean Shift算法应用于图像平滑和分割.文献［2］中将Mean Shift算法应用于人脸跟踪.文献［3-4］中将Mean Shift算法应用于目标跟踪领域，通过目标模型和候选模型间的Bhattacharyya系数来度量相似性，最终迭代至极值点.

基于Mean Shift的目标跟踪算法中，核函数带宽(即跟踪窗口大小)决定了参与迭代的样本数.在跟踪过程中，如果窗口大小始终不变，那么当目标存在明显的尺度变化时，就会导致跟踪产生偏差甚至使目标丢失，因此，自适应调整窗口大小具有重要的意义.文献［4］中对带宽进行±10%的增量修正，当Bhattacharyya系数最大时，确定当前帧的带宽，然而此相似性度量会在小窗口中达到局部最大，因此该方法适用于目标尺寸缩小的情况.文献［5］中基于尺度空间理论使目标跟踪的核函数带宽可以实时变化，但与文献［4］中方法有类似缺陷，而且计算量大.文献［6］中提出了一种基于后向跟踪、形心配准的核窗半径自动选取算法，但该算法要求运动目标的变化满足仿射模型，并需要进行形心配准和特征点对的回归计算.文献［7］中针对固有的小尺度游荡和尺度跟踪滞后问题，修改最优带宽判别条件，给出了自适应滤波器参数的设计方法.文献［8］中提出了一种改进的用于更新核函数带宽的SMD Shift算法.文献［9］中利用推导的核函数带宽自动选择公式进行目标尺度定位.文献［10］中采用跟踪窗口内协方差矩阵主分量分析法来计算目标方向和尺寸大小.文献［11］中根据尺度空间理论提出一种尺度方向自适应Mean Shift跟踪算法，此算法因计算量大而不能满足实时性要求，且复杂背景下的目标跟踪效果不理想.为此，文中提出了自适应调整核函数带宽的Mean Shift目标跟踪算法.首先利用目标特征概率投影来创建目标概率密度分布图，计算其零阶矩，再根据零阶矩值自适应调整核函数带宽，经矩运算后用椭圆来锁定目标.最后通过实验验证了算法的有效性和鲁棒性.

1 Mean Shift目标跟踪算法

在视频起始帧选取感兴趣目标进行初始化跟踪，设目标中心为 x0，像素值为 xi(i=1，2，…，n)，目标特征值为uj(j=1，2，…，m)，目标特征值基于核函数的概率密度为

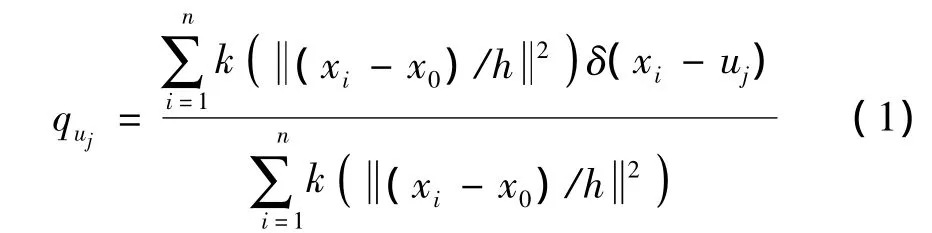
式中:h为核函数带宽;δ(xi－uj)用于判断目标区域中像素值xi是否属于特征值uj;k(x)为核函数K(x)的剖面函数，距离目标中心越近，像素权值越大.文中采用如下核函数:

假设当前帧以xc为中心，则候选目标特征值基于核函数的概率密度为

相似性函数给出了目标模型和候选模型间的相似程度.理想状况下两种模型的概率分布完全一样.目标跟踪转化为在当前帧寻找最优位置点，使得目标模型与候选模型的相似度最大.选择 Bhattacharyya系数来度量候选模型与目标模型的相似性，定义为

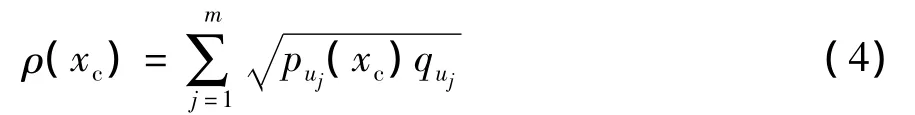
ρ(xc)值越大，模型的相似度越大.在当前帧中ρ(xc)取得最大的候选目标区域就是目标位置.设上一帧目标中心点为x0，将ρ(xc)在x0位置进行泰勒展开:

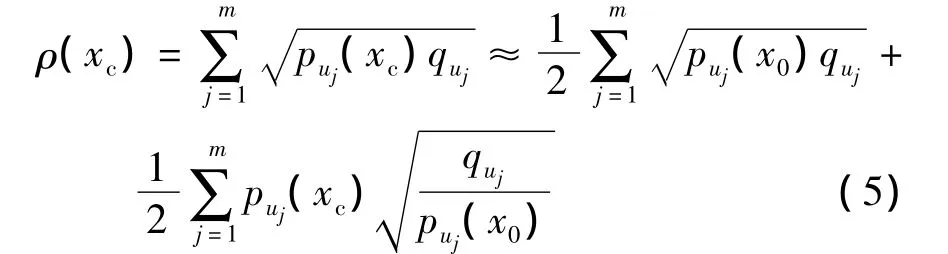
将式(3)代入式(5)，得

根据核函数密度梯度推导Mean Shift向量，当ρ(xc)取得最大值时，中心点xa为

式中，g(x)是k(x)的负导函数，即g(x)=－k'(x)，其对应的核函数G(x)=g(x2).

最后，通过Mean Shift算法不断迭代得到最优目标位置点.

2 改进的Mean Shift目标跟踪算法

2.1 目标概率密度分布

文中采用HSV颜色空间，Cam Shift算法使用HSV颜色空间的H分量创建直方图目标模型，建立目标概率密度分布图.Mean Shift目标跟踪算法将RGB颜色空间均匀剖分为16×16×16直方图区间［12］.由目标特征值概率在每帧最优位置区域投影创建概率密度分布图，并将分布点像素值转换为1～255之间.分布点特征值为

目标概率密度分布图确定了目标的几何形状特性，密度分布块随着目标大小、形状的变化而变化.

2.2 核函数带宽自适应调整

由Mean Shift算法迭代寻找到最优位置区域，然后计算该区域内的密度零阶矩 M00.I(x，y)为(x，y)位置处的概率密度估计值，x和y的变化范围为搜索窗区域.，窗口宽度为 s=，窗口长度 v=ts，t为初始化跟踪窗口长宽之比.因而核函数带宽h为

当目标丢失或完全遮挡后，调整搜索区域为整幅图像.

用椭圆锁定待跟踪目标，椭圆的长轴、短轴及方向角由零阶矩、一阶矩和二阶矩计算获得.一阶矩为

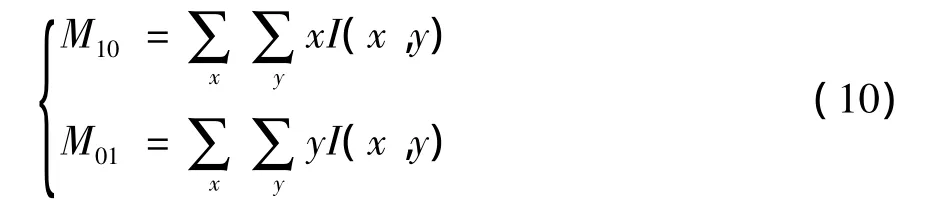
二阶矩为

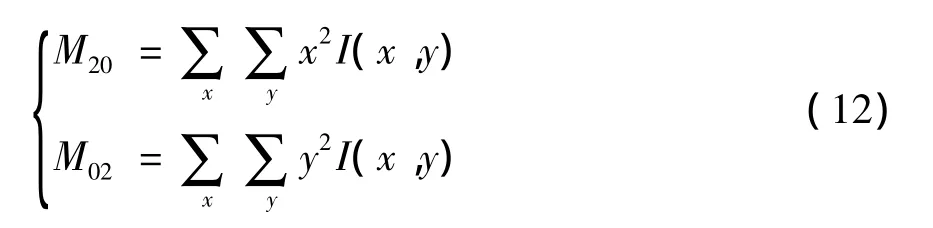
令a=M20/M00－¯x2，b=2(M11/M00－¯x¯y)，e=2(M02/M00－¯y2)，目标方向角θ为长轴与水平方向的夹角，θ=2－1arctan(b/(a－e))，长轴 l和短轴 d分别为

2.3 目标跟踪算法的步骤

带宽自适应调整的Mean Shift目标跟踪算法步骤如下:

1)初始化搜索窗口的大小和位置;

2)计算初始化窗口内目标特征的概率密度估计值;

3)以前一帧中心点x0为中心，计算候选目标特征概率密度估计值;

4)计算权重wi，根据式(7)估计目标的新位置中心点xa;

5)以新位置中心点xa为中心，更新候选目标特征值基于核函数的概率密度估计值;

7)由初始目标特征值概率在最优目标位置区域的投影创建概率密度分布图;

8)计算概率密度分布图零阶矩M00，调整搜索窗口大小，核函数带宽h随之更新，并计算椭圆长轴、短轴和方向角，锁定目标，转步骤3).

3 实验及结果分析

程序在Matlab编程环境下调试.人脸图像序列为人脸跟踪专用测试序列图像，大小为96×128，共500帧.初始化是在第一帧中手工完成的.

图1 两种算法对人脸图像序列的跟踪结果比较Fig.1 Comparison of tracking results for face image sequence using two algorithms

图1(a)给出了核函数带宽自适应调整算法在距离远近、转身、旋转、背景色干扰和外部人脸干扰下的目标人脸跟踪效果.典型的人脸目标跟踪帧图像第30～78帧的测试者由近及远，人脸窗口大小自适应调整;第80～122帧和第160～260帧的测试者转身侧对和背对摄像机，人脸并不失锁;第280～360帧有类肤色干扰，且人脸旋转，光照变化大，椭圆仍然能够准确锁定人脸，并随着人脸的旋转而相应偏转;第420～470帧中有另外一位测试者逐渐遮挡了被跟踪的人脸，椭圆仍能够准确锁定人脸.

图1(b)给出了传统Mean Shift目标跟踪算法［2］在相同环境下的跟踪结果.从图1可以看出:当目标逐渐缩小时，传统Mean Shift目标跟踪算法的跟踪结果较好，但当目标逐渐增大时，核函数带宽很难再扩大，因为相似性度量Bhattacharyya系数往往会在较小的跟踪窗口中达到局部最大;文中算法不仅能够准确跟踪目标，而且能够随着目标缩放、旋转自适应调整跟踪窗口的大小、方向.

图2给出了传统Mean Shift目标跟踪算法和文中算法的跟踪误差曲线.从图2中可见:文中算法的跟踪误差较传统Mean Shift目标跟踪算法小;统计误差近似呈高斯分布，故用其作为实验数据值与真实值之间误差的参考评估标准.表1给出了这两种算法的中心点x坐标、y坐标和核函数带宽的均值及标准差的统计误差值.从表1中可见，文中算法的跟踪效果较好.

下面分析两种算法的计算量.传统Mean Shift目标跟踪算法在每帧用3个不同大小的核函数带宽进行计算，取Bhattacharyya系数最大时对应的核函数带宽为最佳核函数带宽，比文中算法多3次Bhattacharyya系数、2次不同大小核窗内像素直方图的计算，使用了2次双循环运算.文中算法与传统Mean Shift目标跟踪算法相比，在每帧多计算了1次核窗内的概率密度分布，且计算了零阶矩、一阶矩和二阶矩，同样运用了2次双循环运算.所以理论上文中算法与传统Mean Shift目标跟踪算法的运算量基本相同.

Cam Shift算法使用HSV颜色模型中的H分量直方图投影创建概率密度分布图，通过计算概率密度分布质心来定位目标中心点.图3给出了Cam Shift算法与文中算法对类肤色干扰下的人脸图像序列的跟踪结果，由图3可以看出，整个跟踪过程中文中算法在类肤色干扰下仍能够稳定跟踪人脸，而Cam Shift算法则容易受到相似颜色影响而丢失目标.

图2 两种算法对人脸图像序列的跟踪误差曲线Fig.2 Tracking error curves for face image sequence using two algorithms

表1 文中算法与传统Mean Shift算法对人脸图像序列的跟踪误差比较Table 1 Comparison of tracking errors for face image sequence using the proposed algorithm and the traditional Mean Shift algorithm

图4显示了Cam Shift算法和文中算法的跟踪误差曲线.从图4中可见，文中算法的相对误差较小，跟踪效果更好.

图3 两种算法对类肤色干扰下的人脸图像序列的跟踪结果比较Fig.3 Comparison of tracking results for face image sequence in similar color using two algorithms

图4 文中算法和Cam Shift算法对类肤色干扰下的人脸图像序列的跟踪误差曲线Fig.4 Tracking error curves for face image sequence in similar color using the proposed algorithm and the Cam Shift algorithm

表2给出了两种算法的中心点坐标和核函数带宽的算术平均误差.从表2中可见，文中算法在相似颜色干扰和光照变化等复杂环境下的跟踪性能要优于Cam Shift算法.

表2 文中算法与Cam Shift算法对人脸图像序列的跟踪误差比较Table 2 Comparison of tracking errors for face image sequence using the proposed algorithm and the Cam Shift algorithm 像素

4 结语

核函数带宽在Mean Shift目标跟踪算法中起着至关重要的作用.文中通过计算最优目标位置区域概率密度零阶矩来自适应调整核函数带宽，并经矩运算用椭圆锁定实时变化的目标.人脸跟踪实验表明，文中算法不仅能够准确跟踪目标，而且能够随着目标缩放、旋转自适应地调整跟踪窗口的大小、方向.文中算法尤其适用于跟踪易于分割的分布块.

［1］Comaniciu D，Meer P.Mean Shift:a robust approach toward feature space analysis［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2002，24(5):603-619.

［2］Bradski G R.Real time face and object tracking as a component of a perceptual user interface［C］∥Proceedings of IEEE Workshop on Applications of Computer Vision.Berlin:IEEE，1998:214-219.

［3］Comaniciu D，Ramesh V，Meer P.Real-time tracking of non-rigid objects using Mean Shift［C］∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.SC Hilton Head Island:IEEE，2000:142-149.

［4］Comaniciu D，Ramesh V，Meer P.Kernel-based object tracking［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(5):564-577.

［5］Collins R T.Mean-Shift blob tracking through scale space［C］∥Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Los Alamitos:IEEE，2003:234-240.

［6］彭宁嵩，杨杰，刘志，等.Mean-Shift跟踪算法中核函数窗宽的自动选取［J］.软件学报，2005，16(9):1542-1550.Peng Ning-song，Yang Jie，Liu Zhi，et al.Automatic selection of kernel-bandwidth for Mean-Shift object tracking［J］.Journal of Software，2005，16(9):1542-1550.

［7］左军毅，梁彦，赵春晖，等.Mean Shift跟踪算法中尺度自适应策略的研究［J］.中国图象图形学报，2008，13(9):1750-1757.Zuo Jun-yi，Liang Yan，Zhao Chun-hui，et al.Researches on scale adaptation strategy in Mean Shift tracking algorithm ［J］.Journal of Image and Graphics，2008，13(9):1750-1757.

［8］Li Zhi-dong，Chen Jing，Schraudolph N N.An improved Mean-Shift tracker with kernel prediction and scale optimisation targeting for low-frame-rate video tracking［C］∥Proceedings of the 19th International Conference on Pattern Recognition.Florida Tampa:IEEE，2008:1-4.

［9］江焯林，黎绍发，贾西平，等.基于非参数聚类和多尺度图像的目标跟踪［J］.华南理工大学学报:自然科学版，2009，37(1):34-41.Jiang Zhuo-lin，Li Shao-fa，Jia Xi-ping，et al.Target tracking based on nonparam etric clustering and multi-scale images［J］.Journal of South China University of Technology:Natural Science Edition，2009，37(1):34-41.

［10］颜佳，吴敏渊，陈淑珍，等.跟踪窗口自适应的Mean Shift跟踪 ［J］.光学精密工程，2009，17(10):2606-2610.Yan Jia，Wu Min-yuan，Chen Shu-zhen，et al.Mean Shift tracking with adaptive tracking window ［J］.Optics and Precision Engineering，2009，17(10):2606-2610.

［11］张恒，李立春，于起峰.尺度方向自适应Mean Shift跟踪算法［J］.光学精密工程，2008，16(6):167-173.Zhang Heng，Li Li-chun，Yu Qi-feng.Scale and direction adaptive Mean Shift tracking algorithm ［J］.Optics and Precision Engineering，2008，16(6):167-173.

［12］李培华.一种改进的Mean Shift跟踪算法［J］.自动化学报，2007，33(4):347-354.Li Pei-hua.An improved Mean Shift algorithm for object tracking［J］.Acta Automatica Sinica，2007，33(4):347-354.