双半轴轴系结构的功率流传递特性

李秋红，薛开，李燕

(哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

测试转台被广泛应用在航天、航空工业，无论是作为飞行器仿真和惯性导航测试设备的试验平台，还是作为大型射电望远镜、天文望远镜、雷达天线、光电跟踪系统等设备的支承架，它都承担着设备的载体和控制系统的控制对象的双重角色.转台框架的结构形式通常为U型、O型、T型等，其中U型、O型在多轴结构中被广泛应用，半轴式结构支撑框架在这些结构形式中普遍存在.基于这类结构的特点和转台作为复杂机电耦合产品的特性，在实际工作中不可避免地存在不同幅度的振动.为了使转台系统安全可靠地工作，保证转台的高精度要求，因此需要对转台的振动特性进行研究.

目前，关于转台的动态特性问题，国内外学者做了大量工作，主要通过数值仿真来计算转台的动态特性，获取固有频率和模态振型等，以期在结构设计中避开共振［1-3］.关于转台振动研究不多，因为转台结构复杂，振动机理不容易解析.考虑到实际工作中复杂的机械结构、联接形式，导纳功率流法在描述有限子结构之间的振动能量传递有一定的优势，因为结构上任意一点的振动响应特性总可以用输入导纳或传递导纳来表示［4-6］，因此可以利用导纳功率流法来研究具有典型半轴式结构的转台振动机理.转台系统的振动主要来自驱动元件，要降低系统的振动，目前主要有以下几种策略:减小振源振动、改善减振装置、隔离机器设备［7］.若从减少振源的振动来说，成效不大，因振源主要来自于驱动元件的耦合振动，振动形式比较固定;改善减振装置、隔离设备，是目前较可行的方法.在无法减小振源的情况下，研究振动的能量传递路径及每一个子结构的能量损耗，并在此基础上采取隔振措施，显得尤为重要.

因此，本文在功率流研究的基础上，利用传递矩阵和子结构导纳法在理论上推导了各部分结构的振动功率流，通过实验对单轴转台振动功率流进行分析研究，利用功率流理论评价各传递路径上的振动能量传递规律，并分析了振动功率流经由各子结构的能量损耗，为振动机理研究提供了实验支持.

1 理论模型

具有U型、O型框架的半轴式转台结构的轴系，主要由驱动元件、2根半轴、轴承、框架、连接件、测角元件，测速机等组成.实际转台结构简化模型如图1所示.应用子结构分析方法，将其分为轴I子结构、轴II子结构、轴承I子结构、轴承II子结构、框架子结构、支架—底座子结构.其中振源为轴，经由路径轴承把振源与接受体连接起来，框架作为接受体1，支架和底座作为接受体2.振动能量传递过程是由力和力矩产生的激励，经由轴承传递到框架、支架—底座.

如图1所示的模型，系统受到一个来自轴端的复合激励，包括Y轴和Z轴方向上的扰动及绕X轴的力矩作用.

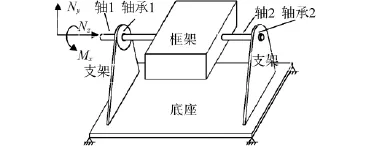
图1 单轴转台结构简化模型Fig.1 Model machine of meal-assistance robot

1.1 轴的传递特性

将轴划分为各个轴段，每段轴所受的扰动力和相应的速度响应为

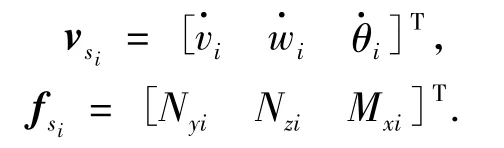
经过轴段传递速度响应为

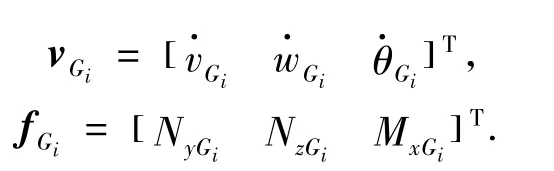
因为刚性轴有微小振动，由传递矩阵法可得［4］

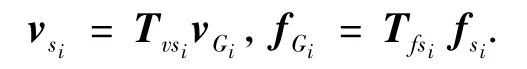
式中:

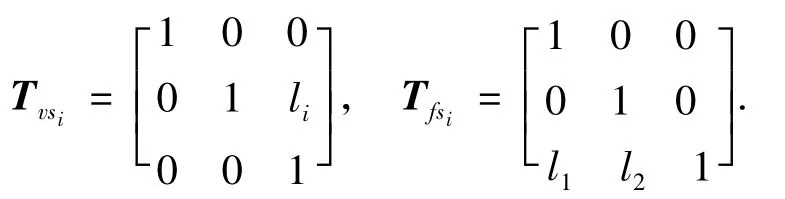
式中:l1、l2分别为轴段的长度和直径.

以轴I子结构为例，则根据动力学平衡准则可以得到如下方程:

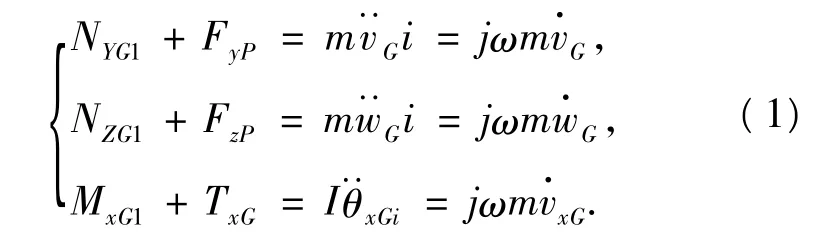
式中:FyP、FzP、TxP为振源激励，m 是轴段质量，IG是轴相对于X轴的转动惯量.初始激励表示如下:

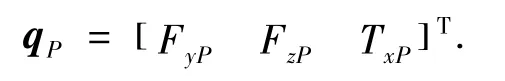
则式(1)整理为矩阵形式表示为

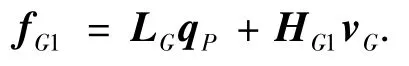
其中LG和HG表示为

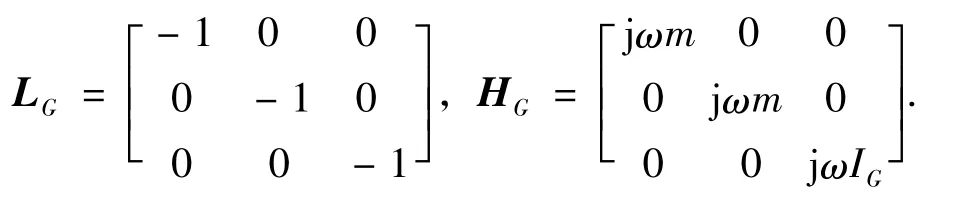
用导纳矩阵表示振源的动力学模型，速度和力矢量可表示为如下形式:

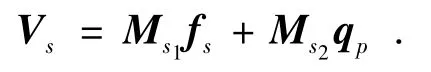
其中导纳矩阵由以上各式可得:

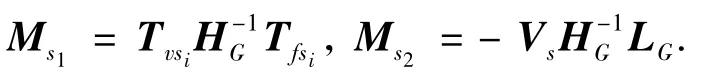
其余各轴段的传递特性可利用上述方法推导.

1.2 轴承的传递特性

轴承在本质上是一个多自由度耗散能量的传递路径，其动力学特性对系统的影响特别明显.将轴承的平移刚度和角刚度组集为如下形式:

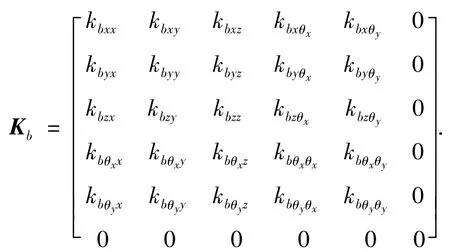
其中矩阵第6行和第6列为0，轴承矩阵沿对角线方向对称.这是因为本刚度矩阵基于轴承沿内圈Z轴转动，沿Z轴的旋转变形可以忽略，与其对应的刚度也可设为0，其他矩阵元素的具体计算参见文献［8］.

若考虑轴承阻尼Cb的影响，则滚动轴承的导纳［6］为

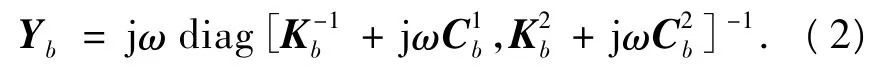
式中:Cb=ηKb;η为阻尼比例因子.

由轴承传递到支架—底座系统的力为

式中:Fbi表示轴承与支架连接处轴承对支架的作用力，Dbi轴承处的位移响应.

它们分别表示为

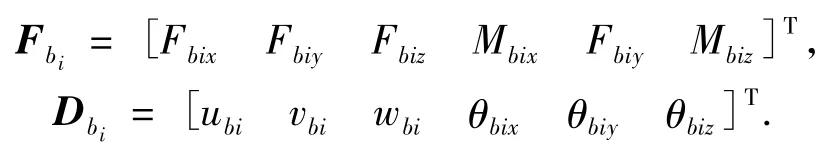
继而可求出输入轴承的功率流.

1.3 框架的传递特性

将2根半轴支撑的框架系统作为刚体看待，为简化模型，将2根半轴支撑的等效为两端简支的刚度板，其动态传递方程为

其中:

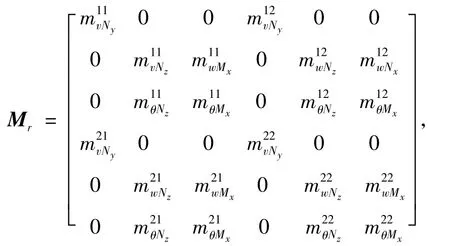
式中:mjj为连接点出的点导纳，mjk为连接点j和连接点k之间的传递导纳.

1.4 支架底座传递特性

支架和底座采用螺栓连接，为简化模型，把支架-底座作为整体，支架和底座都采用板式结构，轴承孔尺寸相对于支架底座较小，可将其看作一个板类结构的刚体，底座四边简支，得到刚体运动方程［10］式为

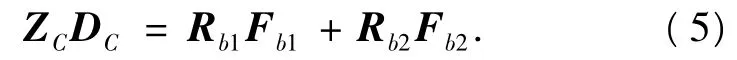
式中:ZC=-ω2MC，

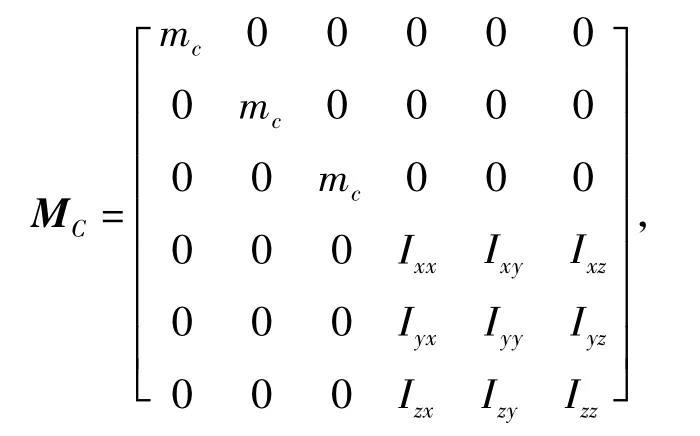
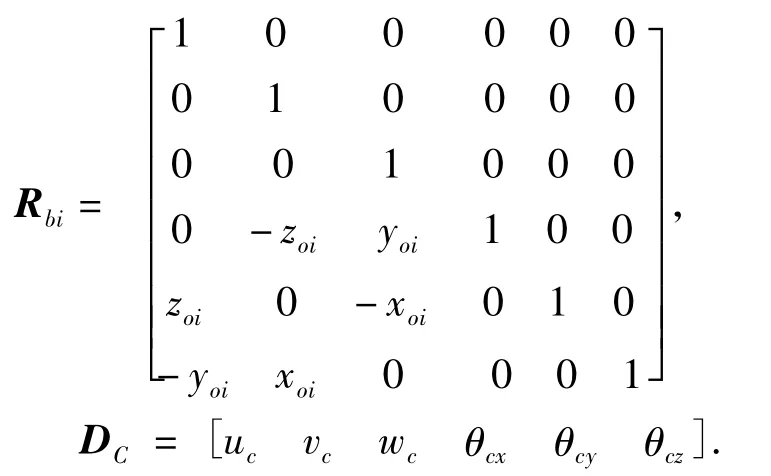
上述Zc为刚性支架-底座的位移阻抗;Rbi表示两轴承与支架-底座连接处到其质心在局部坐标变换矩阵;mc表示刚性支架-基础质量;Iij表示惯性矩Dc表示支架-底座质心位移响应，由刚体运动规律可求得

1.5 功率流计算

根据上述各部分结构的传递特性，可以求出传递到各部分子结构的响应，和各子结构的作用力，进一步对系统的功率流进行研究.

由振动功率流理论，在0～T时刻内的振动功率流［12］为

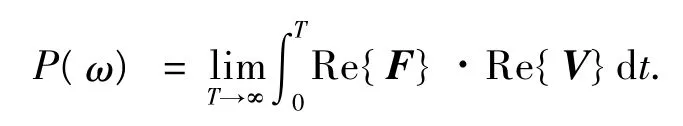
由轴端输入到系统的平均功率流为Ps1为

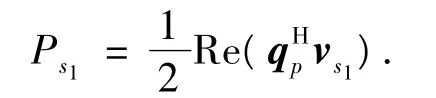
经由轴承传递到支承结构的功率流Pb为

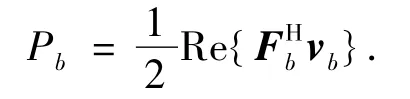
经过轴承传递到框架结构的功率流Pr为

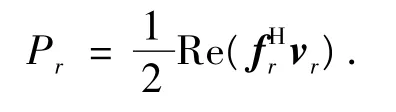
输入支架-底座的功率流Pc为

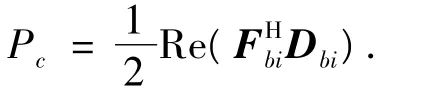
2 振动功率流传递实验研究

2.1 振动功率流实验与分析

实验中，在沿着系统轴端方向利用白噪声信号进行激振，以模拟电机的扰动.在激振点安装阻抗头，在各个子结构安装加速度传感器.速度信号由加速度传感器采集，力的信号由应变片来采集，通过转化变为应力，经过数据处理，获得功率流信息.经实验测得转台系统各部分的功率流如图2所示.图2(d)中的信号采样点为底座右侧点.

从图2可以看出，输入系统各部分的功率流，在低频时衰减很慢，随着激振频率的升高，衰减加快，频率越高，输入的功率流越小.由图2(c)、(d)可以看出中间框架结构对系统的功率流影响很大，从各频段的平均功率流的数值可明显看出，随着路径的增长，传递到、支架-底座上的功率流会明显减少，说明框架结构刚度增加时，会有效隔离振动的传递.特别值得注意的是，在低阶的某些频率处，传递到支架-底座的功率流甚至会大于传递到中间框架结构的功率流，这说明在框架、支架和底座共同的振动中，2个子结构的低阶模态发生了强烈的耦合.导致系统失稳，因此支架-底座的刚性对于系统的稳定性至关重要，提高支架-底座的结构刚度，有利于降低传输到支架-底座的功率流，同时可保证整个系统的稳定性.

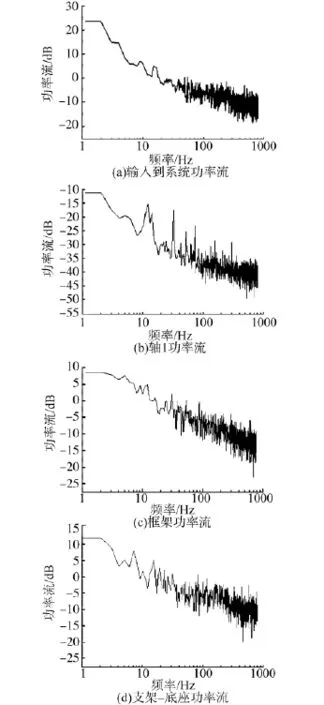
图2 转台系统的功率流Fig.2 The power of turntable system

2.2 振动传递路径分析

在轴承I处振动功率流分成2个传递路径.其中路径1为:振源—轴承I—轴I—框架左侧点—框架右侧点—轴II—轴承II—支架右—底座右;路径2为:振源—轴承I—支架左—底座左.分别在传递路径上选取适当的采样点，将由采样处获得力和速度响应，进行数据处理得到各处功率流.选取在不同耦合共振点的激振频率处的功率流进行对比分析，图3(a)为传递路径1上的功率流，图3(b)为传递路径2上的功率流.

从图3(a)中可以看出在路径1上，经过轴承能量损耗比较明显，在不同频率处衰减率不同，且在高于600Hz以上激振频率随着数值的增加而显著变大，因此合理的轴承的建模对于系统优化至关重要.从图3(a)中的采样点5在低频段的功率流均高于采样点4，由此可以看出这类半轴式结构，因其存在闭环结构特点，在框架右侧存在严重振动耦合.同理采样点8处也存在相类似情况.从图3(b)中可以看出经由轴承处后能量变化不是非常明显，主要是因为传递路径短，振动能量随着路径的加长而规律地衰减.

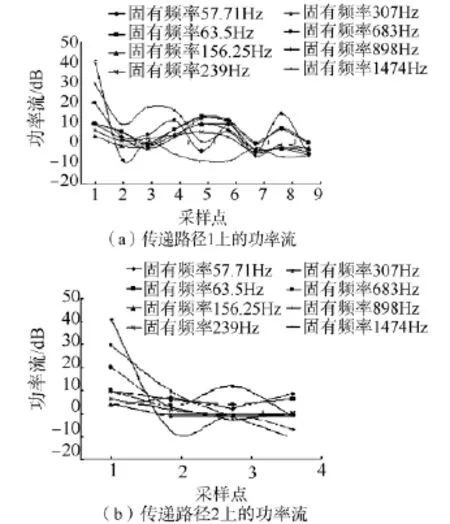
图3 传递路径上的功率流Fig.3 The power of transmission path

3 结论

本文对单轴转台进行了动力学分析和功率流测试实验研究，得到以下结论:

1)双半轴转台结构的功率流分布的规律为:输入系统各部分的功率流随着激振频率的升高衰减幅度也随之加快;输入到基础的平均功率流随着传递路径的增加而减少，表明框架的结构刚度能有效地隔离振动.

2)双半轴式转台其闭环结构的特点使得支架-底座和框架2个子结构在低阶模态发生了强烈的耦合，导致系统失稳，因此提高支架-底座的结构刚度，可有效地保证整个系统的稳定性.

3)采用振动传递路径分析方法，能有效地分析存在多条传递路径结构的功率流传递特性，根据各传递路径的振动能量分布特点，采取相应减振措施，能获得良好减振效果.

［1］LIU Qiaosheng，XI Juntong.Case-based parametric design system for test turntable［J］.Expert Systems with Applications，2011，38:6508-6516.

［2］李杰.精密光电跟踪转台框架的静动态特性分析［J］.光电工程，2010，37(1):61-64.LI Jie.Static and dynamic analysis of the precision opto-electronic tracking turntable frame［J］.Opto-Electronic Engineering，2010，37(1):61-64.

［3］耿雷，季旭，李海越.三轴转台结构静动态特性分析［J］.组合机床与自动化加工技术，2008，4:1-4.GENG Lei，JI Xu，LI Haiyue.Static and dynamic characteristics of three-axis turntable［J］.Modular Machine Tool＆ Automatic Manufacturing Technique，2008，4:1-4.

［4］GARDONIO P，ELLIOTT S J，PININGTON R J.Active isolation of structural vibration on a multiple-degree-of-freedom system，part I:dynamics of the system［J］.Journal of Sound and Vibration，1997，207(1):61-73.

［5］XIONG Y P.Power flow analysis of complex coupled systems by progressive approaches［J］.Journal of Sound and vibration，2001，239(2):275-295.

［6］苏尔敦，王敏庆.梁板耦合结构振动功率流特性研究［J］.噪声与控制研究，2009，4:6-9.SU Erdun，WANG Meiqing.Study on vibration power flow characteristics of girder-plate coupled structures［J］.Noise and Vibration Control，2009，4:6-9.

［7］冯国平，谌勇，黄修长，等.基于功率流的柔性系统振动传递分析［J］.机械强度，2010，32(5):719-722.FENG Guoping，CHEN Yong，HUANG Xiuchang，et al.Based on the power flow of the flexible system transferring analysis［J］.Mechanical Strength，2010，32(5):719-722.

［8］LIM T C，SINGH R.Vibration transmission through rolling element bearings，part I:bearing stiffness formulation［J］.Journal of Sound and Vibration，1990，139(2):179-199.

［9］SUN L，LEUNG A Y T，LEE Y Y，et al.Vibrational powerflow analysis of a MIMO system using the transmission matrix approach［J］.Mechanical Systems and Signal Processing，2007(21):365-388.

［10］ROOK T E，SINGH R.Mobility analysis of structure-borne noise power flow trough bearings in gearbox-like structures［J］.Noise Control Eng J，1996，44(2):69-78.

［11］宋孔杰，李新德，闫鹏.齿轮传递系统振动功率流特性研究［J］.应用力学学报，2003，20(4):93-96.SONG Kongjie，LI Xinde，YAN Peng.Gear transmission system vibration power flow characteristics research［J］.Chinese Journal of Applied Mechanics，2003，20(4):93-96.

［12］牛军川，田国会，宋孔杰.旋转机械主动隔振研究I:功率流传递特性研究［J］.应用力学学报，2001，31(4):301-305.NIU Junchuan，TIAN Guohui，SONG Kongjie.Study on active isolation vibration part I:transmission property of power flow［J］.Chinese Journal of Applied Mechanics，2001，31(4):301-305.