改进粒子群算法在梯级水电站优化调度研究中的应用
2011-06-21吴月秋纪昌明郑江涛
吴月秋,纪昌明,郑江涛
(华北电力大学可再生能源学院新能源与可再生能源北京市重点实验室,北京102206)
改进粒子群算法在梯级水电站优化调度研究中的应用
吴月秋,纪昌明,郑江涛
(华北电力大学可再生能源学院新能源与可再生能源北京市重点实验室,北京102206)
The National Natural Science Foundation of China(51179069);The National Natural Science Foundation of China(51179130)。
梯级水电站水库优化调度是电力系统运行中的重要内容,各水电站之间既有水力联系,又有电力联系,比单一水库优化调度更为复杂,具有多维、动态、非线性等特点。目前国内外学者对梯级水电站水库优化调度常用的优化方法有动态规划法(DP)[1]、逐步优化算法[2]、遗传算法[3]等,各有其优点,但也存在明显的不足。用DP法求解时,随着水库数目的增加、优化时段的细分和离散点数的增加,计算速度会明显下降,出现“维数灾”;若水库多于2座,则逐步优化算法占用计算机内存随之增大,计算速度大大降低;遗传算法在处理复杂目标函数时具有独到的优势,但在处理众多约束条件和收敛速度上还存在问题。
粒子群优化算法(简称 PSO)是由美国的James Kennedy和Russell Eberhart于1995年最先提出的,算法源于对鸟群觅食行为的研究,通过对“鸟群”简单社会系统进行模拟,在多维解空间中构造具有一定规模的“微粒群”,并以微粒对解空间中的最优微粒的追随进行解空间的寻优搜索[4-5]。PSO提供了解决复杂问题的框架,结构简单,容易实现,且搜索速度快,近年来也有人把其用于水库调度中,并取得了一定的成果。但是,它缺乏有效的局部搜索机制,对复杂问题易早熟收敛,陷入局部极值点[6],从而影响了在水库优化调度中的广泛应用。
本文采用以随机动态改变惯性权重机制来选取惯性权重因子、以混沌变量生成机制增加粒子的多样性、以逐步优化和随机生成相结合增加粒子生成的有效性的改进粒子群算法(IPSO)进行求解。针对梯级水电站优化调度问题,建立了IPSO模型,并给出了具体的求解步骤。实例计算表明,该算法具有计算速度快,收敛性好的特点,为求解梯级电站优化调度问题提供了一种有效的方法。
1 梯级电站优化调度数学模型
给定控制期内径流过程中,在满足综合利用要求及其他约束条件下,以梯级发电量最大和保证出力最大为目标函数,建立梯级水电站联合调度的多目标优化数学模型。
1.1 目标函数
1)发电量最大目标函数。水电站发电通过电网向用户供电,从而产生发电效益。在水电站长期控制问题中,发电效益可直接由发电量大小计算,因而优化调度目标函数可以描述为:给定控制期内径流过程,在满足约束条件下使控制内梯级总发电量最大。即为

式中,Nt为t时段系统的总出力;Δt为系统的时段出力;T为计算期的总时段数。
2)保证出力最大目标函数。要使保证出力最大,就是使设计枯水段水电站群的最小时段出力最大,即为

式中,Nt为t时段系统的总出力;T为计算期的总时段数。
1.2 约束条件
1)水量平衡方程。
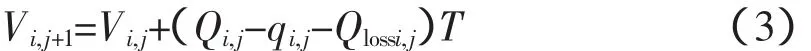
式中,Vi,j表示第j时段初第i电站蓄水量;Vi,j+1表示第j时段末第i电站蓄水量;Qi,j表示第j时段第i电站来流量;qi,j表示第j时段第i电站泄流量;Qlossi,j表示第j时段第i电站扣损流量;T表示月时段长度。
2)水库蓄水量限制。

式中,Vmindi表示第i电站的最小库容,一般是指死水位对应的库容;Vmaxsi表示第i电站的最大库容,一般是指正常蓄水位对应的库容,汛期可以是防洪限制库容。
3)水库下泄流量限制。

4)水电站预想出力限制。

式中,Nmax(Hi,j)表示第i电站第j时段的预想出力;Hi,j为第i电站第j时段发电水头。
5)边界条件约束。年调节水库从死水位开始计算,多年调节水库从死水位与正常高水位的1/3处起算。
1.3 模型的求解
对于多目标模型,本文通过将保证出力最大目标变化为约束条件,将多目标模型转化为单目标优化模型,进行优化计算。转化后的目标函数为
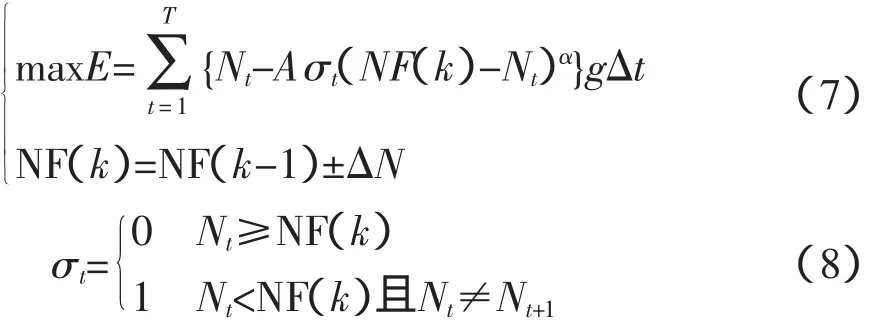
式中,NF(k)为第k次计算的梯级保证出力;Nt为t时段系统的总出力;Δt为系统的时段出力;A,α为惩罚因子;T为计算期的总时段数;ΔN为保证出力的搜索步长。
对于惩罚因子A,α,可通过调整它们的大小,来调整保证率的高低,使其与实际值相符;关于惩罚因子A,α对保证率的影响,可参考文献[7]。
本文对模型的求解采用改进粒子群算法,对方法的介绍和具体的求解如下。
2 IPSO算法
2.1 粒子群优化算法
PSO是一种基于群体的优化算法,群体中每个粒子表示问题的一个可行解,解的优劣由适应度函数决定。粒子在搜索空间中以一定的速度飞行,并根据自身的飞行经验以及当前最优粒子的状态对速度进行动态调整,个体之间通过协作与竞争,实现对问题最优解的搜索。
设在一个D维的搜索空间中,由m个粒子组成种群x={x1,x2,…,xi,…,xm},其中第i个粒子在D维搜索空间中的位置表示为向量xi=(xi1,xi2,…,xiD)T,其“飞翔”速度表示为vi=(vi1,vi2,…,viD)T。在每一次迭代中,粒子i通过跟踪2个“极值”来更新自己,一个是粒子i自身所经历的最好位置,记作pi=(pi1,pi2,…,piD)T,另一个是整个粒子群经历的最好位置,记作pg=(pg1,pg2,…,pgD)T,粒子i将按式(6)、式(7)改变速度和位置。

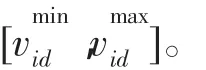
式(9)主要通过三部分来更新粒子i的速度:粒子i前一时刻的速度;粒子i的当前位置与其最好位置之间的距离;粒子i的当前位置与群体最好位置之间的距离。
2.2 算法的改进
粒子群算法在搜索后期粒子容易出现停滞现象,而陷入局部最优,加入混沌搜索机制就可以增加粒子的多样性,从而搜索到全局最优解。加入混沌搜索机制的思想实质就是当粒子在寻优的过程中,连续多次迭代的值都不发生变化时,即认为粒子出现停滞,从而对粒子生成混沌点列,重新开始搜索。
混沌是存在于非线性系统中的一种较为普遍的现象,在一定范围内混沌变量的变化具有随机性、遍历性和规律性[9]。利用混沌变量的这些特征进行优化搜索,可保持群体多样性,使算法跳出局部最优,从而改善算法的全局搜优性能。
粒子i生成混沌点列的步骤如下:
1)将粒子所在位置xi的每一维xid,d=1,2,…,D,按式(11)映射到区间[0,1]上

式中,[ad,bd]为第d维变量xid的定义域。


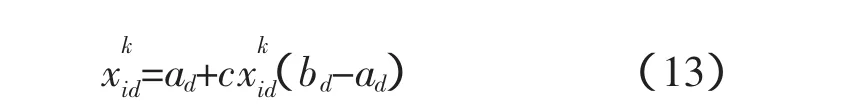
2.3 IPSO算法的设计
IPSO算法步骤如下。
步骤1:参数和种群的初始化。设定加速常数c1和c2,惯性权重ω,最大进化迭代数T,粒子群规模m,混沌映射迭代次数M。置当前进化代数t=1,在约束条件允许的范围内,随机初始化m个粒子。
步骤2:计算出每个粒子的适应度Ei,更新个体历史最优适应度Ep和全局最优适应度Eg,并根据粒子群当前的状态更新每个粒子的pbest和种群的gbest。
步骤3:判断每个粒子是否处于寻优滞留状态(局部最优)。如果连续n次迭代计算所得的ΔEi(ΔEi=(Ei-Ep)/Ei)都小于φ(φ为预先设定的常数阈值),则转入步骤4;否则粒子处于滞留状态。
1)按照2.2中的方法对粒子生成混沌点列;
2)计算所生成的每个点列的适应度,并更新粒子的最优适应度和最优位置;
3)判断是否达到迭代终止条件(最大迭代次数或收敛控制精度),如是则转至第4)步,否则转至第1)步,重新生成混沌点列;
4)用这个最优位置替代粒子原有的位置,速度保持不变。
步骤4:根据式(9)和式(10),更新每个微粒的位置和飞行的速度。
步骤5:判断是否达到迭代终止准则(最大迭代次数或收敛控制精度),如是,输出计算结果;否则,转至步骤2继续进行迭代计算。
改进粒子群算法的计算流程图如图1所示(虚线框中内容为混沌变量生成部分)。
4)由此可以得到xi经过Tent映射后的混沌点列:
2.4 IPSO算法在梯级电站优化调度中的应用
在利用IPSO算法对梯级电站优化调度问题的研究中,粒子在空间中的位置实际上代表着每个水库时段末水位值,其求解的过程也就是不断调整水位值,逐步逼近最优解,但需要注意以下几个问题。
2.4.1 粒子群的初始化
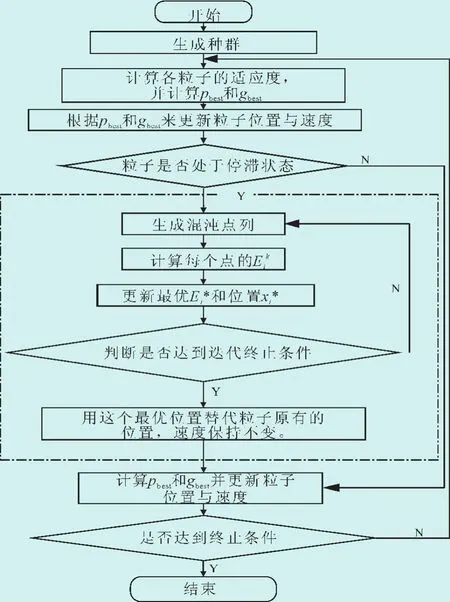
图1 IPSO流程图Fig.1 IPSO flow chart
初始种群的好坏对算法的搜优性能起很大的作用,初始种群生成的好,则算法搜寻全局最优解的能力就较强,反之则搜优效率较低。
对于梯级电站优化调度,本文采用与确定性优化方法——逐步优化方法(简称POA法)相结合的方法来生成初始种群,以增加生成粒子的有效性和算法搜优的性能。
粒子群算法初始种群生成步骤。
步骤1:运用POA法先进行求解,得到一组解,并将此解作为初始解;
步骤2:在初始解的基础上施加随机扰动,生成新的解,只对位置向量施加扰动。定义扰动公式如下

速度生成公式如下
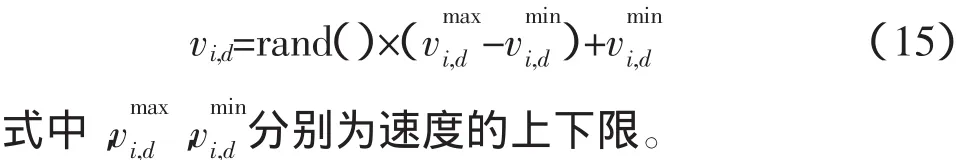
步骤3:用约束条件对位置向量进行检验,看是否满足约束条件,如满足则对确定下来的解再进行扰动,生成新的解,如不满足则返回步骤2,重新生成位置向量。
步骤4:直到生成m个满足条件的粒子结束。
2.4.2 适应度函数的确定
粒子的适应值是衡量粒子飞行位置优劣的惟一指标,也是实现粒子由初始位置不断“被吸引”到最佳位置的动力。结合梯级发电量最大和系统保证出力最大这一多目标模型,以目标式(7)作为微粒群的适应度函数。这样,每个粒子每到达一个新的位置,根据其在多维解空间上的坐标,就可以通过目标函数计算粒子在该位置上的适应值大小。然后,以此适应值与自身飞行得来的个体极值pbest点、群体飞行过程的全局极值gbest点之间的差距,动态地调整粒子飞行的速度,使之趋向全局最佳点,从而得到最优解。
2.4.3 约束条件的处理
梯级优化调度是一个典型的多约束优化问题,对于直接对应求解目标的状态变量(库水位或库容),由于微粒在多维空间中的位置代表的便是问题的解,因此可以直接通过对微粒位置的取值范围进行限定来实现约束;其他约束条件可通过罚函数的形式进行处理。对于惩罚函数的选取采用变量惩罚函数法[11],公式为
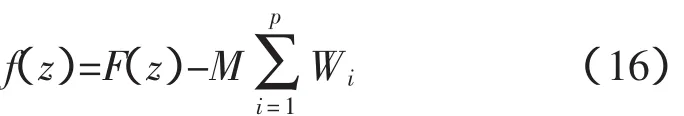
式中,F(z)为原优化问题的目标函数值;M为与进化代数有关的惩罚因子;Wi为与第i个约束有关的违约值;p为违约数目。
当约束条件多时,可能会出现使用罚函数效果不好的情况,此时惩罚项只取对适应度值影响较大的约束。例如,在水库调度中只对出力的限制作出惩罚,而其他的约束则要求必须满足,不满足时则舍弃该解。
3 优化结果的分析
为验证算法的可行性和有效性,以某梯级水电站的优化调度问题进行计算。其中微粒规模为30(经试算本实例微粒规模取30最合适),进化迭代次数取100,混沌迭代次数取200,计算ω时取ωmax=0.9,ωmin=0.4,学习因子c1=c2=2。
该梯级水电站包含两级水电站,两级水电站都具有年调节性能;两电站有区间入流汇入。两电站的死水位分别为350m和160m,调度期内控制最高限制水位分别为400m和200m;一级电站的装机容量为184万kW,最大过流能力为1300m3/s;二级电站装机容量为121.2万kW,最大过流能力为2130m3/s;已知两水库的水位-库容关系曲线、下游水位-流量关系曲线。
将水库优化调度时刻按月划分为12时段,初始水位取为361.8m和170.0m,采用C++语言编程,对两电站进行优化调度计算,优化后的结果见表1和图2;IPSO算法和PSO算法的优化结果对比见表2;图3为IPSO算法所得的2个电站的月末下泄流量过程。
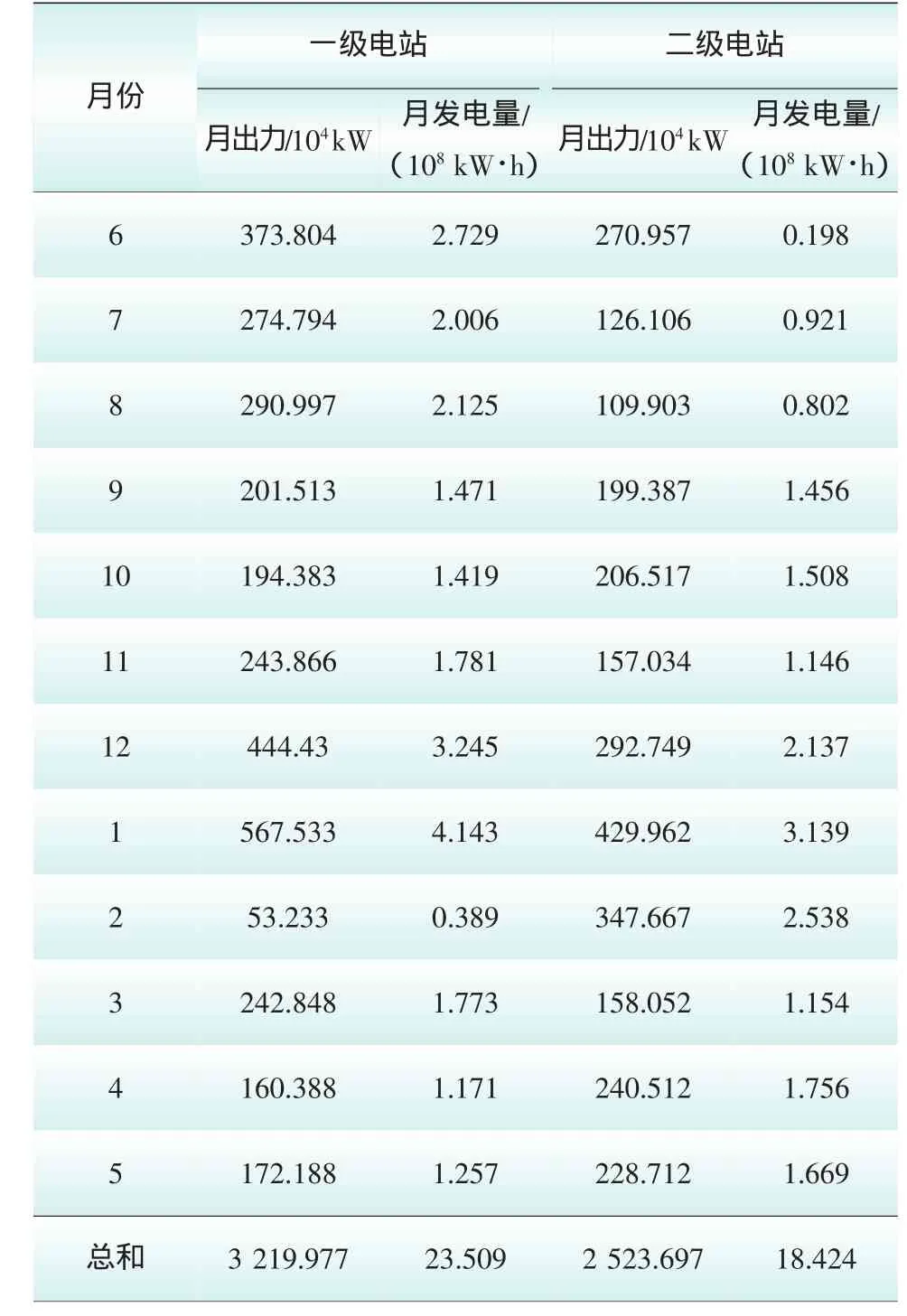
表1 IPSO算法计算结果Tab.1 Result of IPSO
从图2中可以看出,A电站和B电站自6月份开始到次年的1月份都在相对较高的水位运行,而此后均以相对较低的水位运行,这主要是因为到次年1月份此梯级电站来水开始减少,而6月份到次年1月份的蓄水正是为了充分利用汛期来水,减少弃水;这既提高了水量利用率,又增加了枯期发电量。由此可见,IPSO法算得的水位控制符合梯级电站优化调度的规律,计算结果合理可行。

图2 各电站时段末水位过程图Fig.2 The end of the period of the two hydropower stations water level process map
通过表1和表2可以看出,IPSO法得到的系统保证出力和发电量比PSO法和POA法得到的都要大,经济效益显著。从图3和表1可以看出,IPSO法能很快收敛于最优解,收敛性能好,解决了动态规划法的“维数灾”问题。
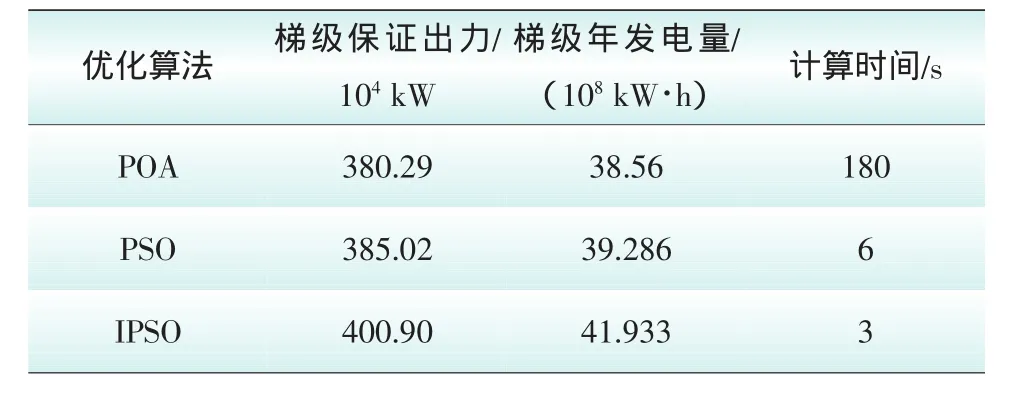
表2 优化调度结果对比Tab.2 Comparison of optimal results
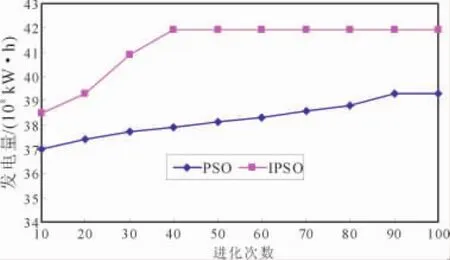
图3 发电量随进化次数的变化Fig.3 Generated energy changes with the number of evolution
4 结论
粒子群算法作为一种新兴的优化方法,为解决很多传统方法所难以解决的问题提供了新的思路,特别适用于水库优化调度。但传统粒子群算法具有易早熟和陷入局部最优的缺点,针对这种问题,本文将混沌搜索机制引入到粒子群算法中,并采用随机动态改变惯性权重机制来选取惯性权重因子,利用逐步优化方法生成初始种群。将混沌搜索引入到粒子群优化算法中,可以利用混沌的遍历性,增加了粒子群的多样性,较好地克服了粒子群算法的易早熟和陷入局部最优的缺点,从而获得了较好的收敛速度和计算精度。通过实例证明,把IPSO算法应用到梯级电站优化调度中,可以较好解决梯级电站调度中的多维强约束、多阶段、非线性的组合问题,为梯级电站优化调度提供了一种有效的方法。
[1]BELLMAN R.Dynamic Programming[M].New Jersey:Princeton University Press,1957:3-59.
[2]宗航,周建中,张勇传.POA改进算法在梯级电站优化调度中的研究和应用[J].计算机工程,2003,29(17):105-109.
ZONG Hang,ZHOU Jian-zhong,ZHANG Yong-chuan.Research and Application for Cascaded Hydroelectric Optimized Scheduling Based on Modified Adaptive POA[J].Computer Engineering,2003,29(17):105-109.
[3]涂启玉,梅亚东.遗传算法在水库(群)优化调度研究中的应用综述[J].水电站自动化与大坝监测,2008,32(1):16-18.
TU Qi-yu,MEI Ya-dong.Review on the Application of GeneticAlgorithmtoReservoir(s)OptimalOperation[J].Hydropower Automation and Dam Monitoring,2008,32(1):16-18.
[4]KENNEDY J,EBERHART R C.Particle Swarm Optimization[C]//Proc IEEE International Conference on Neural Networks.Perth,Australia,1995:1942-1948.
[5]KENNEDY J,EBERHART R C.A New Optimizer Using Particle Swarm Theory[C]//Proc of the Sixth International Symposium on Micro Machine and Human Science.Nagoya,Japan,1995:39-43.
[6]李安强,王丽萍,李崇浩,等.基于免疫粒子群优化算法的梯级水电厂间负荷优化分配[J].水力发电学报,2007,26(5):15-20.LI An-qiang,WANG Li-ping,LI Chong-hao,et al.The Optimized Loading Distribution Among Cascaded Hydropower Stations Based on Immune Particle Swarm Optimization Algorithm[J].Journal of Hydroelectric Engineering,2007,26(5):15-20.
[7]陈洋波,胡嘉琪.隔河岩和高坝洲梯级水电站水库联合调度方案研究[J].水利学报,2004(3):47-59.
CHEN Yang-bo,HU Jia-qi.Study on Integrated Operation of Cascade Hydropower Stations[J].Journal of Hydraulic Engineering,2004(3):47-59.
[8]李宁,付国江,库少平,等.粒子群优化算法的发展与展望[J].武汉理工大学学报,2005,27(2):26-29.
LI Ning,FU Guo-jang,KU Shao-ping,et al.Development and Prospect of a Particle Swarm Optimization Algorithm[J].Journal of Wuhan Automotive Polytechnic University,2005,27(2):26-29.
[9]李兵,蒋慰孙.混沌优化方法及其应用[J].控制理论与应用,1997,14(4):613-615.
LI Bing,JIANG Wei-sun.Chaos Optimization Method and Its Application[J].Control Theory and Applications,1997,14(4):613-615.
[10]单梁,强浩,李军,等.基于Tent映射的混沌优化算法[J].控制与决策,2005,12(2):179-182.
SHAN Liang,QIANG Hao,LI Jun,et al.Chaotic Optimization Algorithm Based on Tent Map[J].Control and Decision,2005,12(2):179-182.
[11]王少波,解建仓,孔珂.自适应遗传算法在水库优化调度中的应用[J].水利学报,2006,37(4):480-485.
WANG Shao-bo,XIE Jian-cang,KONG Ke.Application of Adaptive Genetic Algorithm in Optimization of Reservoir Operation[J].Journal of Hydraulic Engineering,2006,37(4):480-485.
Application of Improved Particle Swarm Algorithm in Optimal Scheduling of Cascade Hydropower Stations
WU Yue-qiu,JI Chang-ming,ZHENG Jiang-tao
(The New and Renewable Energy of Beijing Key Laboratory,School of Renewable Energy,North China Electric Power University,Beijing 102206,China)
In order to solve multi-dimensional,dynamic,nonlinearand otherdifficultproblems ofthe cascaded hydroelectric optimized scheduling,this paper adopts improved particle swarm optimization(PSO).To avoid the local optimization and prematurity of the PSO algorithm,the generation mechanism of chaotic variables are introduced to increase the diversity of particles,and the method of combing gradual optimization and random generation is used to generate the initial population to increase the effectiveness of particle generation.A study case of cascade reservoirs shows that better results can be achieved with the improved PSO.Therefore,it provides a new and efficient method for Cascade Hydropower Station operation scheduling.
cascade hydropower stations; optimal scheduling;improved particle swarm algorithm
针对梯级电站优化调度具有多阶段、非线性和组合性的特点,采用改进粒子群算法来求解。针对目前采用的基本粒子群算法在求解时存在易陷入局部最优和早熟的缺点,改进粒子群算法以混沌变量生成机制来增加种群的多样性,以逐步优化和随机生成相结合的方法生成初始种群,以增加粒子生成的有效性。实例计算结果表明,改进粒子群算法可以取得较好的效果,并为梯级电站优化调度提供了一种有效的方法。
梯级水电站;优化调度;改进粒子群算法
国家自然科学基金项目(51179069);国家自然科学基金项目(51179130)。
1674-3814(2011)12-0038-07
T V 697
A
2011-10-28。
吴月秋(1982—),女,助理工程师,主要从事水资源开发利用方面的研究。
(编辑 冯露)
