配电网络重构算法综述
2011-06-21李飞邱正美马丽朱铁铭
李飞,邱正美,马丽,朱铁铭
(1.临汾供电公司,山西 临汾 041000;2.潍坊供电公司,山东潍坊 261000;3.中国电力科学研究院,北京100192;4.萧山供电局,浙江 杭州 311201)
配电网络重构算法综述
李飞1,邱正美2,马丽3,朱铁铭4
(1.临汾供电公司,山西 临汾 041000;2.潍坊供电公司,山东潍坊 261000;
3.中国电力科学研究院,北京100192;4.萧山供电局,浙江 杭州 311201)
配电网络是闭环设计的,运行时则呈开环辐射状。这种辐射状结构相对网状结构具有很多优点,如短路电流小,开断电流和保护控制简单易行,但是整体的可靠性较低[1]。配电系统中存在大量的联络开关和分段开关,这两类开关主要作用是为进行故障隔离、供电恢复和对系统进行结构优化。系统发生故障时,一些分段开关将打开隔离故障支路,同时一些联络开关闭合将部分隔离或全部隔离后的支路转移到其他馈线或同一馈线的其余分支上;正常运行时,则通过两类开关的再组合来提高系统的可靠性和减少网损等[2]。
国外对于配电网络重构的研究较早,开始时主要针对城市配电网。城市配电网的特点是地下电缆使用较广泛,设计为环形结构而通常在辐射形结构下运行。农村配电网中主要使用架空线路,最初系统设计为辐射形,为了提高供电可靠性,不断增加分段开关和联络开关的数目,为电网重构提供了有利的条件。在我国,随着电网改造和配电管理系统(DMS)研发工作的蓬勃开展,配电网重构作为配电管理系统的重要功能之一,也逐渐开始得到广泛研究[3]。
1 配电网重构问题描述
配电网重构是在保证网络拓扑结构,满足线路热容、电压质量和变压器容量等要求的前提下,确定使配电网某一指标最佳的配电网运行方式[4]。
1.1 目标函数
1)系统有功网损最小。

式中,Ri,Pi,Qi,Ui分别表示配电网中第i条支路的电阻、有功功率、无功功率和母线电压。目前,很多关于配电网重构的文献都以有功网损最小为优化目标,如文献[5]等。实际配电系统中的潮流分布在时刻变化,优化时选择特定时间段内一个有代表性的状态,比如系统负荷最大的时刻,在此状态下进行配电网重构。
2)系统负荷分布均匀。


式中,li表示第i条支路的负荷平衡指数,即支路负荷和网络最大支路负荷的比值。电网建设速度不能满足负荷的增长速度,就会造成系统中的负荷不平衡,导致系统的能量损耗增加,系统过负荷的危险增加,线路长期超载运行会缩短使用年限,造成经济损失。
3)系统可靠性提高。
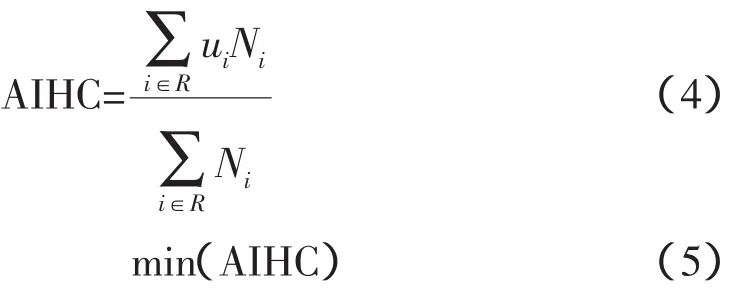
式中,ui为负荷点i的平均停运时间;Ni为负荷点i的用户数;R为系统中的负荷点集合。AIHC(Average Interruption Hours of Customer)是我国供电系统常用的可靠性指标之一,即用户平均停电时间。配网重构的实现,可以减少用户停电次数和平均停电时间,提高对用户的供电质量,同时也会减少系统网损。
4)给定时间段内系统能量损耗最小。

式中,Ri,Pi,Qi,Ui分别表示配电网中第i条支路的电阻、有功功率、无功功率和母线电压;λ1为单位能量损耗的费用系数;Ck为第k个开关在时间T内的投切费用;s代表时间T内系统状态发生改变的所有开关。为了降低计算的复杂性,采用阶梯型的负荷曲线代替实际连续的负荷曲线,即不考虑较小时间内的负荷波动。
5)电压水平提高。

系统母线电压过低会影响用户用电和电机的正常运行,配电网重构目标的实现可以维持母线电压水平,减少对用户的不良影响。
1.2 约束条件
1.2.1 潮流约束
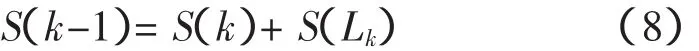
式中,S(k-1)为首端母线的注入功率;S(k)为末端母线的注入功率;S(Lk)为末端母线的负荷,如图1所示。

图1 系统功率关系示意图Fig.1 Schematic Diagram of System Power Relations
1.2.2 电压约束

式中,Ui为母线i的电压;Uimin,Uimax分别为母线i电压的下限值和上限值。
1.2.3 电流约束

式中,Ii为第i条支路的电流值;Iimax为支路i的允许电流上限值。
1.2.4 容量约束

式中,Pi、Qi为第i条支路的有功功率和无功功率;Simax为改支路的允许容量上限值。
1.2.5 网络结构约束

式中,gk为重构后的配网结构;G为所有可行配网结构的集合。
1.3 计算复杂性
配电网络重构是多目标、非线性整数组合优化问题[6]。由于系统中的联络开关和分段开关数量巨大,开关状态的排列组合数目也非常庞大,如果系统中有n个操作开关,将出现2n种组合情况。使用穷举法进行配网重构优化,当网络规模较大时,有可能面临组合爆炸而不可行。另外,由于配网重构的目标函数多为网损最小化,在网络重构过程中,要不断地进行配电网络潮流计算,需要耗费大量时间,这决定了对算法的选择十分关键。
目前,国内外研究较多的配网重构方法主要有启发式方法、随机优化方法和智能化方法,具体的算法包括:支路交换法、最优潮流模式法、模拟退火算法、遗传算法、蚁群算法、粒子群算法、神经元网络法和专家系统法等。实际应用中,可以根据配电网的具体情况选择优化算法,也可使用组合算法优化配网重构问题,如文献[6-8]。下面将简单介绍常用的配电网重构算法。
2 配电网重构算法
2.1 启发式方法
2.1.1 支路交换法
支路交换法[9-10](Branch Exchange)又称开关交换法(Switch Exchange),是由S Civanlar等人提出的[11],该算法一般以有功网损最小为目标函数,利用联络开关和分段开关的开合实现负荷在支路间的转移,当闭合一个联络开关时,要打开相应环路上的一个分段开关才能使配电网络保持辐射状,相当于交换了联络开关和分段开关所在的支路。考虑如下启发式规则:当联络开关两端的电压差较明显时,闭合此开关可减少网损;负荷一般由电压低的一侧向电压高的一侧转移。
支路交换法缩小了可行解空间,进而提高了计算效率,并且可以估算出负荷在支路间转移后实现的网损减小值:
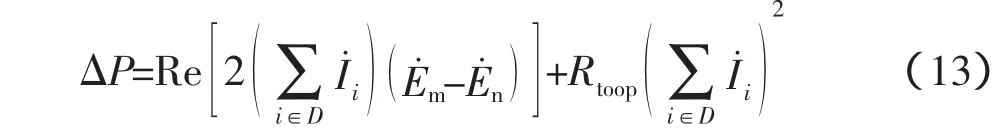
式中,△P为系统中重构后有功网损减少值;D为负荷转移区域的节点集合;I觶i为节点i负荷转移前的电流;E觶m为联络开关电压降落较小侧的电压降;E觶n为联络开关电压降落较大侧的电压降;Rtoop为联络开关闭合后环路的串联电阻。
2.1.2 最优流模式法
最优流模式法(Optimal Flow Pattern)[12-13]是由Darish Shrimohammadi等人于1989年提出的一种启发式算法。最初的最优流模式法开始时闭合系统中的所有联络开关,形成一个弱环网,利用电压将负荷转换为电流注入相应节点,并用支路的电阻代替阻抗,在满足基尔霍夫电流定律和电压定律的条件下,求得系统最优潮流模式,然后打开最优流最小支路上的开关,重复进行直至网络恢复辐射状。改进的最优流模式法对联络开关进行逐个闭合,并计算每次闭合的联络开关对应环路的最优流,打开最优流最小支路上的开关,重复以上过程,直至系统网损不再减少。递归虚拟流[14]也是一种改进的最优流模式法,该方法采用逐个闭合联络开关的模式,估算对应环网上每个开关打开后的网损减少值,选择网损减少最大的支路打开开关,重复进行直至系统网损不再减少。以上各种方法中,如果选择的最优支路不能满足系统的约束条件,则用次优支路代替。
2.2 随机优化方法
2.2.1 模拟退火算法
模拟退火算法[15](Simulated Annealing)源于对固体退火过程的模拟,可用于求解大规模的组合优化问题。退火的过程为:将固体加热至充分高的温度,再将其徐徐冷却,加热时由于固体内部粒子变为无序状而内能增大,冷却时粒子逐渐变得有序,在每个温度点都达到平衡,在常温时达到基态,此刻固体的内能最小。
模拟退火算法通常采用冷却进度表来控制,包括控制参数及其衰减因子、每个控制参数对应的迭代次数和终止准则。固体内能E模拟为系统的网损(目标函数),温度T模拟控制参数t。产生的新解被接受的概率P由Metropolis接受准则决定:

式中,△P为新解的目标函数和原解的目标函数的差值;t为控制参数。
2.2.2 遗传算法
遗传算法[6-7,16](Genetic Algorithm)是J.H.Holland教授于20世纪60年代末提出的,它源于对生物进化过程的模拟研究。遗传算法不依赖梯度寻优信息,具有自适应性和并行性,求解过程中不易陷入局部最优问题,能以较大概率求得最优解,并产生一系列次优解可供选择。遗传算法通过复制、交叉和变异产生新的后代,主要参数有群体规模、算法执行代数、复制概率、杂交概率和变异概率,这些参数的合理选取对提高算法的效率和避免局部最优解很重要。
传统的遗传算法计算过程中存在大量的不可行解,严重影响了计算速度,在进行配电网重构优化时,应结合配电网的实际情况和特点设定约束条件,以提高算法的效率。
2.2.3 蚁群算法
蚁群算法[17-18](Ant Colony Algorithm)是意大利学者Maniezzo,Colorni和Dorigo等人于20世纪90年代提出的,源于模拟自然界蚂蚁的寻径行为。蚁群在寻找路径时会释放出一种特殊的信息素,蚂蚁通过的路径越短时,释放的信息素浓度越高。在蚁群寻径过程中,信息素浓度较高的路径被选中的可能较大,其信息素浓度也会不断累加,而其他路径随着时间流逝信息素浓度逐渐降低,最终蚁群会找到最短路径。
蚁群算法应用在配电网络重构中,蚂蚁经过的路径为辐射状,优化目标常采用最小化网损,并考虑支路电压、电流和网络结构等约束条件。
2.2.4 粒子群算法
粒子群优化算法[19-20](Particle Swarm Optimization)是美国的Kennedy和Eberhart博士于1995年提出的,源于对鸟群觅食过程的模拟。粒子群算法是将群体中的每个个体视为没有质量和体积的“粒子”,这种“粒子”自身具有的速度矢量决定该“粒子”的飞行距离和方向。“粒子”在飞行过程中根据自己发现的最优位置和群体发现的最优位置对速度矢量做出调整,从而形成寻优的正反馈。粒子群对个体和群体的最佳位置进行记忆追踪,最终到达整个空间的最优位置。
粒子群算法应用于配电网重构问题,为了避免大量无用粒子的产生,可以先对配电网络划分为若干个支路组,利用轮盘赌法选取需要打开开关的支路组,再对这些支路组进行内部优化,这样可有效地提高计算速度。
2.3 智能化方法
2.3.1 人工神经网络法
人工神经网络法[21-22](Artificial Neural Network)是一种模仿动物神经网络行为的并行信息处理算法。用该算法进行优化时,神经网络稳定状态与实际问题的最优解相对应,神经网络演化过程与实际问题的优化过程相对应。
人工神经网络法有较强的非线性映射并行计算能力,且应用于配电网重构问题时不需要进行潮流计算,大大节省了计算时间,但是其优化结果对训练组数据的依赖性很强,而配电网中负荷和网络结构变化频繁,要不断改变该算法的权值,导致其实用性受到影响。
2.3.2 专家系统法
专家系统法(Expert System)是模拟实际工作中靠工作人员积累的经验对开关进行操作的方法。文献[22]提出了基于专家系统的配电网络重构方法:根据对实际配网的研究及从调度人员处了解来的经验,这种方法可以在一定程度上达到减少网损的目的。由于专家系统法处理复杂问题时耗时长,且不能保证得到最优开关组合,不适用于大规模、对供电指标要求较高的现代配电系统。
3 结语
配电网重构对提高系统运行的安全性、经济性和供电质量等具有深远的影响。对配网重构问题的研究不能局限于优化算法,还应注重负荷预测、潮流计算等和配网重构密切相关的课题研究,考虑无功优化和分布式电源的加入对配网重构的影响,开展具有实用价值的实时配网重构研究。
[1]TALESKIR,RAJICICD.DistributionNetworkReconfiguration for Energy Loss Redution[J].IEEE Trans on Power Systems,1997,12(1):398-406.
[2]王守相,王成山.现代电力系统分析[M].北京:高等教育出版社,2007.
[3]张大海,江世芳,赵建国.配电网重构研究的现状与展望[J].电力自动化设备,2002,22(2):75-76.
ZHANG Da-hai,JIANG Shi-fang,ZHAO Jian-guo.The Achievements and Prospect of Distribution Network Reconfigution Research[J].Electric Power Automation Equipment,2002,22(2):75-76.
[4]陈方亚.对配电网重构算法的分析[J].广东科技,2008(11):141-142.
CHEN Fang-ya.Analysis of Distribution Network Reconstruction Algorithm[J].Guangdong Science&Technology,2008(11):141-142.
[5]韩学军,陈鹏,国新凤,等.基于潮流计算的配电网重构方法[J].电网技术,2007,31(17):60-63.
HAN Xue-jun,CHEN Peng,GUO Xin-feng,et al.A Power Flow Based Reconfiguration Method of Distribution Network[J].Power System Technology,2007,31(17):60-63.
[6]张雨佳.遗传退火算法在城市配电网重构中的应用[D].天津:天津大学电气与自动化工程学院,2007.
[7]王林川,梁栋,于冬皓,等.基于遗传和禁忌搜索混合算法的配电网重构[J].电力系统保护与控制,2009,37(6):27-30.
WANG Lin-chuan,LIANG Dong,YU Dong-hao,et al.Distribution Network Reconfiguration Based on Genetic/Tabu Search Hybrid Algorithm[J].Power System Protection and Control,2009,37(6):27-30.
[8]陈曦,程浩忠,戴岭,等.邻域退火粒子群算法在配电网重构中的应用[J].高电压技术,2008,34(1):148-153.
CHEN Xi,CHENG Hao-zhong,DAI Ling,et al.Application of Simulated AnnealingParticleSwarm Optimization Algorithm in Reconfiguration of Distribution Networks[J].High Voltage Engineering,2008,34(1):148-153.
[9]戴光武,都洪基,贾磊,等.基于支路交换法的配电网重构研究[C]//2008中国电力系统保护与控制学术研讨会论文集:345-348.
DAI Guang-wu,DU Hong-ji,JIA Lei,et al.Research on Distribution Network Reconfiguration Based on the Branch Exchange Algorithm[C]//2008China Electric Power System Protection and Control Proceedings:345-348.
[10]LABOURDETTE J-F P,HART G W,ANTHONY A S.Branch-Exchange Sequences forReconfiguration of Lightwave Networks[J].IEEE Transactions on Communications,1994,42(10):2822-2832.
[11]CIVANLAR S,GRANGER J J,YIN H.Distribution Feeder Reconfiguration for Loss Reduction[J].IEEE Trans on Power Delivery,1983,3(3):1217-1223.
[12]刘蔚,韩祯祥.基于最优流法和遗传算法的配电网重构[J].电网技术,2004,28(19):29-33.
LIU Wei,HAN Zhen-xiang.Distribution Network Reconfiguration Based on Optimal Flow Pattern Algorithm and Genetic Algorithm[J].Power System Technology,2004,28(19):29-33.
[13]雷健生,邓佑满,张伯明.综合潮流模式及其在配电系统网络重构中的应用[J].中国电机工程学报,2001,21(1):57-62.
LEI Jian-sheng,DENG You-man,ZHANG Bo-ming.Hybrid Flow Pattern and Its Application in Network Reconfiguration[J].Proceedings of the CSEE,2001,21(1):57-62.
[14]邓佑满,张伯明,相年德.配电网络重构的递归虚拟流理论和算法[J].清华大学学报:自然科学版,1997,14(4):113-116.
DENG You-man,ZHANG Bo-ming,XIANG Nian-de.Recursive Fictitious Flow Theoryand Algorithm for Distribution Network Reconfiguration[J].Journal of Tsinghua Univesity:Sci&Tech,1997,14(4):113-116.
[15]张步涵,沙立华,曾次玲.基于随机生成树的配电网重构模拟退火算法[J].华中科技大学学报:自然科学版,2005,33(6):76-79.
ZHANG Bu-han,SHA Li-hua,ZENG Ci-ling.Simulated Annealing Algorithm Based on Random Spanning Tree in Distribution Network Reconfiguration[J].J.Huazhong Univ of Sci&Tech:Nature Science Edition,2005,33(6):76-79.
[16]邓永生.遗传算法在配电网重构中的应用研究[D].重庆:重庆大学电气工程学院,2002.
[17]张云,海涵.基于蚁群算法的配电网重构[J].科技信息,2008(33):351-352.
ZHANG Yun,HAI Han.The Reconstruction of Distribution NetworkBasedonAntColonyAlgorithm[J].Science&Technology Information,2008(33):351-352.
[18]DORIGO M,MANIEZZO V,COLORNI A.Ant System:OptimizationbyaColonyofCooperatingAgents[J].IEEETrans onSystems,ManandCybernetics-PartB:Cybernetics,1996,26(1):29-40.
[19]KENNEDYJ,EBERHARTR.ParticleSwarmOptimization[C]//Proceedings of IEEE International Conference on Networks.Perth,Australia,1995:1942-1948.
[20]徐立雄.基于粒子群优化算法的配电网络重构[D].成都:四川大学电气信息学院,2006.
[21]SALAZAR H,GALLEGO R,ROMERO R.Artificial Neural Networks and Clustering Techniques Applied in the Reconfiguration of Distribution Systems[J].IEEE Transactions on Power Delivery,2006,21(3):1735-1742.
[22]SARFI R J,SALAMA M M A,CHIKHANI A Y.A Survey of the State of the Art in Distribution System Reconfiguration for System Loss Reduction[J].Electric Power System Research,1994(31):61-67.
Overview on Algorithms of Distribution Network Reconfiguration
LI Fei1,QIU Zheng-mei2,MA Li3,ZHU Tie-ming4
(1.Linfen Power Supply Bureau,Linfen 041000,Shanxi Province,China;2.Weifang Power Supply Bureau,Weifang 261000,Shandong Province,China;3.China Electric Power Research Institute,Beijing 100192,China;4.Xiaoshan Power Supply Bureau,Hangzhou 311201,Zhejiang Province,China)
Reconfiguration of the distribution network can improve operation safety,economical efficiency and power supply quality,and it is of great significance to the construction and application of the distribution automation system ongoing in China.This paper introduces the optimization objective and constraints of the distribution network reconfiguration,and analyzes the complexity and difficulties in calculation,and overviews a variety of algorithms,including the heuristic,stochastic optimization and intelligent methods.In the end,the paperpoints outthe research direction which deserves sufficient attention.
distribution network;reconfiguration;optimization objectives
配电网重构可以提高配电网运行的安全性、经济性和供电质量,对于当前国内配电自动化系统建设和应用具有重要意义。介绍了配电网重构的优化目标和约束条件,分析了计算的复杂性,对配电网重构的各种算法作了综述,包括启发式方法、随机优化方法、智能化方法,指出了值得关注的研究方向。
配电网;重构;优化目标
1674-3814(2011)12-0076-07
TM 711
A
2010-05-31。
李 飞(1986—),男,助理工程师,主要研究方向为电力系统继电保护;
邱正美(1986—),女,助理工程师,主要研究方向为城市电网规划;
马 丽(1986—),女,助理工程师,主要研究方向为城市电网规划;
朱铁铭(1973—),男,工程师,主要研究方向为城市电网规划。
(编辑 冯露)
