潜热型纳米流体粘度特性的实验研究
2011-06-20
(重庆大学低品位能源利用技术及系统教育部重点实验室 重庆 400044)
纳米流体作为一种新型的功能流体,其较高的导热系数在强化传热领域具有极大的吸引力。潜热型纳米流体TiO2-BaCl2-H2O是将纳米粒子均匀分散于BaCl2水溶液中形成的悬浮液。纳米粒子TiO2既起着成核剂的作用,又可显著提高蓄冷材料的导热系数,达到强化换热的目的[1-5]。但纳米粒子的存在,在显著改善蓄冷材料热物性的同时,也改变了其另外一个热物性参数—粘度。粘度对潜热型纳米流体的悬浮稳定性以及流动阻力有很大影响。已有文献[6-9]对悬浮有毫米或微米级固体粒子悬浮液的粘度进行了研究,并建立了悬浮液粘度的理论模型。但由于纳米粒子的溶剂化效应,传统的理论模型可能不适用于潜热型纳米流体。
这里对潜热型纳米流体TiO2-BaCl2-H2O的粘度进行了实验测量,分析粘度随温度和纳米粒子体积分数的变化关系,并根据剪切应力与剪切速率之间的关系判断其是否为牛顿型流体。并基于实验数据检验现有粘度公式对潜热型纳米流体的适用性,提出新的粘度计算模型。
1 潜热型纳米流体的制备及粘度测量
采用直接共混法,将TiO2纳米粒子与BaCl2水溶液直接混合,再加入复合分散剂,然后经超声震荡5小时,即可制备出均匀稳定的潜热型纳米流体TiO2-BaCl2-H2O。分散剂的浓度为0.5%,pH值为10。图1为纳米TiO2体积分数为1.13vol%时,潜热型纳米流体TiO2-BaCl2-H2O的TEM图像,纳米粒子没有发生严重的团聚现象。
粘度测量仪器为NXE-1B型锥板粘度计,样品温度通过循环恒温浴槽精确控制。
测量工况:样品温度分别为-8、-5、0、5、10、15、20℃;样品中纳米TiO2体积分数分别为0、0.167%、0.283%、0.565%、1.13%。图2给出了各种浓度下潜热型纳米流体TiO2-BaCl2-H2O的照片。
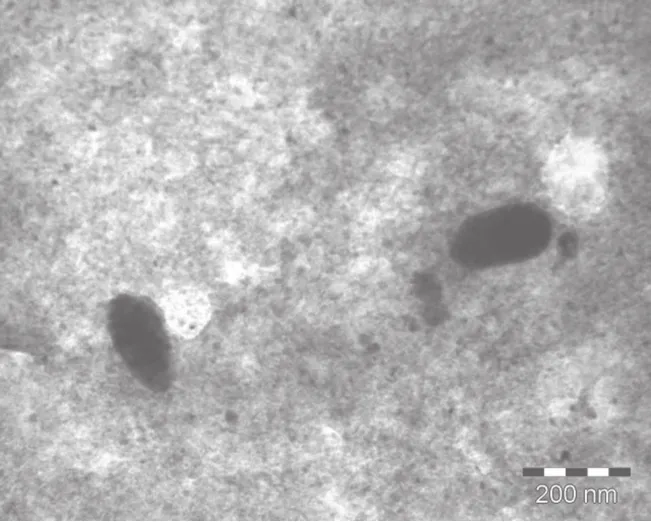
图1 潜热型纳米流体的TEM 图像(w(TiO2)=1.13%,pH=10)Fig.1 TEM of latent heat nano fl uids TiO2-BaCl2-H2O(w(TiO2)=1.13%, pH=10)

图2 潜热型纳米流体TiO2-BaCl2-H2O 照片Fig.2 Photos of TiO2-BaCl2-H2O in different volume fraction
2 实验结果与分析
图3为潜热型纳米流体TiO2-BaCl2-H2O的粘度随温度的变化曲线。同常规流体一样,潜热型纳米流体的粘度随温度的变化也非常敏感。随着温度的升高,粘度不断降低,在-8℃到10℃之间曲线变化较陡,随后曲线趋于平缓。图3也给出了粘度随纳米粒子体积分数的变化情况。0%表示BaCl2水溶液中没有添加纳米粒子。从图3中可以看出,纳米粒子浓度是影响粘度的重要因素。各种浓度的潜热型纳米流体粘度均大于BaCl2水溶液的粘度,并且浓度越高,粘度呈加速上升的趋势。比如在0℃时,w(TiO2)=0.167%的粘度比BaCl2水溶液粘度增加了2.86%,w(TiO2)=0.283%时增加了6.19%,w(TiO2)=0.565%时增加了15.24%,在浓度为w(TiO2)=1.13%时猛增了31.9%。这是因为当浓度提高到一定程度后,纳米粒子之间以及纳米粒子与溶液分子之间的内摩擦力迅速增大,宏观表现为粘度的增加。
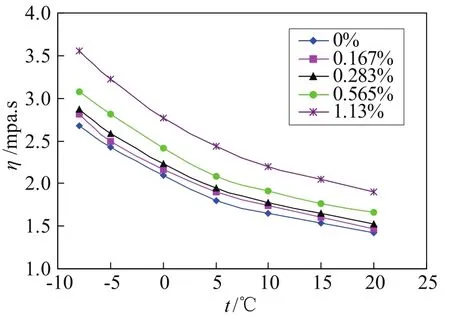
图3 TiO2-BaCl2-H2O 粘度随温度的变化曲线Fig.3 Viscosity vs. temperature curve of TiO2-BaCl2-H2O
根据剪切应力与剪切速率的关系是否遵守牛顿定律,可以判断潜热型纳米流体是牛顿型流体还是非牛顿型流体。前者的粘度不随剪切速率的变化而变化,其剪切应力τ与剪切速率D呈正比,即τ=ηD。对于牛顿型流体,单用粘度η就足以表示其流变特性。而对于非牛顿型流体,剪切应力与剪切速率间无正比关系,比值τ/D不是常数,而是剪切速率的函数。
根据胶体的流变学理论,浓度越高的胶体其流变行为越偏离牛顿型流体。若1.13vol%的潜热型纳米流体为牛顿型流体,则浓度更低的一定也为牛顿型流体。因此,仅对浓度最高的潜热型纳米流体TiO2-BaCl2-H2O进行了流变特性测量(见图4)。在两种温度下(0℃和5℃),τ-D的关系均为直线,且均通过坐标原点,所以被测流体为牛顿型流体。此外,从τ-D直线关系可见,直线的斜率越大,潜热型纳米流体TiO2-BaCl2-H2O的粘度就越大。
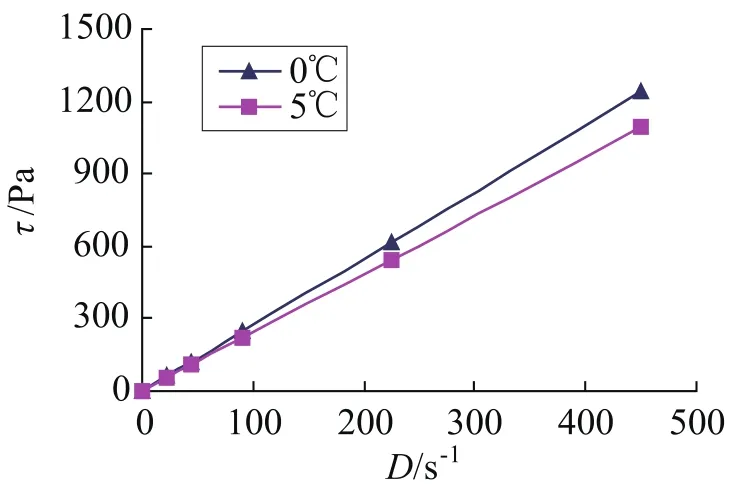
图4 TiO2-BaCl2-H2O 的流变曲线Fig.4 Rheology curve of TiO2-BaCl2-H2O
3 粘度计算模型的建立
3.1 现有粘度经验公式的适用性分析
目前许多计算粗颗粒悬浮液粘度的半经验公式大多数是由Einstein粘度公式演变而来。对低浓度的胶体溶液或悬浮液,Einstein[8]推导出式(1)所示的关系式。对较高浓度的悬浮液,Brinkman[9]建议将Einstein粘度公式改为式(2)的形式。刘玉东等[10,11]基于纳米流体TiO2-H2O粘度实验数据,将Brinkman公式进行改进,建立了适用于纳米流体TiO2-H2O粘度的计算式(3)。式中Φ为体积分数,η0为基液的粘度。
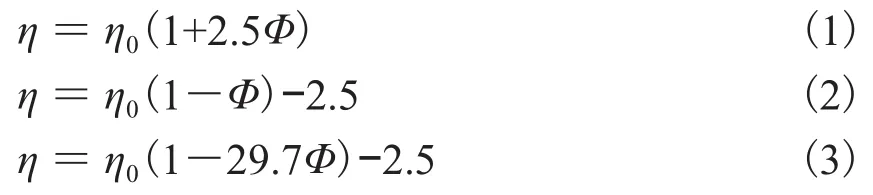
将式(1)~(3)的计算值与测量值进行比较,结果如图5所示。可见,现有经验公式Einstein公式、Brinkman公式的计算值(二者几乎重合)均比实测值偏小;而适用于纳米流体TiO2-H2O的式(3)计算值比实测值偏大,而且浓度越高这种偏离越严重。这表明,现有经验公式不能适用于潜热型纳米流体TiO2-BaCl2-H2O,需要建立新的计算模型。
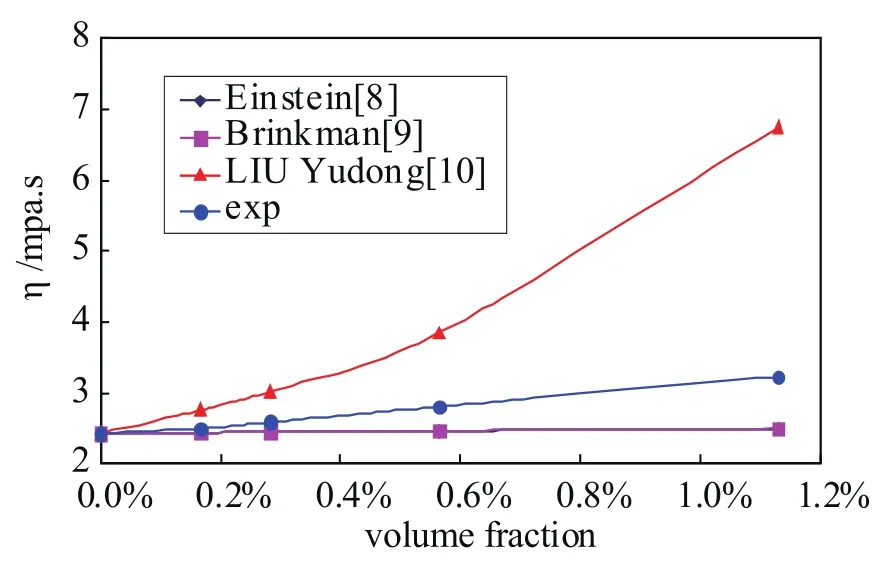
图5 已有模型预测值与实验值的比较(Einstein 和Brinkman 的计算值重合)Fig.5 Comparison between the prediction values and the experimental data
3.2 潜热型纳米流体粘度模型的建立
影响粘度大小的一个重要因素是纳米粒子表面的溶剂化效应。溶剂化效应是指溶剂分子将纳米粒子表面包裹起来,形成一定厚度的规则液体层,使纳米粒子的有效尺寸增大的现象[12,13]。溶剂化效应导致纳米粒子的有效体积分数增大。显然,传统粘度模型中均未考虑溶剂化效应,导致计算值严重偏离测量值。根据Paul C.Hiemenz的推导[14],纳米粒子的有效体积分数Φeff可表示为:

式中ΔR为溶剂化层的厚度,R为纳米粒子半径(30nm)。通过实验研究得知,ΔR≈35.54 nm。表明水分子及分散剂分子在纳米粒子表面包裹了厚度约为35.54nm的溶剂化层,使纳米粒子的有效尺寸大大增加,见图6所示。
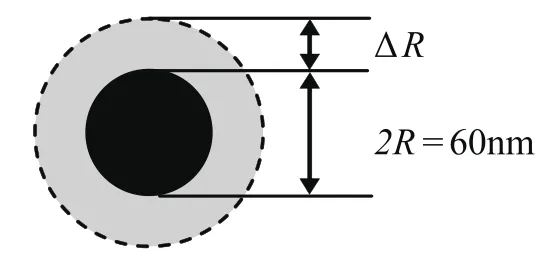
图6 溶剂化层模型Fig.6 Solvable layer Model
将式(3)中的Φ用式(4)的Φeff代替,可以得出新的计算模型见式(5)。新计算模型的预测值与实验值的对比如图7所示,预测值与实验值极其吻合,相对误差小于2%。
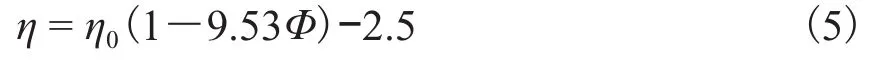
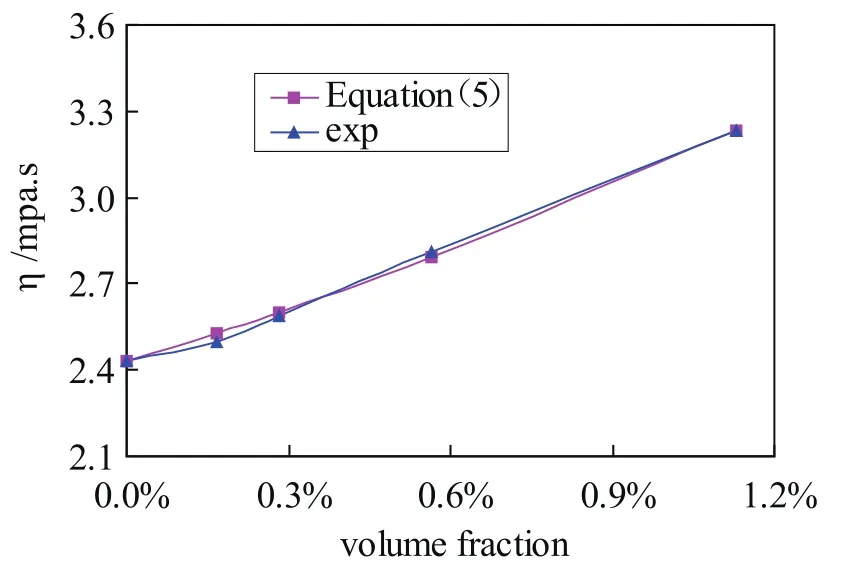
图7 新粘度模型预测值与测量值的对比Fig.7 Comparison between the prediction values of the new model and the experimental data
4 结论
1)在BaCl2水溶液中添加纳米TiO2会增加其粘度,随着粒子浓度的增加,粘度增加越显著。
2)潜热型纳米流体TiO2-BaCl2-H2O表现为牛顿型流体的流变特性,其粘度不随剪切应力的变化而变化。
3)现有的粘度经验公式由于未考虑纳米粒子表面的溶剂化效应,不适用于潜热型纳米流体TiO2-BaCl2-H2O。
[1] Xuan Y, Li Q. Heat Transfer Enhancement of Nanof l uids[J]. International Journal of Heat and Fluid Flow, 2000,21(1): 58-64.
[2] Liu Yudong, Zhou Yueguo, Tong Mingwei. Experimental Study of Thermal Conductivity And Phase Change Performance of Nanofluids PCMs[J]. Microfluidics and Nanof l uidics, (2009)7: 579-584.
[3] Liu Yudong, Li Kuining, He Qinbo. Study on ThermalProperties of Low Temperature Nanocomposites for Phase Change Cool Storage[J]. Journal of Engineering Thermophysics,2008 29(1):105-107.
[4] Peng Xiaofei, Yu Xiaol, Xia Lifeng, et al. Prediction of effective thermal conductivity of nanof l uids[J]. Journal of Chemical Industry And Engineering(China), 2007 58(2):299-303.
[5] Lin Jing, Fang Liguo. Recent progress of technology and application of heat transfer enhancement of nanofuilds[J].Chemical Industry And Engineering Progress, 2008 27(4): 488-494.
[6] Li Decai.Theory and Application of Magnetic Fluid[M].Beijing: Science Press, 2003.
[7] Thoms D G. Spherical Particles, in Transport Characteristics of SusPension: Vlll. A Note on the Viscosity of Newionian Suspensions of Uniform[J]. J.Colloid Sci., 1965, 20: 267-277.
[8] Einstein, A.Investigations on the Theroy of the Browmain Movement[M]. Dover, New York, 1956.
[9] Brinkman, H C. The Viscosity of Concentrated SusPensions and Solutions[J]. J. Chem. Phys., 1952, 20:571-581.
[10] Liu Yudong, Li Kuining, Tong Mingwei. Viscositycorrection Equations of TiO2-water nanof l uids[J]. Journal of Chongqing University,2006, 29(9): 52-55.
[11] He Qinbo, Tong Mingwei, Liu Yudong. Experimental study on viscosities of TiO2-H2O nanofluids. Chemical Industry and Engineering Progress, 2009, 28(1): 37-40.
[12] Zhang Kejia, Peng Xiaofeng,Wang Buxuan. Particlebubble collision in nanof l uids. Journal of Thermal Science And Technology, 2009 8(1) : 35-38.
[13] Lu Qian, Xiang Liqin, Huang Jingxing, Zhao Xiaopeng.Synthesis and Rheological properties of TiO2-oil Nanofluids. Chinese Journal of Materials Research,2008 22(5): 500-504.
[14] Paul C Hiemenz, Raj Rajagopalan. Principles of Colloid and Surface Chemistry. Marcel Dekker, 1997.
