空间目标成像原理及运动控制
2011-06-19陈乾辉王小芬
陈乾辉,王小芬
(1.商丘科技职业学院 机电工程系,河南 商丘 476000;2.商丘科技职业学院 计算机科学系,河南 商丘 476000)
0 引 言
近年来,随着计算机视觉技术的飞速发展,在目标追踪、定位、识别及智能控制方面有了广泛应用。它从摄像机获取的图像信息出发,计算三维空间中物体的几何信息,而空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系是由摄像机成像的几何模型决定,因而完成映射到单幅或多幅图像上的三维场景,如三维场景的重建。
运动目标的序列图像跟踪要用一种算法来实现,然而由于其轨迹的不确定性,因此可以通过摄像机的运动控制来实现,即可以通过摄像机的左右平移和俯仰旋转,获取物体的三维姿态信息进行三维建模,得到目标的模拟轨迹。
1 摄像机标定
为获得摄像机的内部参数,在大多数条件下这些参数必须通过实验与计算才能得到,这个过程被称为是摄像机定标。摄像机的内部参数指摄像机成像的基本参数,如主点,摄像机的外部参数指摄像机相对于外部世界坐标系的方位,而摄像机标定目的就是获取某些内外参数。计算机视觉中几何模型参数就是摄像机参数。
现有的摄像机定标技术大体可以归结为两类:传统的摄像机定标方法和摄像机自定标方法。
传统摄像机定标方法有4类:
1)利用最优化算法的定标方法;
2)利用摄像机变换矩阵的定标方法;
3)进一步考虑畸变补偿的两步法;
4)采用更为合理的摄像机成像模型的双平面定标方法。
摄像机自定标方法有4类:
1)利用本质矩阵和基本矩阵的摄像机定标方法;
2)利用绝对二次曲线和外极线变换性质的摄像机定标方法;
3)利用主动系统控制摄像机做特定运动的自定标方法;
4)利用多幅图像之间的直线对应关系的摄像机定标方法。
总之,摄像机标定在从计算机图像坐标中导出三维几何信息以及由三维信息导出二维计算机图像坐标的应用中起着重要作用。
2 摄像机成像原理
摄像机成像模型包括常用投影和针孔成像模型。常用投影又分为中心投影和平行投影,即投影射线汇聚于一点的投影称为中心投影,投影射线相互平行的投影称为平行投影。而对于三维空间物体到像平面的投影关系称为成像模型,其中理想投影成像模型则称针孔模型。
2.1 成像模型
在空间目标成像模型中,为确切掌握空间目标的姿态信息,必须将其坐标转换到同一坐标系下。因此定义了3个坐标系:O-XYZ 坐标系是世界坐标系,乃用户定义坐标系,表示场景点的绝对坐标。OC-XCYCZC是摄像机坐标系,其中,OC为摄像机光心,ZC轴与摄像机的光轴重合,取摄影方向为正向。O′xy是图像坐标系,表示场景点在图像平面上的投影。XC轴、YC轴分别与X 轴、Y轴平行,ZC是摄像机的光轴,它与图像平面垂直。三坐标系之间的转换关系见表1。

表1 坐标转换
物点、光心和像点三点共线,且fx,fy,u0,v0为摄像机内部参数,r11,r22,…,r33是正交旋转矩阵的系数。
取f为摄像机焦距,光轴与图像平面交点,O′为图像坐标系的原点,选取飞行器的某点P(X,Y,Z)作为目标点,在图像平面上的投影点为p(x,y),成像几何模型如图1所示。

图1 成像几何模型
在不考虑摄像机镜头畸变的情况下,可得透视投影成像模型(其中:(x,y)为像点坐标,(XS,YS,ZS)为摄影中心坐标,a1,a2,a3,b1,b2,b3,c1,c2,c3为坐标变换中矩阵元素,且当变换关系一定时,变换矩阵元素已知)为:
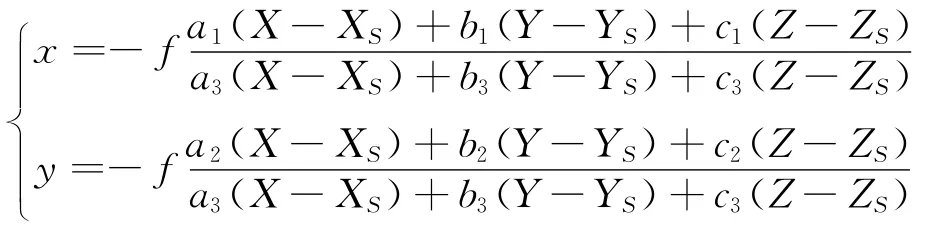
2.2 极线约束
根据外极线几何理论,三维空间一点在两个像平面上的投影点称为对应点对,且对应点对中的一点位于另一个点所确定的外极线上,如图2所示。
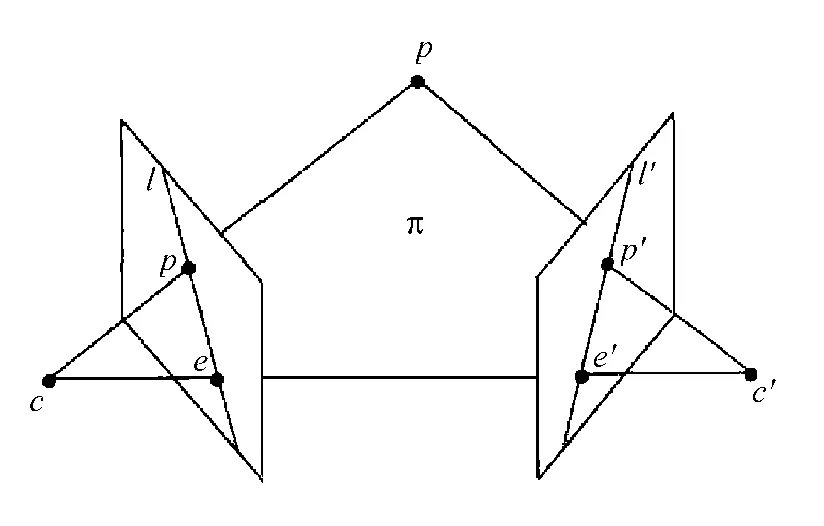
图2 极线几何约束关系

假定以经纬仪C为测量坐标系的基坐标系,得关系式

3 摄像机运动控制及算法实现
为获得序列图像以掌握空间目标运动,必须了解图像的运动轨迹。摄像机一般固定在光电设备上,由于光电设备围绕地球坐标轴左右摆动和上下俯仰,其坐标变换相当复杂,不适宜平移运动,若旋转是围绕以图像平面为中心的系统,则推导就相对简单。因此,根据所作用的信号,这里采用光电设备的左右平移运动或使用摄像机的上下俯仰运动,以获取图像信息。
3.1 图像平面位置变化的影像
跟踪系统的结构和数字模型如图3所示。
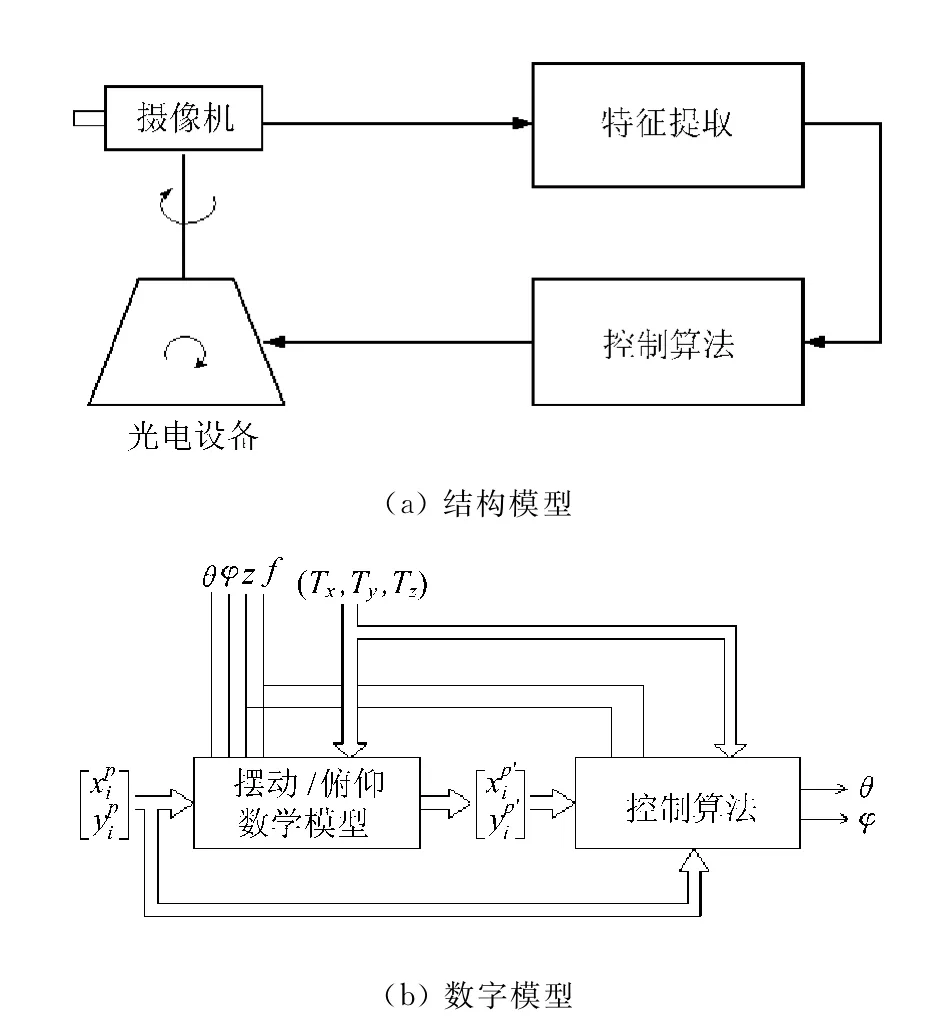
图3 跟踪系统模型
该系统由光电设备上的摄像机、图像处理系统和控制光电设备的计算机接口3大部分组成。所需要建立的模型是描述原始图像坐标()和经过摆动和俯仰运动的图像点坐标之间的关系。
坐标变换依赖于摄像机焦距f,左右摆动角φ、俯仰角θ和地球坐标系原点与图像平面坐标原点偏移量(Tx,Ty,Tz)、原始物体点(x,y,z)与图像点(xi,yi)之间的差,以及经过左右和俯仰运动的物体点(x′,y′,z′)与图像点()之间的差值,坐标变换见表2。

表2 摆动和旋转坐标变换

表3 图像平面(物理)之间坐标关系
3.2 摄像机运动的控制算法
为得到偏差矢量T=(Tx,Ty,Tz)的精确值,我们对变换公式进行了研究,发现当伸缩比很大时,可以忽略该偏差影响。并由可以用逼近,忽略上述方程中的。当很大时,得图像平面(物理)之间坐标关系及三维姿态角(见表3)。
4 结 语
通过摄像机成像原理以及空间目标三维转换模型的分析,使我们了解坐标变换的重要作用,并由摄像机运动控制及算法的实现算出了空间目标三维姿态角,此研究对目标特性视觉化具有重要的理论和现实意义。
[1]王巧华,文友先,刘俭英.我国机器视觉技术的发展前沿[J].农机化研究,2000,11(4):16-18.
[2]张祖勋,张剑清.数字摄影测量学[M].武汉:武汉大学出版社,1997:1-6.
[3]Armin Gruen.Digital photogrammetric stations re-visited[J].Int.Arch.Of Photo-grammetry and Remote Sensing,1996,31(B/2):127-134.
[4]张祖勋.数字摄影测量的发展与展望[J].地理信息世界,2004,2(3):1-5.
[5]张祖勋,张剑清.数字摄影测量在我国的发展与应用[EB/OL].(2010-04-25)[2011-08-20].http://wenku.baidu.com/view/18a75f649b6648d7c1c74672.html.
[6]张祖勋.数字摄影测量与计算机视觉[J].武汉大学学报:信息科学版,2004,29(12):1035-1039.
[7]袁野.摄像机标定方法及边缘检测和轮廓跟踪算法研究[D]:[博士学位论文].大连:大连理工大学,2002.
[8]王之卓.摄影测量原理[M].武汉:武汉大学出版社,2007.
