基于小波变换的输电线单相接地故障测距算法

贾文超，苏丽娜，陈 刚

（长春工业大学 电气与电子工程学院，吉林 长春 130012）

0 引 言

随着我国电力系统的不断发展，高压、长距离输电线路越来越多，由于输电线路的距离一般都较长，经过的地形也十分复杂，加之天气等自然因素的影响，发生故障是不可避免的。输电线路可能发生的故障中，单相接地故障是发生最多且危害最大的，因此，文中着重对此进行研究。输电线路发生故障之后，不仅会影响到电力系统安全稳定的运行，还会危及到人们的日常生活，故障排除所需的时间越长，造成的损失越大，对电力系统的冲击也越大。所以，线路故障点的准确快速定位日益重要。如果能够及时发现故障并且确切地进行故障的定位，可以有效地缩短故障的时间，及时发现电力系统隐患，节省人力物力，减小对电力系统和人们日常生活的影响，具有巨大的社会效益和经济意义。

由于行波测距与传统的阻抗法和故障分析法测距相比具有测距准确、可靠且经济方便等优点，日益成为关注的焦点和热点［1］。近几年行波测距法的研究主要集中在A型单端测距和D型双端测距方法上。行波测距法是利用故障时线路中产生的暂态行波在故障点和母线之间来回一趟所需要的时间，或故障行波到两端母线的时间差与故障行波波速的乘积来计算故障点的位置［2］。

文中利用有数学显微镜之称的小波变换法来确定故障行波波头到达的时间，小波变换解决了傅里叶分析的基本矛盾，即频域和时域局部化的矛盾，它能对于信号细节进行分析，进而实现对于信号奇异点的检测，完成故障点的精确定位。

1 行波故障测距原理

输电线路发生故障的时候，将在故障点处产生向线路两端相反方向传播的行波。行波会在系统中来回折射和反射直到进入稳态。

根据分步参数模型，把输电线路看成均匀无损线路，大地和导线的电阻忽略不计，则输电线路波速度为［3］：

1.1 单端行波测距法

当线路发生故障时，故障点将产生向线路两端母线传播的电流和电压行波，故障行波在传播的过程中在故障点和母线之间发生反射。故在线路母线端装设测量装置，用以检测波头和反射波头的时间差，再结合行波的波速度计算出输电线路故障点的位置。但是，由于单端测距法需要检测反射波，所以大大降低了测距的精度。

1.2 双端行波测距方法

双端测距法是以故障行波到达母线两端的时间差为时间量，时间差与行波的波速度的乘积即为输电线路故障距离。双端测距法需要在线路两端分别装设检测互感器，并且进行同步通信，以获取故障行波波头到达的准确时间。设故障初始行波波头到达两侧母线的时间分别为TS和如图1所示。

图1 双端测距原理示意图

装于线路两端的装置采集到故障行波波头到达两侧母线的时间，则：

双端测距法相对于单端测距法来说，不需要检测反射波到达母线的时间，只需通过时间同步装置GPS来确定初始行波波头到达的时间，因此双端法简单易行，便于达到较高的检测精度。

2 小波变换的原理和算法

以上两种行波测距算法，测距精度依赖于行波信号的精确采集，文中利用小波变换完成行波信号的检测。

函数f（t）的连续小波变换（简称为小波变换）可表示为：

在实际应用中，一般都需要对于连续小波尺度和平移因子进行离散化，由Mallat快速算法实现。Mallat算法就是采用小波滤波器对离散信号进行反复的低通和高通滤波过程。因此，对一离散信号的离散小波变换，其结果应包含各个尺度上的高频分量和最大尺度上的低频分量。

设低频分量为ai，高频分量为di，正交小波滤波器分别为h（低通）和g（高通），则某一尺度上的小波Mallat算法可表示为

Mallat算法如图2所示。

图2 Mallat算法

显然，信号经过小波变换后，可得到一系列不同分辨率的信号。

3 行波奇异性检测

若函数f（x）在某处间断或者某阶导数不连续，则称该函数具有奇异性。在电力系统发生故障后的暂态信号中，突变点往往标志着故障发生的时间。在故障开始后的瞬间所出现的暂态行波随着入射波和反射波等陆续到达检测点（母线），行波信号呈现尤为明显的奇异性［5］。

定义1 在某一尺度a0下，如果存在一点（a0，b0），使得

则称点（a0，b0）是局部极值点，且在b＝b0上有一过零点，如果对b0的某一领域内的任意点b，有

则称（a0，b0）为小波变换的模极大值点。

应用小波变换检测奇异点，利用卷积二进制小波变换原理，如下：

满足小波的积分值为零的条件，可证。

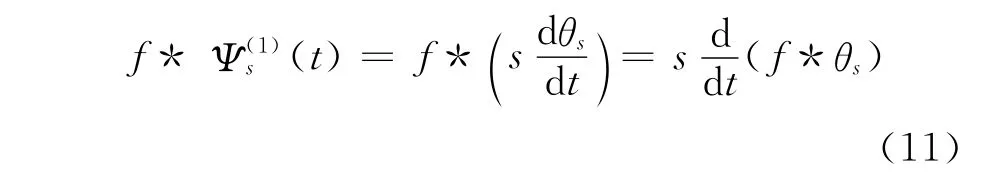
假设某未知输入函数f有一个阶跃点。通过对f的采样，可以利用差分运算来估计这个阶跃点的位置，但是由于干扰等原因，运算结果可能波动很大，应当利用卷积f＊θ事先磨光函数f以减少可能的干扰。因此，小波变换就是信号f（t）在尺度下被平滑后的一阶导数。函数的一阶导数的模为极值时，所对应的点即为函数的拐点；函数一阶导数的模为极大值时，所对应的点即为函数的突变点［6］。当小波取为光滑函数的一阶导数时，小波变换f＊模极大值点就对应于信号f（t）的突变点。

4 仿真分析

应用双端行波测距法对输电线路单相接地故障进行仿真。由于故障时产生向母线两端传播的电压和电流行波，电流行波可以通过线路两端装设的电流互感器获取，所以选择暂态电流行波作为研究对象［7］，用MATLAB进行仿真，其模型如图3所示。

由图中可见，220kV的高压输电线路，输电线路总长度为200km，故障点距母线M的距离为100km，文中以A相接地故障为研究对象。线路采用分布参数模型，线路参数为：

利用三相线路故障模块模拟A相接地故障，在母线M，N两端进行行波电流的采样，采样频率为1MHz，仿真时间为0.08s，故障发生的时间为0.03s。

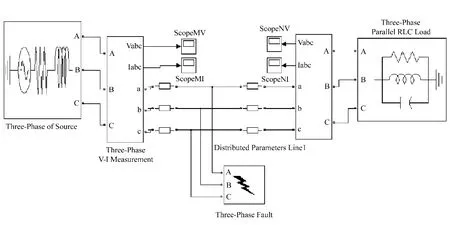
图3 MATLAB仿真模型

通过仿真和计算，得到两端母线的零序电流波形如图4所示。

图4 母线两端零序电流波形

经过小波变换，对暂态行波信号的奇异性进行检测［8］，得到母线两端行波信号的模极大值，如图5所示。

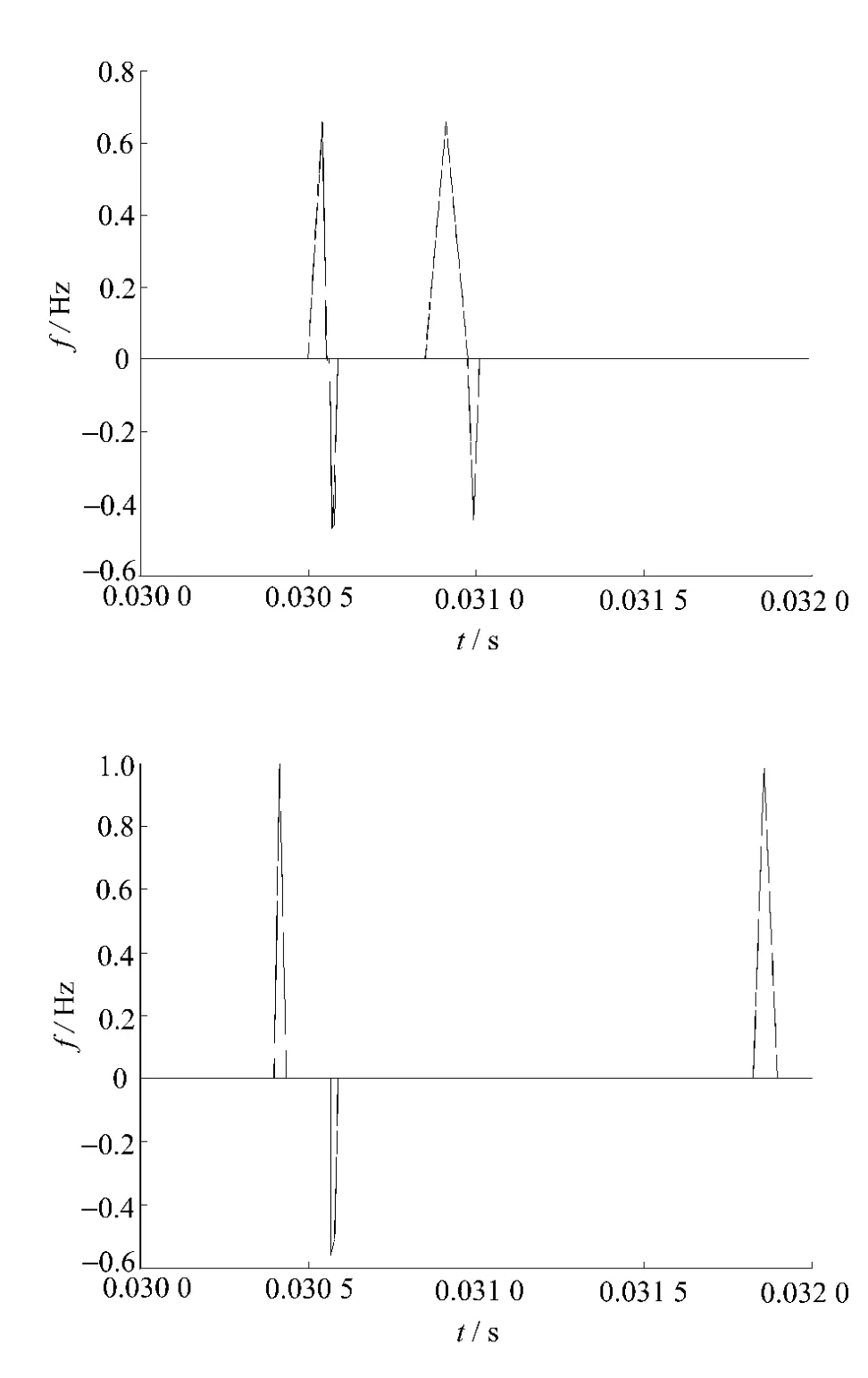
图5 小波变换提取模极大值

对模极大值进行局部放大得到母线M端和母线N端初始波头到达的时间，经计算故障点的位置为XS＝100.213km。

仿真的绝对误差为0.213km，相对误差为0.244%。

5 结 语

快速准确的输电线路故障测距具有重大的社会意义和经济意义。文中采用双端行波测距法对输电线路单相接地故障进行测距，并且利用小波变换法提取故障暂态信号的奇异点。经仿真实验证明，该方法是可行的且精度较高。仿真实验是基于实验环境，相对于实际线路来说稍显简单。要把此理论应用于实践，就要考虑到更多实际存在的复杂因素。通过仿真可知，该方法还存在一定的误差，如何缩小误差，提高精度成为未来研究的方向。

［1］马永明，陈平，刘万超，等.基于MATLAB的输电线路故障行波仿真平台［J］.山东理工大学学报，2010，5（3）：78－85.

［2］季涛，孙同景，薛永端，等.配电网故障定位技术现状与展望［J］.继电器，2005，24（33）：32－37.

［3］黄雄，王志华，尹项根，等.高压输电线路行波测距的行波波速确定方法［J］.电网技术，2004，28（9）：35－37.

［4］房雪雷，朱宁.输电线路线路故障定位技术的分析与比较［J］.安徽电气工程职业技术学院学报，2008，1（3）：30－33.

［5］李加波，于瑞红，戴玉松，等.基于小波变换的输电线路行波测距研究［J］.湖南电力，2005，25（1）：15－18.

［6］胡铭，陈珩.基于小波变换模极大值的电能质量扰动检测与定位［J］.电网技术，2001，25（3）：12－16.

［7］肖白，穆钢，黎平，等.配电网单相接地故障选线方案［J］.继电器，2005，24（33）：1－5.

［8］周明月，姜文龙.基于小波变换的图像混合去噪算法［J］.长春工业大学学报：自然科学版，2008，29（2）：162－164.