基于正交多项式的数据拟合方法

常锦才，赵龙，杨倩丽

(河北联合大学理学院，河北唐山 063009)

1 问题的提出

拟合作为函数逼近的一种方法，有着极其广泛的应用。然而在科学研究和工程实践中经常遇到如下问题，经过试验或观测得到物理量x与y的一组离散数据对(xi，yi)(i=1，2，…，m)，其中xi互异，我们希望用简单的函数y=f(x)反映物理量y与x之间的依赖关系，即函数逼近问题。本文主要讨论正交多项式对一元函数的拟合问题。一般多项式拟合时，法方程组往往是病态的，计算不稳定，选用正交多项式作为拟合工具可以得到与一般多项式拟合相同的结果，而且有效的避免病态问题。文献［4］给出了用最小二乘法求形如y=ax2+c的经验公式的方法，本文选取缺项的正交基函数也得出相同的结果。对原始数据缺失的拟合问题，本文采用曲线拼接的思想和方法，得到满足一定光滑度的分段拟合曲线，数据预测结果表明方法是可行的。

2 正交多项式

定义2.1 设φn(x)是［a，b］上首项系数an≠0的n次多项式，ρ(x)为［a，b］上的权函数，如果多项式序列{φn(x)满足

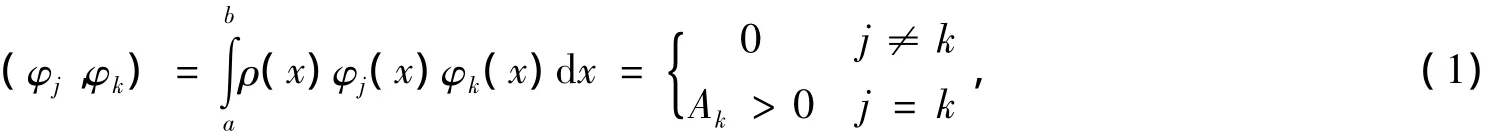
则称多项式序列{φn(x为在［a，b］上带权ρ(x)正交，称φn(x)为［a，b］上的带权ρ(x)的n次正交多项式。

定义2.2 如果函数族 φ0(x)，φ1(x)，…，φn(x)满足

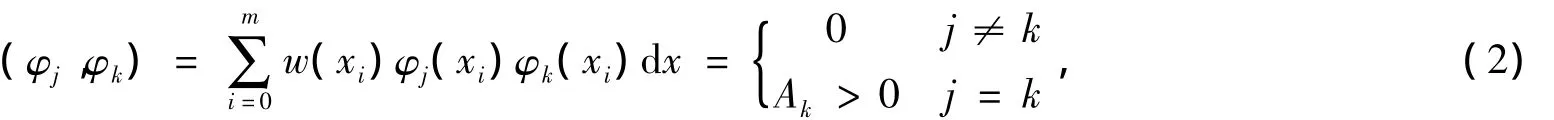
则称φ0(x)，φ1(x)，…，φn(x)是关于点集 {xi}(i=0，1，…，m)带权w(xi)(i=0，1，…，m)的正交函数族。特别地，当φ0(x)，φ1(x)，…，φn(x)均为多项式时，则称φ0(x)，φ1(x)，…，φn(x)是关于点集 {xi}(i=0，1，…，m)带权w(xi)(i=0，1，…，m)的正交多项式族。

3 最小二乘法

3.1 最小二乘法

定义3.1 若 φ0(x)，φ1(x)，…，φn(x)∈C［a，b］，如果a0φ0(x)+a1φ1(x)+…anφn(x)=0

当且仅当a0=a1=…an=0 时成立，则称 φ0(x)，φ1(x)，…，φn(x)在 ［a，b］上线性无关，称{φk(x)}(k=1，2，…，n)为［a，b］上的线性无关族。

最小二乘的一般提法:对于给于给定的一组数据 (xi，yi)(i=1，2，…，m)，要求在函数类 Θ=span{φ0(x)，φ1(x)，…，φn(x)}中找出一个函数y=s*(x)，使其加权平均和满足:

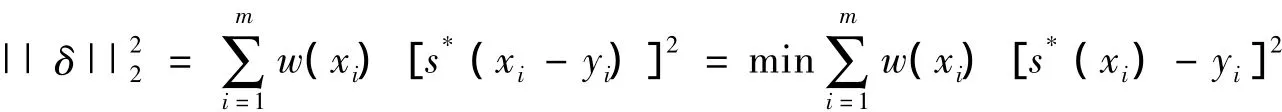
其中s*(x)=a0φ0(x)+a1φ1(x)+…anφn(x)，(n+1＜m)，这里 φ0(x)，φ1(x)，…，φn(x)∈C［a，b］是线性无关的函数族，w(x)是［a，b］上的权函数，w(xi)表示xi点处数据的重要程度。

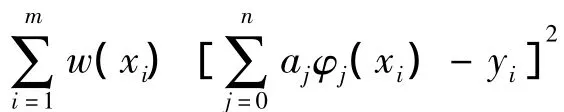
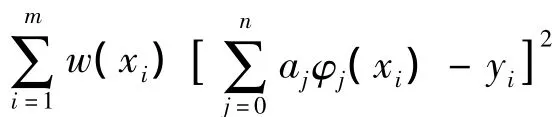
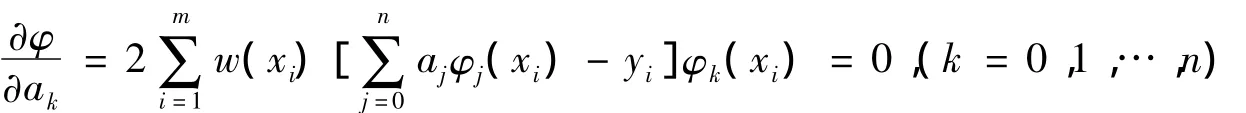
得:

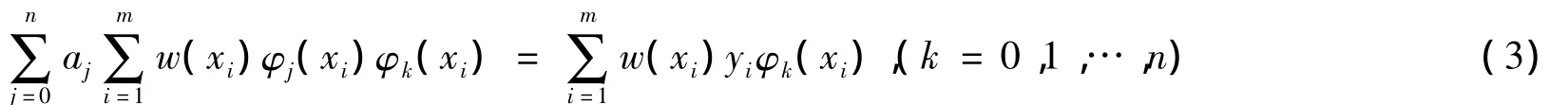
这是n+1个未知数n+1个方程的方程组，称为法方程式。

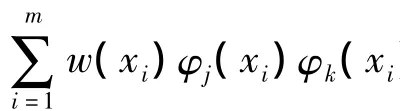
其中

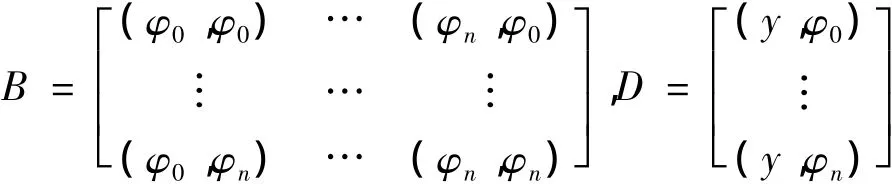
由上面的分析可知:用span{1，x，…xn}上的多项式拟合，首先需要解一个n+1的线性方程组。当n较大时，法方程的系数矩阵会出现病态。从系数矩阵B的形式来看，里面的元素都是内积。是否取得某些函数族，使得B的对非对角元素全变为0?如果有这样的函数族，那么方程组也容易解，并且病态也能够得到改善。

如果拟合函数在span{φ0，φ1，…，φn}上取，且{φk是正交函数族，则法方程为:

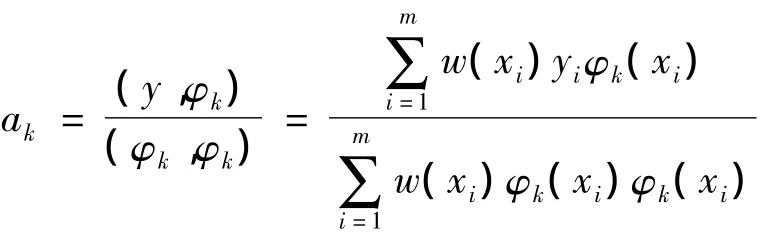
这样就不用解线性方程组了，完成以上工作就是如何构造正交函数族。

4 正交多项式曲线拟合

根据给定的结点(xi，yi)(i=0，1，…，m)及权函数w(xi)＞0，构造出带权正交多项式族{Pk(x)(n+1＜m)，用递推公式表示如下:

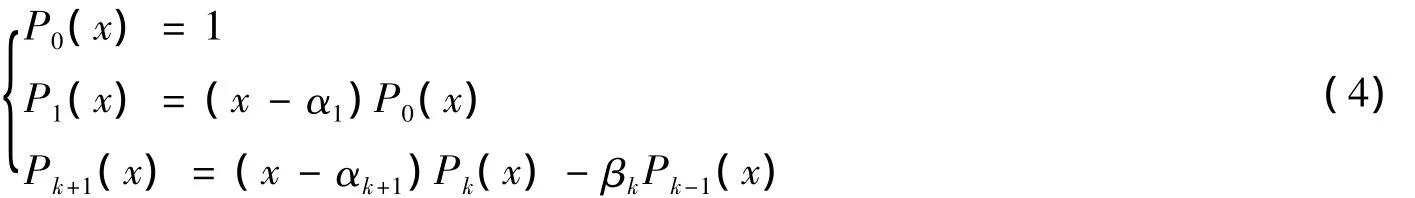
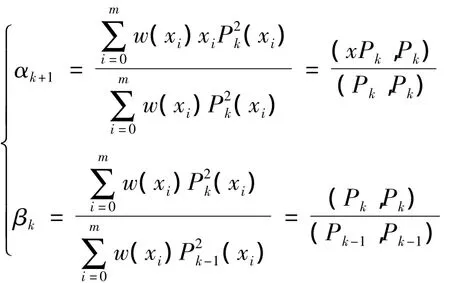
其中:这样给出的多项式{Pk(x)是正交的。

4.1 形如y=ax2+bx+c的曲线拟合

y=ax2+bx+c的基函数为1，x，x2，它们是线性无关的所以必有最小二乘解。当用正交基函数时，也可以得到相同的结果。

例1

表1 实验数据

(1)用正交多项式求解:

设拟合曲线函数为:y=c0p0(x)+c1P1(x)+c2P2(x)，由公式(4)得:

所以拟合曲线:

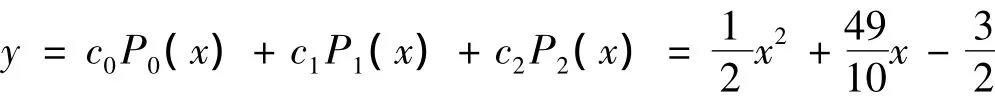
(2)最小二乘法求解:

设二次拟合多项式为y=ax2+bx+c，将数据带入公式(3)，得到法方程:

由上式可得:

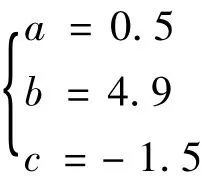
故所求的拟合曲线为:

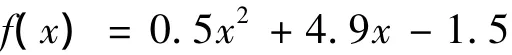
通过以上的数值模拟可以看出:用正交多项式和用一般的最小二乘法来拟合数据能够得到相同的结果。

4.2 形如y=ax2+c的曲线拟合

例2 已知实验数据如下

表2 实验数据

求形如y=ax2+c的经验公式。

1.用正交的方法:依据数据点构造正交基函数1和x2－1 065.4，设经验公式为:y=a1+a2(x2－1056.4)，利用公式(4)可得:

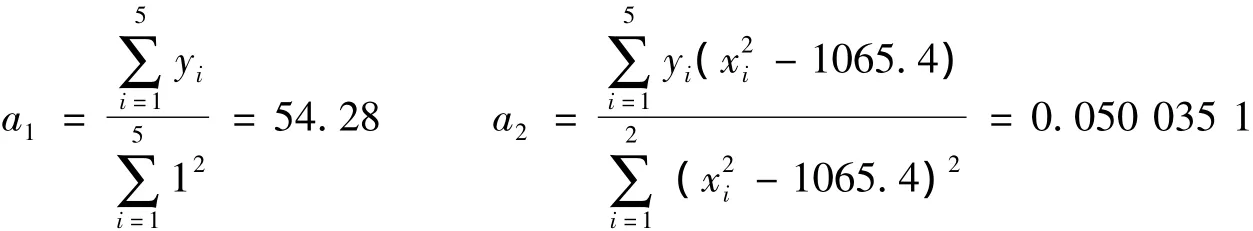
所以

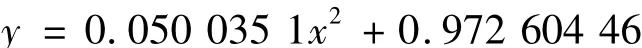
2.用一般最小二乘法:

将数据带入公式(3)得到法方程:

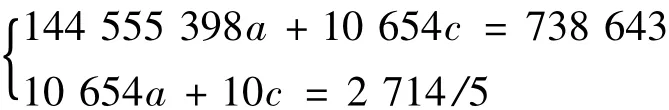
由方程组可得:

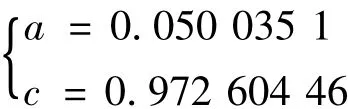
故所求的拟合曲线为y=0.0 500 351x2+0.972 604 46，其拟合曲线图形见(图1)。

图1 函数拟合曲线图

当缺少一个基函数时，我们能用最小二乘法直接进行拟合，但是用正交的方法，利用公式直接依据数据点构造新的正交基更简洁，计算的结果也是一样的。

4.3 数据缺项处理

假定采集了9个数据点，由于某种原因，缺失第5组y和第6组y数据，要求用一个函数把它表示出来，可以做如下处理:前4个数据和后3个数据用正交的方法拟合出2条曲线，然后在用过渡曲线把它们连接起来，形成一个分段函数，这样就能预测缺失点的数据值。

例3 已知实验数据如下:

表3 实验数据

求其经验公式F(x)，并估算F(0)，F(1)。

解前4组数据得到曲线记为f1(x)，后3组数据得到的曲线记为f2(x)，由于数据的散点图的变化趋势与二次多项式很接近，所以选取基函数1，x，x2，经计算可得:

因为拟合曲线点不在曲线上，取新的点(－0.8，16.905 8)，则由2个点上的函数值和导数值可得2条过渡曲线，设过渡曲线:g(x)=ax2+bx+c。

当选取点 (－0.8，16.905 8)导数值及函数值和点 (1.5，4.17)，可得g1(x):

当选取点 (－0.8，16.905 8)和点 (1.5，4.17)及它的导数值，可得g2(x):

拟合曲线F(x)的图形见(图2)和(图3)。

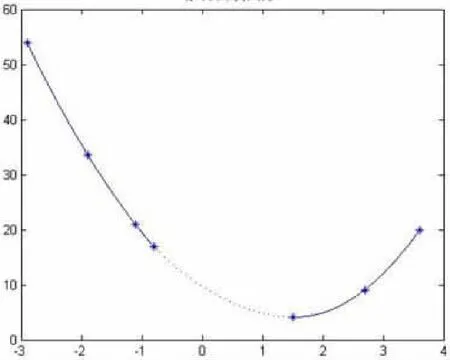
图2 拟合曲线

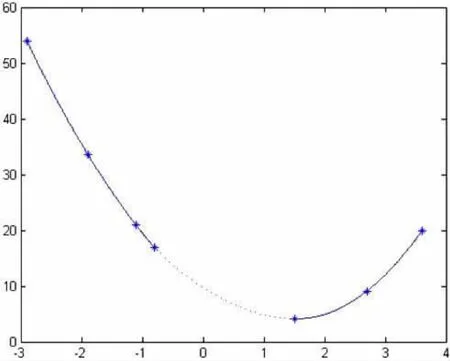
图3 拟合曲线

可以预测

从中可以选取一个合适的数值，选取的原则是预测点与光滑拼接点距离大小，选取距离小的函数，由此得到:F(0)=8.790 1和F(1)=9.080 2，原始数据见表4。

表4 原始实验数据

比较可以看出:预测的数据值和测量的数据值非常接近。

5 结论及展望

通过对一般多项式拟合数据的基础理论分析讨论，发现法方程组往往是病态的，并且计算不稳定，而选用正交多项式作为拟合的工具可以有效的避免病态问题，而且能够得到与一般多项式拟合相同的结果。另外，由于在工程实践中获得的实验数据常常是不完备的，本文主要针对一元原始数据缺失的拟合问题，提出采用曲线拼接的思想和方法，以满足一定光滑度的分段曲线来进行数据的拟合，实现对缺失数据的预测，其预测结果表明该方法切实可行。对于能否应用该思想处理多元数据缺失的问题将是今后讨论的重点。

［1］衣光臻.MATLAB曲线拟合工具箱在风机实验数据处理上的应用［J］.潍坊学院学报，2007，(2):30.

［2］李庆扬，王能超，易大义.数值分析［M］.北京:清华大学出版社，2001.

［3］任玉杰.数值分析及其Matlab实现［M］.北京:高等教育出版社，2007，3.

［4］李庆扬.数值分析基础教程［M］.北京:高等教育出版社，2001.5.

［5］王仁宏，李崇君，朱春钢.计算几何教程［M］.北京:科学出版社，2008.

［6］陈森，苏杰南.正交多项式的应用［J］.广西农林大学大学出版社.1997.

［7］Wang R.H，Chang J.C.A Kind of Bivariate Spline Space Over Rectangular Partition and Pure Bending of Thin Plate［J］.Applied Mathematics and Mechanics，2007，28(7)，963-971.

［8］Geronimo J.Scattering theory and matrix orthogonal polynomials on the real line［J］.Circuits Systems Signal Process，1982，25(3)，143-155.

［9］Chihara T.S.An Introduction to Orthogonal Polynomials［J］.Gordon and Breach，New York，1978.

［10］Wang R.H，Chang J.C.The Mechanical Background of Bivariate Spline Space S31［J］.Journal of Information and Computational Science，2007，4(1)，299-307.

［11］Chang J.C，Wang Z，Yang A.M.Construction of Transition Curve Between Nonadjacent Cubic T － B Spline Curves［C］.Lecture Notes in Computer Science，2010，(1)，454-461.