基于CS-ROMP算法的超宽带信道估计

杨 剑,蒋 挺,赵成林,周 正

(北京邮电大学泛网无线通信教育部重点实验室,北京100876)

0 引言

UWB是近年来通信领域兴起的一种无线通信技术,在无线通信系统中的应用越来越多,可以与现有窄带系统共存。但是为了在接收机中有效捕获多径信号的能量,超宽带系统要解决信道估计的问题,因此信道估计也成为超宽带系统研究中的一个热点。

近年来出现的压缩感知理论,能够对稀疏信号以低于奈奎斯特采样速率进行随机采样和重构。在利用压缩感知对超宽带系统进行信道估计时,信号重构算法对于恢复性能有着重要的影响。这里研究了正则正交匹配追踪算法在UWB系统信道估计中的应用。ROMP算法对于只需恢复一组最大径时的UWB信道估计很有益。最后与近似最优的DS算法进行对比,综合分析了ROMP算法和DS算法之间的性能。

1 压缩感知及系统模型

1.1 压缩感知

压缩感知理论是一种在采样的同时实现压缩目的的理论框架,其直接对信号进行较少采样得到信号的压缩表示,且不经过进行N次采样的中间阶段,从而在节约采样和传输成本的情况下,达到了采样的同时进行压缩的目的。其实现过程主要涉及信号的稀疏表示、观测矩阵的设计以及信号重构等3个问题,其压缩采样过程如图1所示[1]。

图1 压缩感知理论框架

1.2 UWB通信系统模型

在UWB系统的信道估计过程中,接收信号可以表示为:

<1)，且各件产品是否为不合格品相互独立．

式中,y为接收信号;S由Nx+N-1个已知符号(训练序列)组成;h=[h[0],h[1],…,h[N-1]]T,表示N×1的信道脉冲响应,其减采样后得到的观测点数是M,即仅仅有M个非零元素具有稀疏性;v为噪声[2]。

UWB信道是稀疏信道,时域的高分辨率使接收信号中多径交叠较少发生。在接收机和发射机严格同步的情况下,以发送UWB信号脉冲宽度为间隔对接收的符号进行采样,即对UWB多径信号的每一径只采样一个点,则可得到符合奈奎斯特采样准则的信道冲激响应h。压缩感知对h减采样后重构得到信道冲激响应的估计值^h。为了使接收机直接实现低于奈奎斯特速率的低速采样,接收机的观测矩阵可以由发射端的随机滤波器和接收端减采样联合实现。得到信道估计结果后,取部分较大径的估计值构造RAKE接收机。为了对抗噪声,训练序列采用重复编码,取估计结果的平均值作为信道估计结果[3]。基于CS的UWB信道估计框图如图2所示。

图2 基于CS的UWB信道估计

2 基于CS-ROMP的UWB信道估计

2.1 CS-ROMP在UWB信道估计中的应用

在压缩感知的信号重构阶段,有许多种不同的信号重构算法,这里将ROMP算法应用于UWB系统的信道估计。ROMP是OMP基础上发展而来,其和OMP的不同仅在于识别阶段:在识别阶段,OMP在每次迭代中仅增加一个索引号到索引集 Λl中,而ROMP在每次迭代中增加K个索引号到索引集Λl中。核心算法步骤为[4]:

输入:观测向量h∈RN,稀疏度K;

输出:索引集 Λ⊂{1,…,d},重构向量 ^v=y;

初始化:设置索引集 Λ=Φ,残差r=h。重复以下步骤K次或者直到|Λ|≥2K;

识别过程:在观测向量u=Φ*r中选择K个最大非零值组成索引集J,或者在非零值数目小于n的时候,由所有非零值组成索引集J;

正则化:使得所有的子集J0⊂J,在所有i,j∈J0的时候都具有可比较即相差不是太大的幅度|u(i)|≤2|u(j)|,选择具有最大能量‖u|J0‖2的索引集作为J0;

更新:增加子集J0到索引集:Λ←Λ∪J0中,更新残差;

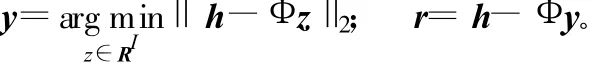
当满足迭代次数大于K或者索引集数目大于2K的时候,停止迭代,否则继续迭代。ROMP算法结合了l1范数稳定性和贪婪算法快速性之间的优势,在每次迭代之前对观测向量进行排序,保证了每次迭代的最优性。

IEEE802.15.4a是稀疏信道,可以应用压缩感知进行信道估计。在接收的UWB多径信号中,少量的最大径集中了大部分能量。为了降低信道估计的复杂性,只需对少数几个最大的径进行估计[5]。这里对信道的分析仅限于实值信道,不涉及复值信道的估计。

在ROMP算法中,每次迭代对观测向量u=Φ*r进行排序后选取K个最大值。在UWB信道估计中,目标是估计少数几个最大径的参数,集中了UWB信号85%能量的多径个数可以看作ROMP算法中的稀疏度K。因此将ROMP用于UWB信道估计的过程中更能有效重构。

2.2 DS(Dantzig Selector)算法

在压缩感知重构的过程中,DS算法在含噪声的信号恢复上有着近似最优的性能,因此被应用在信道估计中。这里将对比ROMP算法和DS算法的信道估计性能。DS算法是基于l1范数解决凸优化的算法,被看作是应对含噪声稀疏信号的近似最优的重构算法,对于稀疏信号和近似稀疏的信号重构误差的范围是可以判断的。DS算法的描述如下[6]:

假定 θ∈CΡ是一个未知但是可以判断的信号,在具有噪声的情况下,Ψ θ+η=r∈Cn,其中投影基Ψ是一个n×p的矩阵,其列具有单位l2范数的特征。复杂的加性高斯白噪声向量 η服从CN(0n,σ2In)分布。在 δ2S＜1/3的情况下,Ψ∈RIP(2S,δ2S),同时在a≥0的情况下,选择 λ=然后可以通过解决如下优化问题来估计 θDS:

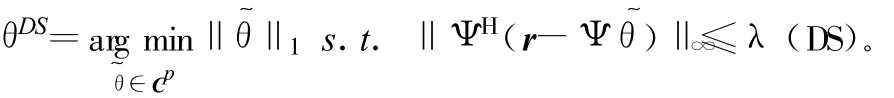
式中,

3 仿真场景及结果

3.1 仿真场景

这里使用MATLAB平台进行仿真,通过仿真对比ROMP算法和DS算法在信道估计中的性能。利用IEEE802.15.4a的信道脉冲响应h,总共有N个序列,其中有M个非零序列。对于信道实现,使用系统误码率性能来对信道的实现进行估计。采用BPSK调制,s[n]=±1。通过对大量信道实现的仿真遍历,可以获得信道估计的均方根误差曲线。

按系统模型构建系统,信道模型采用IEEE802.15.4a信道模型。分别得到在LOS信道和NLOS信道情况下,ROMP和DS算法在信道估计中的系统误码率情况。仿真中设定最大时延扩展为100 ns,采样率设为M/N=0.5,采用200个IEEE802.15.4a模型的信道冲激响应来统计信道估计的误差,通过‖^h-h‖/‖h‖来计算均方根误差。假定接收机需要估计70个多径的值,设定ROMP算法中输入信号的稀疏度K=70。

3.2 仿真结果及分析

图3显示了CS-ROMP在信噪比为20 dB时对一个信道响应实现的估计情况。由图3可以看出,ROMP估计的信道响应与真实信道响应中的较大径有较好符合。其中横坐标表示UWB脉冲信号出现时间,纵坐标表示原始信号脉冲幅度和经ROMP算法后恢复信号脉冲幅度。采用ROMP算法和DS算法在LOS信道和NLOS信道下进行信道估计的误码率曲线如图4和图5所示。

图3 原始信道冲激响应和经ROMP算法重构的信道响应

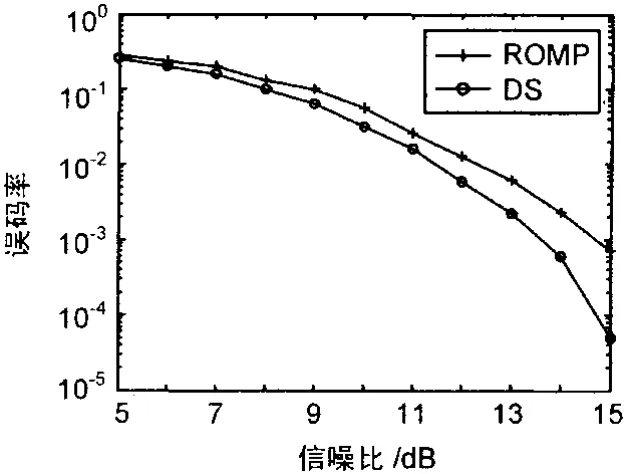
图4 LOS信道下的BER曲线

图5 NLOS信道下的BER曲线

通过图4和图5的对比可以看出,对于稀疏信道的估计,ROMP在LOS信道下的信道估计性能好于NLOS信道的情况,这是因为NLOS信道的多径比LOS信道密集很多,而且相比LOS信道,NLOS信道的多径之间增益相差不明显。为了使RAKE接收机具有适中的复杂度,仿真构造具有30个RAKE指的接收机,即取信道估计结果 ^h的最大30径构造RAKE接收机。训练序列的个数为1,训练序列和数据符号都采用了脉冲UWB系统中常用的重复编码策略,重复编码个数为10。仿真中,发送数据符号为20 000个。

通过图4和图5可以看出,ROMP算法和DS算法2种估计方法在UWB信道估计系统中的BER有所差异,在信噪比较低的情况下,ROMP算法做信道估计的系统误码率性能接近于DS算法做信道估计的系统误码率性能,在高信噪比情况下,DS算法性能好于 ROMP算法,而在实际UWB系统中,一般UWB信道的SNR比较低,因此在UWB信道估计的应用场景中,ROMP算法应用于基于压缩感知的超宽带信道估计系统的BER性能接近于DS算法。而对于同种信道下的估计,ROMP算法执行一次的运算时间是0.38 s,DS算法执行一次的运算时间是1.2 s,ROMP算法的计算复杂度远低于DS算法。综合考虑,ROMP算法在基于压缩感知的超宽带信道估计系统中具有较好的综合性能。

4 结束语

上述研究了基于压缩感知ROMP算法的超宽带系统信道估计,分别分析了在IEEE802.15.4a的LOS信道和NLOS信道中,ROMP和DS两种信号重构算法在信道估计中的性能。综合分析,ROMP在应用于超宽带系统估计中,具有较好性能。未来的研究工作包括ROMP在收敛速度与UWB信道估计之间的理论分析。

[1]石光明,刘丹华,高大化,等.压缩感知理论及其研究进展[J].电子学报,2009(5):1070-1081.

[2]FRIEDLANDER B.Random Projections for Sparse Channel Estimation and Equalization[C].SignalsSystemsand Computers,ACSSC'06.Fortieth Asilomar Conference,2006:453-457.

[3]ZHANG P,HU Z,QIU R C,et al.A CompressedSensing Based Ultra-wideband Communication System[C].IEEE International Conference on Communications,2009:214-226.

[4]NEEDELLD,VERSHYNIN R.SignalRecoveryFrom Incomplete and Inaccurate Measurements ViaRegularized Orthogonal Matching Pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310-316.

[5]PAREDES J L,ARCE G R,WANG Zhong-min.Ultra-WidebandCompressed Sensing:Channel Estimation[J].IEEE Journal of Selected Topics in Signal Processing,2007,1(3):383-394.

[6]BAJWA W U,HAUPT J,SAYEED A M,et al.Compressed Channel Sensing:A New Approach toEstimatingSparse Multipath Channels[J].Proceedings of the IEEE ,2010,98(6):1058-1076.

[7]CANDES E j,TAO T.The Dantzig Selector:Statistical Estimation when p is much Larger than n[J].Ann.Stat.,2007,35(6):2313-2351.

[8]TIBSHIR ANI R.Regression Shrinkage and Selection via the Lasso[J].Proceedings of the IEEE,1996,58(1):267-288.