某炮塔数字伺服控制系统误差分析

王永珍，王星民

(国营第785厂，山西太原 030024)

0 引言

任何一个实际的数字伺服控制系统，在满足系统稳定的前提下，总存在一定的误差。数字伺服系统在运行过程中的误差是多种多样的，但归结起来，误差主要源于元件误差、原理误差(系统误差)以及环境变化引起的误差［1］。

数字伺服系统由各种各样控制元件组成，如测量元件、执行元件等，而每种元件都有自身的误差。由于元件在系统结构中所处的位置不同，其本身的误差对系统误差影响程度也不同。

原理误差是指在控制机理方面必然产生的误差，它与系统的结构及控制作用的性质有关。原理误差分为确定型和随机型两类;确定型的原理误差就是在确定的输入信号和扰动作用产生的误差，而随机型的原理误差则是在随机输入和随机扰动下系统产生的误差。

环境的变化，例如温度、振动、冲击等的变化而使系统产生误差。

1 数字伺服控制系统误差的一般分析方法

在分析系统误差时，假定系统的结构是已知的。一个确定系统能传递和转化有效的控制信息，也能传递和转化干扰信息。如果把系统内部各元件的误差看成干扰信息，那么，它对系统精度的影响也就不难分析了。

在讨论系统的各种误差的定量分析和计算之前，首先来讨论一下本系统各环节对输入信号、干扰信号引起的误差传递和归化。设如图1所示结构的系统，输入为R(S)，输入干扰噪声为N0(S)，输出为C(S)，误差为E(S)，各级的等效扰动信号分别为N1(S)、N2(S)、N3(S)。因为对单位反馈系统而言，总的误差就是 R(S)、N1(S)、N2(S)、N3(S)所引起的误差归化到E(S)点上的总和。

图1 数字伺服控制系统框图

如果各量均为确定函数，那么可以用拉式转换归化:

如果系统中各变量是随机变量，而各变量相互独立，则可用统计理论来处理。设它们的功率谱分别为SR(ω)、SN0

实际上，系统的输入和扰动会有确定性函数和随机变量同时施加于其上。那么可以把它们分别进行计算和分析，误差是某时刻的确定于某个随机变量之和。在工程实际中因为每个干扰信号甚至输入信号引起的误差很小(可以取专门的措施来抑制某个比较严重的干扰)，同时又可以假定它们各自独立，因此认为误差向量是满足高斯分布的随机过程，这样式(2)就更有用处了。计算时，先算出均值，再算出方差σ，整个误差的概率分布函数就确定了，把误差待定为3σ，系统就有99.73%的概率分布达到了精度，需要指出的是，以上分析和处理有普遍的适用性。

对于非单位反馈系统，可以转化为单位反馈系统来处理;对于调节系统，实际上就是输入为常值或阶段变化的系统，以上的分析也适用。

在上面分析的各级干扰信号方面，没有规定是什么样的干扰。实际上，每个环节，包括测量、放大执行元件的误差都可以计算到它的输出端，作为对系统的干扰处理。对于多回路系统，可以从内环算起，等效为图1所示结构的单回路系统。每个回路的误差折算到输入(或输出)端作为某个干扰ni(t)［2］。

从以上的分析可以看到，图1所示的串级系统本身就具有抑制干扰的能力，而其干扰部位越靠近输出端C(S)，抑制能力越强。系统抑制前级的干扰能力一般比后级差，这就是一般数字伺服控制器系统要求测量元件和前级信号放大器精度高的原因所在。

2 系统元件误差分析

本炮塔数字伺服控制系统的元件主要包括执行元件、测量元件等。

2.1 执行元件的误差

执行元件主要由俯仰轴系和方位轴系组成。

2.1.1 俯仰轴系误差

(1)俯仰轴于垂直轴的不垂直度误差σ1

设计要求IT6级精度。方位座圈径向跳动是0.1 mm，高度取1.4 m，则如图2工作所示的几何关系。

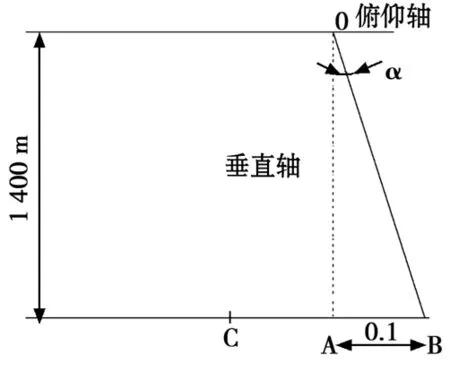
图2 俯仰轴与垂直轴的几何关系图

α =14.7 〞

即:σ =14.7 〞

(2)偏移量σ2

主要是由支承俯仰轴的轴承内环不同心引起的。不同心度的最大值为0.2 mm，轴心跨轴为820 mm～940 mm之间，按反余弦分布，偏移的均方差根为 σ2=45″。考虑所有在俯仰轴上的设备不一致性为0.8 mm，即:σ2=59″。

(3)随机偏移量为σ3

由于运动产生惯性力，这次误差最大不超过100″，即σ3=100″。

(4)计算结果

由上述计算可见三项误差为:

2.1.2 方位轴系误差

根据实践经验，方位误差为俯仰误差的50%。

即 σ方=0.975'=0.29 mrad

2.1.3 俯仰和方位轴系总误差

综合俯仰和方位两项综合误差，加上机架安装误差σ安=1.3'。则均方差为:

2.1.4 减小执行元件误差的方法

(1)执行元件属传动动力链范畴，其误差(主要指末级误差)在系统闭环外。该误差可通过测量经软件或调整环节弥补。

(2)本系统轴系末级传动比i俯仰=8，i方位=12。真正

2.2 测量元件(即位置传感器)的误差

数字伺服控制系统中的测量元件对系统精度的影响是直接的，因为一般反馈用测量元件来测量被控对象或过程与给定输入的差值，然后将其放大后再驱动直接机构去调节。可见测量元件的误差是系统中最直接的误差。一般来说，测量元件的误差分量是很重的，至于反馈所包围回路中的各种放大、执行等元件的误差或环境变化而引起的误差，一般都会得到有效地抑制。

(1)位置传感器的误差分析

本系统中位置传感器选用德国海德汉公司生产的绝对式光电编码器(型号为ROC425)，其最大误差σ生产≤20″，根据经验，其安装误差σ安装≤1.3'，则均方差为:

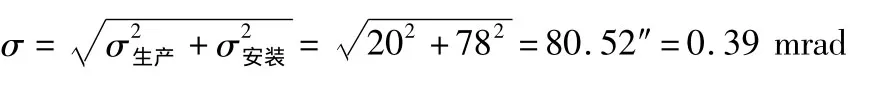
(2)减少位置传感器误差的方法

减小安装误差，适当提高传感器分辨率。

3 原理误差分析

其原理误差分为确定型和随机型两类。

3.1 确定型原理误差

3.1.1 建模误差

由于本系统设计为带前馈补偿的Ⅱ阶无差系统，加之建模误差对系统影响较小，可忽略。

3.1.2 计算机有限字长产生的量化误差

由于数字伺服控制系统0～360°用16位字长表示，即量化单位为:

所以量化误差为0.1 mrad。

3.2 随机型原理误差

本系统在跟踪输入信号运动的过程中要克服各种干扰，其中很多为随机干扰。对于随机噪声干扰，可用统计理论来计算该干扰引起的误差的统计值。随机干扰值多种多样，全面分析比较困难，一般在设计中具体问题具体分析。根据实际经验，一般来说随机型原理误差在系统误差中所占比重不超过10%。

4 环境变化引起的误差分析

4.1 振动冲击引起的误差

由于炮塔的质量大，固有频率低，振动冲击引起的误差可忽略。

4.2 温度变化引起的误差

由于转塔结构材料均选用铝或钢，其对温度不敏感，控制设备的元器件均选用宽温器件，加之系统的PID调节，所以，由温度引起的误差可忽略。

5 误差分析统计

表1是本炮塔误差分析统计，可供数字伺服控制系统分析参考使用。

6 结论

本文针对数字伺服控制系统运行过程的元件误差、原理误差、环境变化引起的误差进行了分析，并将其误差分析方法实际应用于某炮塔数字伺服控制系统误差分析中，给出本炮塔的误差分析统计，实践证明该方法行之有效，为数字伺服控制系统的设计分析提供了指导。

表1 炮塔误差分析统计

［1］卢志刚，吴杰，吴潮.数字伺服控制系统与设计［M］.北京:机械工业出版社，2007.

［2］胡祐德，马东升，张莉松.伺服系统原理与设计［M］.北京:北京理工大学出版社，2000.