基于EM算法的SAI图像插值改进技术

侯翠翠，干宗良

(南京邮电大学通信与信息工程学院，江苏南京 210003)

0 引言

图像插值是利用已知邻近像素点的灰度值来产生未知像素点的灰度值，从而再生出具有更高分辨率的图像。图像插值能够有效地提高图像的分辨率，它已经成为图像领域中的一项热门课题，被广泛地应用到军事、航空、医学、通讯、气象、遥感、动画制作、电影合成等领域。目前提出了很多图像插值的方法。传统的插值技术［1，2］，如线性插值、双立方插值、样条插值。虽然复杂度低，计算速度快，但易产生锯齿、模糊以及振铃效应等。基于边缘的插值技术［3］，可提高图像的边缘清晰度，但存在边缘偏离的现象，放大倍数越大，偏离越严重。基于区域的插值技术［4］，在主观和客观上，都能获得较好的图像质量。

在众多的插值算法中，SAI算法［5］获得了比较好的插值效果，它采用最小二乘法优化PAR模型参数。本文提出了一种新的PAR模型参数优化方法:基于EM算法的PAR模型参数优化。本文算法的核心思想:E步用已知的像素值和估计出的PAR模型参数估计插入值;M步用已知的像素值和E步估计出的插值对PAR模型参数估计值修正。相比SAI算法，本文算法获得了更好的图像边缘以及较高的峰值信噪比。

1 SAI算法的基本理论

SAI算法的关键是解决3个最优化问题，即PAR模型参数矢量 a=(a1，a2，a3，a4)，b=(b1，b2，b3，b4)的最优化以及图像插入值的最优化。

PAR模型参数a、b采用最小二乘法优化，即:

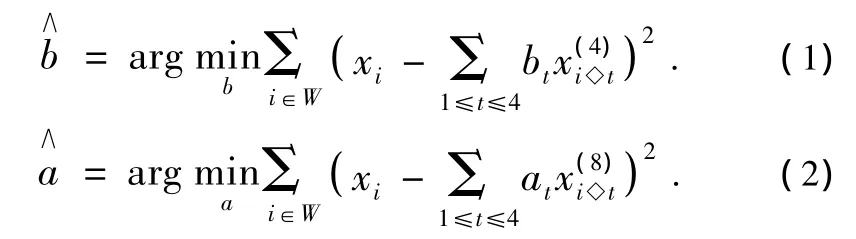
其中，W是正八角形的窗。

然后，通过最小化式J(λ)估计出图像插入值。即:

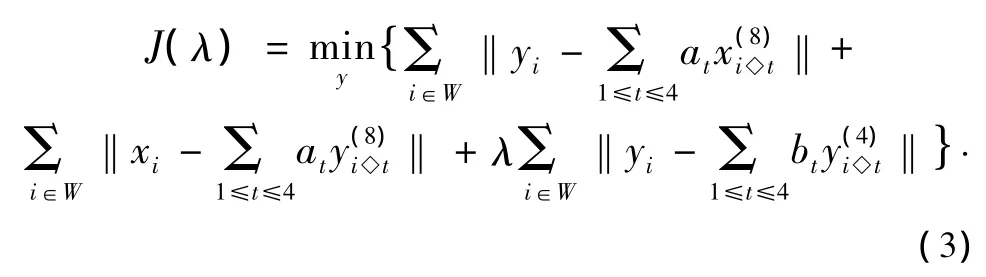
其中，λ一般取0.5。式(1)－(3)中，符号表示的意义如图1所示。

图1 PAR模型参数a，b及像素位置的配置

2 基于EM算法的SAI插值算法

2.1 EM算法简介

EM算法是一种基于数据添加思想的迭代算法，是Demmpeter等人1977年提出求参数极大似然估计的一种方法，它可以从非完整数据中计算出参数的最大似然估计。它广泛地应用于处理缺损数据，截尾数据，带有讨厌资料等的非完整数据。

EM算法的每次迭代过程执行两步:E步(Expectation step，期望步)，在给定观测数据和前一次迭代参数估计的情况下，极大化缺失数据对应的对数似然函数的条件期望，从而估计出缺失数据;M步(Maximization step，最大化步)，在给定观测数据和E步缺失数据估计的情况下，通过极大化对数似然函数以确定参数的值，并用于下一次的迭代。算法在E步和M步间反复进行，直到算法收敛。

2.2 基于EM算法的模型参数估计

由式(1)可知，SAI算法中，模型参数b是由 xi和它的4个相邻像素估计所得，它和式(3)中的模型参数b是同方向且等距离的，如图2(a)所示。但由于图像采样后的协方差可能改变，所以直接将式(1)估计出的b用于式(3)可能导致数据的过拟合，使插值图像产生错误的边缘。因此，本文将用估计出的图像插入值yi和它的4个相邻像素对式(1)中的模型参数估计值进行修正。则此时模型参数b的估计可表示为:

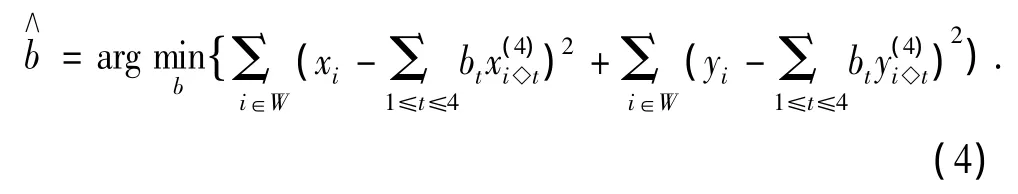
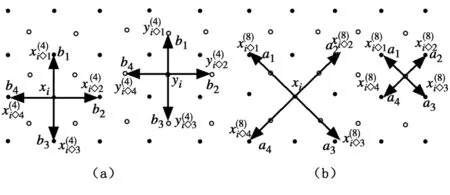
图2 式(1)和式(3)中模型参数a，b的比较

同理，式(2)中模型参数估计也可用图像的插入值yi和它的4个相邻像素来修正。同时，式(2)的模型参数a的估计还存在一个问题:式(2)中xi和它的相邻像素的距离是式(3)中yi和它的相邻像素距离的2倍，如图2(b)所示。由于不同间隔距离的像素之间的相关性不一定相一致，所以将式(2)的估计值用于式(3)中插入值的估计，估计出的插入值难免存在误差。针对上述问题，本文将用估计出的图像插入值yi和再次对式(2)中的估计值进行修正。则此时模型参数a的估计可表示为:

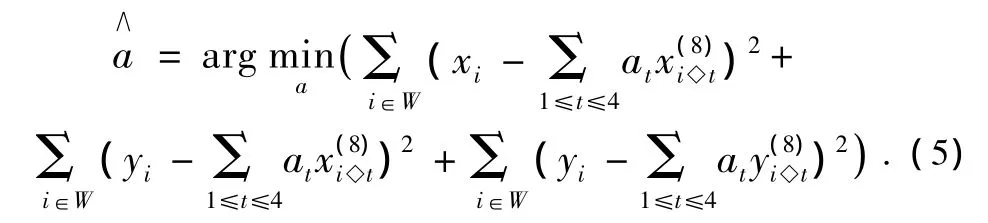
式(3)－式(5)中，低分辨率图像像素 xi已知，插入的像素yi和PAR模型参数a，b均未知，该问题可用EM算法解决。在统计模型中，把插入的像素值yi看作是缺失数据，则yi和xi可组成完整数据，模型参数a和b可作为未知参数，希望在丢失数据yi的情况下得到模型参数a和b的最大似然估计。则EM的主要思想如下:

(3)M步骤:E步骤获得的插入值yi和低分辨率图像像素xi，通过计算式(4)和式(5)获得模型参数估计值

(4)重复E和M步骤，直至超过设定的迭代次数(一般取3次)，输出图像插入值yi。

2.3 算法的具体实施

取W是正八角形窗，则式(3)可以写成矩阵的形式:

其中，矩阵C、D在SAI算法中已经给出，向量y是窗中要插入的像素，仅取窗内最里面的像素。向量x是窗中的已知像素。

同样，式(4)和式(5)也可以表示为矩阵形式:

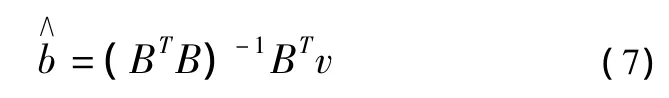
其中，矩阵B的第i(i=1，2，…，21)行是 xi的4个四方向的相邻像素和第i(i=22，23，…，33)行是 yi的4个四方向的相邻像素。向量v是窗中的已知像素 x1，x2，…，x21和y1，y2，…，y12.

其中，矩阵A的第i(i=1，2，…，21)行是 xi的4个八方向的相邻像素和第 i(i=22，23，…，33)行是 yi(i=1，2，…，12)的4个八方向的相邻像素 xi和第i(i=34，35，…，45)行是yi(i=1，2，…，12)的4个八方向的相邻像素 yi。向量 v是窗中的像素 x1，x2，…，x21和 y1，y2，…，y12。

如2.2所述，采用EM算法解式(6)－(8)。

上述仅介绍了第一步的插值过程，第二步插值与第一步插值唯一的不同处是，第二步的插入像素采用它的4个四方向的相邻xi像素或第一步插入的像素yi来估计。

3 实验结果及分析

本文采用图像 lena、boy、fish、mrit、flower作为测试图像，如图3所示。以双立方插值算法，SAI算法以及本文所提出的算法进行2倍插值实验对比。

图3 本文用到的测试图像

为观察图像放大后的细节，在lena、boy、fish测试图像中分别取尺寸为200×200的子图像作为观测图像，先对子图像进行2×2的下采样，然后分别用3种算法对下采样图像进行2×2插值，结果如图4所示。以lena的局部放大图像为例，双立方插值算法中lena的肩膀处存在严重的模糊及沿边缘方向的锯齿;相比于双立方插值，SAI算法能有效地减少图像边缘的模糊及沿边缘方向的锯齿，但仔细观察会发现，lena图像的肩膀边缘仍有模糊和细小的锯齿;相比于SAI算法，本文算法进一步减少了图像的模糊和锯齿效应，获得了更好的视觉效果。

图4 几幅图像的局部放大效果

为了测试算法的全局性能，计算插值图像的峰值信噪比，结果见表1，差值是本文算法比其它两种算法高出的峰值信噪比。从中可以看出，本文算法的峰值信噪比比双立方插值算法高0.17dB～1.89dB，比 SAI算法的峰值信躁比高0.10dB～0.37dB。这与实验结果所表现出的视觉效果是一致的。

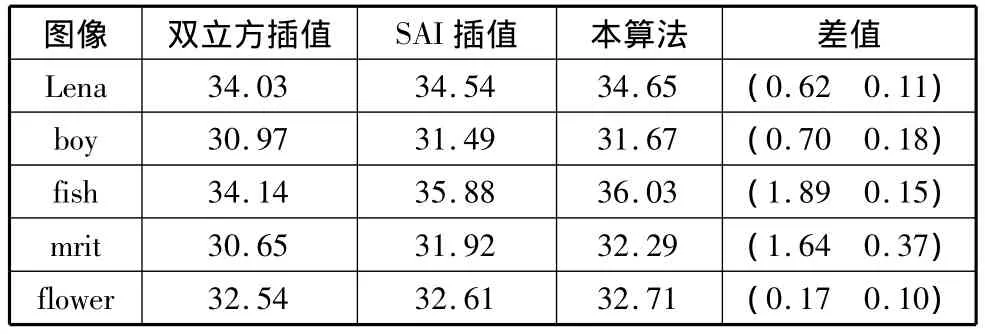
表1 3种插值算法的峰值信噪比

4 结束语

本文提出了一种基于EM算法的PAR模型参数优化算法。在E步利用估计出的PAR模型参数和已知的像素值估计出图像插入值，在M步利用E步估计的插入值和已知的像素值估计出模型参数。仿真结果表明，本文所提出算法获得了良好视觉效果和客观质量。

［1］Keys R G.Cubic Convolution Interpolation for Digital Image Processing［J］.IEEE Trans-actions on Acoustics，Speech and Signal Processing，1981，29(6):1153－1160.

［2］Hou H S，Andrews H C.Cubic Splines for Image Interpolation and Digital Filtering［J］.IEEE Transactions on A-coustics，Speech and Signal Processing，1978，26(6):508－517.

［3］Li X，Orchard M T.New Edge-Directed Interpolation［J］.IEEE Transactions on Image Processing，2001，10(10):1521－1527.

［4］王会鹏，周利莉，张杰.一种基于区域的双三次图像插值算法［J］.计算机工程，2010，36(19):216－218.

［5］Zhang X，Wu X.Image Interpolation by Adaptive 2-D Autoregressive Modeling and Soft Decision Estimation［J］.IEEE Transactions on Image Processing，2008，17(6):887－896.

［6］Wu X，Barthel E U，Zhang W.Piecewise 2D Autoregression for Predictive Image Codings［C］.Proceedings of IEEE InternationalConferenceon ImageProcessing，1998，3:901－904.