基于弹道计算的截断误差估计与补偿
2011-06-13陈红英李辉芬伍辉华
陈红英,李辉芬,伍辉华,何 晶,吴 君
(中国卫星海上测控部,江苏江阴214431)
0 引言
弹道测量数据事后处理的结果是作为型号试验的精度分析、评定和性能改进、提高的重要依据,不断改进测量数据处理方法和技术,提高弹道测量数据精度,对于提高海上测控水平和综合试验能力有重要意义。由于种种原因,外测系统的观测数据总含有随机误差,必须通过相应的平滑与滤波处理,以减小随机误差的影响。但当弹道变化的曲率较大时,速度和加速度参数变化剧烈,微分平滑公式的误差对计算结果的影响很大,会产生较大的截断误差。如何进行截断误差的补偿、提高弹道参数的精度是数据处理中面临的迫切问题。通过对截断误差补偿原理和方法的介绍,采用理论弹道补偿法对外弹道特征点前后数据进行了补偿计算,分析了对弹道参数进行截断误差补偿的有效性和可行性。
1 误差原理分析
运载火箭的飞行过程极其复杂,为了降低随机误差的影响,拟合多项式的阶数越低越好,观测数据的总平滑点数越多越好。为此,输入观测数据的真实信号要用低阶多项式来近似描述,这样又会造成严重“失真”,另外在一定的观测采样频率f下,参与平滑的观测点数越多,则总的平滑区间T=N◦h也越长,就需要用一个较高阶多项式来描述。采用曲线拟合平滑微分方法计算弹道参数不可避免地会有截断误差,对于位置和速度变化剧烈的弹道段,更是存在较大的截断误差。例如级间分离段、关机段和再入段等弹道曲率较大,这也是人们比较关注的弧段,为能正确反映目标飞行轨迹,得到精确的弹道参数,必须对其进行修正补偿。
根据弹道动态情况,实际数据误差特性和所需精度要求,对非关机点附近的主动段弹道、自由段弹道和再入段弹道,位置数据一般采用1阶或3阶中心平滑,速度数据采用2阶中心平滑,加速度数据采用3阶中心平滑比较合适。平滑区间则根据弹道动态各外测系统的观测数据采样率来决定。对于中心平滑,假设输入的观测数据序列为xi,i=-n,-n+1,…,0,…,n,并且记中心平滑后输出的中心点的估计值为于是输入观测数据与输出数据的关系为:

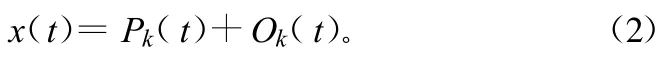
现将输入观测数据xi关于中点i=0做k阶泰勒展开,并用积分形式表示其余项,则

将输入观测数据的泰勒展开式代入中心平滑公式,那么滤波输出数据为:

由wi的性质可将式(4)变为:

式中,第1项为中心点i=0真实信号的L阶导数,而是中心平滑后输出的数据。可以看出和相等的充要条件是上式右边第2项为零,也就是只有输入观测数据的真实信号x(t)为k阶时间多项式,余项的滤波结果才能为零。或者说,x(t)是高于k阶的时间多项式,则中心点滤波后的就有误差。令
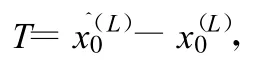
并称T为k阶多项式中心平滑的截断误差。
2 补偿方法
截断误差补偿方法常用理论弹道补偿法和外遥联合补偿法,另外还有截断误差函数补偿法。
2.1 理论弹道补偿法
假若有理论弹道数据X和,则事先可由理论弹道的坐标数据X用微分平滑方式计算出t时刻的速度值,再将t时刻的理论速度值X与做差,得到该时刻的截断误差估计量为处理时把作为实测数据微分得到的的补偿值,该方法称为理论弹道补偿法。对于加速度微分平滑也可按同样原理处理。但应注意的是,实际弹道与理论弹道是有差别的,必须把特征点对齐后,再由此向特征点前后进行相应的补偿。
2.2 外遥测联合补偿法
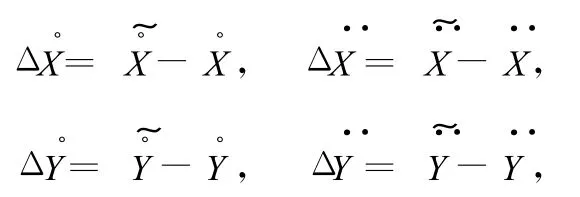
视为截断误差,加到对应的外测所得到的速度和加速度上进行补偿,该方法称为外遥测联合补偿法。具体计算步骤如下:
①由遥测过载参数nx、ny和程序俯仰角φ计算
③根据前述的原理得到对应量的截断误差补偿值。
2.3 函数补偿法
构造截断误差补偿函数Ri(n,p)。假设ti的速度真值为,微分值为对应的截断误差为Ri(n)。显然,截断误差与点数n有关。假设在同一时刻ti,取n=k,k+1,…k+L,则由微分公式可得一系列计算速度值和L均为正整数。于是有:

当采样间隔h确定后,截断误差随n的增大而增大,而同一时刻的是确定的常数。因此随n的增大而远离反之则接近在O-n坐标系中,以n为自变量,并用最小二乘拟合法求出拟合曲线Ri(n,p),其中p为曲线的阶数。即设

式中,待定常数ai在K、L、P给定时,由最小二乘法求得,并称Ri(n,p)为误差补偿函数,用它作为的近似值,相当于对的补偿。
3 应用效果分析
综合考虑上述3种截断误差补偿方法的优点和局限性,在短时间内采用理论弹道补偿法对外弹道测量数据进行误差补偿。
在测量船某型号任务R中,将理论弹道数据资料进行整理,并对火箭运行过程各特征点数据进行了截断误差的补偿,具体方法是利用理论时刻的加密弹道对实际特征点时刻前后若干点的弹道数据进行补偿,其中包括X、Y、Z方向的速度x◦和加速度x
¨处理数据,弹道倾角、偏角,切向、法向和侧向加速度等。根据理论弹道补偿法的原理,对齐特征点是补偿的重要步骤。
表1中列出了某型号任务R在特征点A时刻T(相对时1 100 s)X方向速度和加速度前后补偿结果的部分数据。

表1 特征点A时刻前后数据补偿情况
从表1中可以看出在特征点A附近补偿量数据变化激烈,补偿量明显变大。
由于速度数据采用2阶中心平滑,加速度数据采用3阶中心平滑,实战任务R中补偿前的数据做了平滑处理,而截断误差补偿后的特征点A和特征点B时刻X方向速度和加速度数据变化情况如图1和图2所示。
图中2条曲线分别为未做误差补偿和已做误差补偿的曲线,从图1和图2可以看出,任务时间段内整个曲线的变化趋势,在2个特征点时刻曲线发生明显跳变,通过对特征点时刻局部放大,可以更加清楚地看出补偿量的大小,这也验证了在特征点时刻截断误差较大的理论。
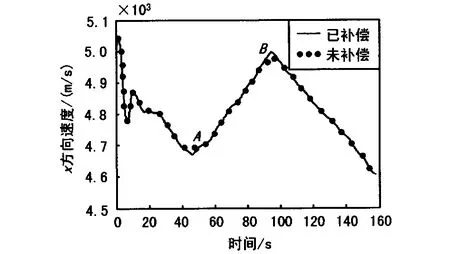
图1 各特征点时刻X方向速度截断误差补偿
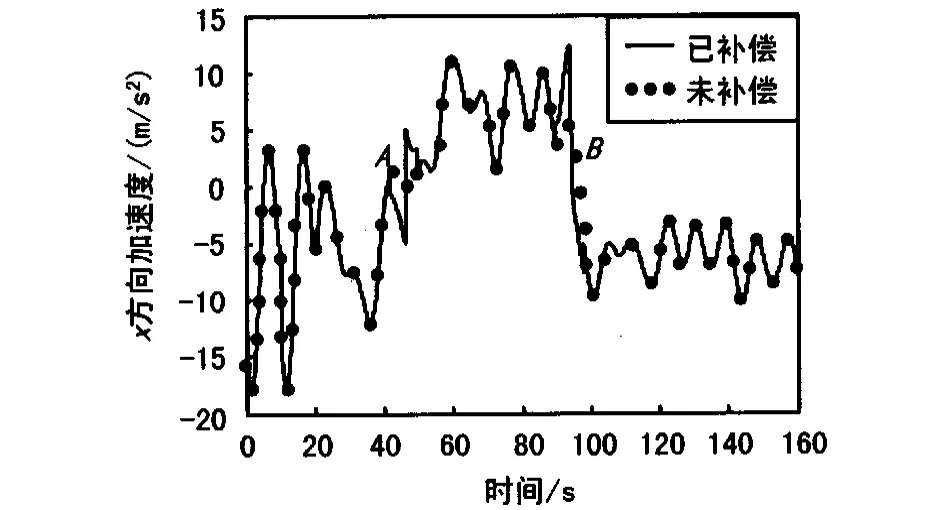
图2 各特征点时刻X方向加速度截断误差补偿
对火箭运行过程中位置和速度曲率较大的特征点参数进行误差补偿,真实地体现了目标的飞行轨迹,得到较为精确的弹道参数,证实了对特征点时刻参数作截断误差补偿的必要性。
4 结束语
采用理论弹道对速度和加速度等弹道参数进行截断误差补偿,取得了明显的效果,从计算的结果可以看出,在特征点利用理论弹道对参数进行截断误差补偿,其计算精度远远高于通过微分坐标求解的结果精度,该方法的成功运用大大提高了弹道参数的处理精度,为不断提高测量船海上测控任务数据处理方法和技术提供了重要依据,也被应用于测量船后续的各种任务中用于获取高精度的雷达等外测设备的弹道参数数据。
[1]刘利生.外弹道测量数据处理[M].北京:国防工业出版社,2002.
[2]张忠华,李晓勇.船载设备动态测量数据的建模与参数估计[J].无线电工程,2008,38(5):13-17.
[3]柴 敏.运载火箭外测弹道截断误差的洁化插值修正算法研究[J].航天控制.2009(5):10-14.
