Safety Model Comprehensive Judgement Application and Risk Evaluation System Research for Main Embankment of Yangtse Rive in Southern Jingzhou Zone of China

2011-06-13WANGYajun

浙江海洋大学学报(自然科学版) 2011年3期

WANG Ya-jun

（School of Naval Architecture and Civil Engineering of Zhejiang Ocean University,Zhoushan 316004,China）

The dominant factor over the whole dike system is the safety behaviour of dike body which holds on such roles as withstanding flood invasion,saving the proper living condition for the local citizen,carrying out the necessary safety monitoring on the dike section etc.When considering dike body characteristics as well as the exterior and interior facets over the dike body safety,therefore,the systematic peculiarity is also relevant to the dike body model.

With so many quantitative indexes on this model in addition to the ostensive fuzzy behaviour of porous medium[1-3],fuzzy comprehensive judgement system model would be implemented here.In order to practise instant management for the dike structure,for instance,picking out the most consistent section and the most inconsistent with normal section,ascertaining the normally safe dike section,basically safe dike section,partly safe section,unsafe dike section,the comparison between the target sections and normal section which shows the certain work-condition as well as superior safety,has been put into practice according to their various chasms with fuzzy comprehensive judgement and modification theory.

1 Formulation on Structural Model of Fuzzy Comprehensive Judgement System based on Analytic Hierarchy Process

1.1 Safety Evaluation Model on Dike Body

By virtue of this fact that dike body hierarchy characteristics has been interpreted largely in the reference[8],the researching key for systematic index choice and model ascertainment would been put closely on such facets as seepage deformation and porous medium mechanics quality.

When the dike section stress field and seepage field have been analyzed as the Fig.1 as well as Fig.2,the eventual structural model based on these deterministic indexes has been showed as the Fig.3.

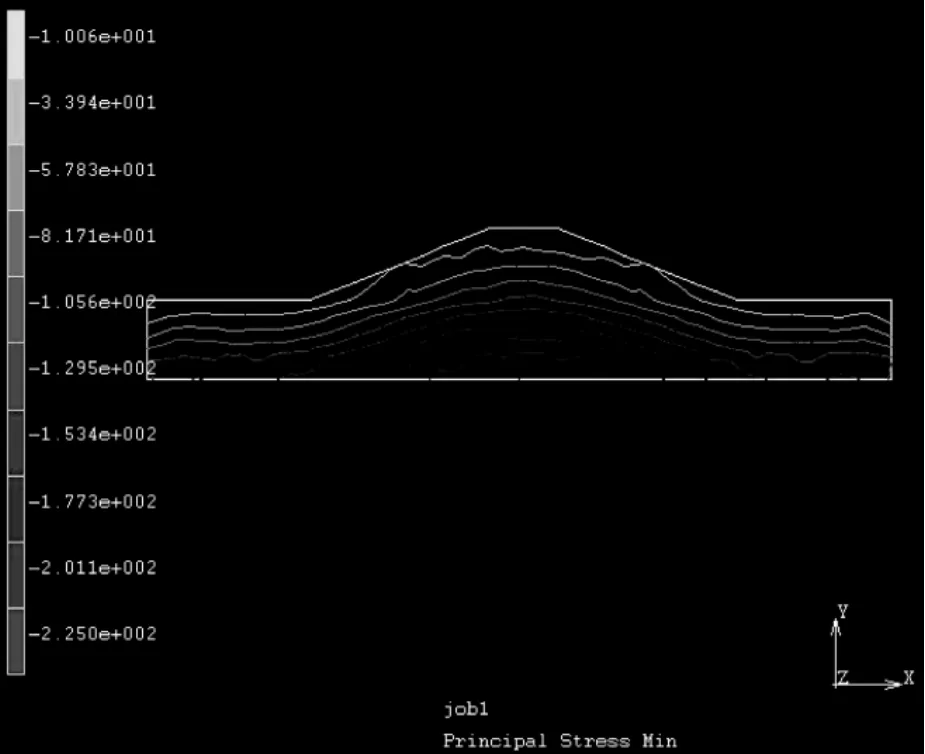
Fig.1 Dike stress field finite element method analysis

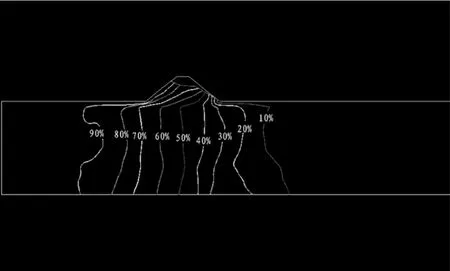
Fig.2 Dike seepage field finite element method analysis

1.2 AHP Model Algorithm

With the same hierarchy traits,the implementation for model judgement is initiated from the“controlling coverage”.It is given that the indexes group for any sub-coverage is the following:

the corresponding judgement criterion group is below:

Step 1:

As the counterpart for any sub-coverage of the “controlling coverage”,namely,Ai,all relevant indexes in the“decision coverage”are（j=1，2，…m）.When formulating the respective weight of indexesto sub-coveragejudgement matrixf sub-coverage Ai indexes grouprelative to judgement criterion group V={V1，V2，…Vk}astherefore,here lived is a fuzzy transformation as the following:

The model judgement consequence of sub-coverage Aiunder“controlling coverage”,so,comes into being as，relative to judgement criterion group V={V1，V2， … Vk}.The algorithm for other sub-coverage under“controlling coverage”as well as“intermediate coverage”could be realized by following suit way.

Step 2:

With the foregoing deduction,the ultimate implementation for model function,namely,the general judgement for model function could be realized.It is given that sub-coverage under“primary intermediate coverage”is Ai=（i=1，2，…n）,furthermore,its fuzzy comprehensive judgement result being（i=1，2，…n）.When stipulatingW1，W2，…Wn}as the weight group of all these sub-coverage A（ii=1，2，…n）under“primary intermediate coverage”relative to“general coverage”A,in addition tothen,is the judgement matrix (namely,fuzzy correlation matrix)[4]of judgement indexes group {A1，A2，…An}relative to judgement criterion group V={V1，V2，…Vk},and fuzzy transformation could be fabricated as the following:

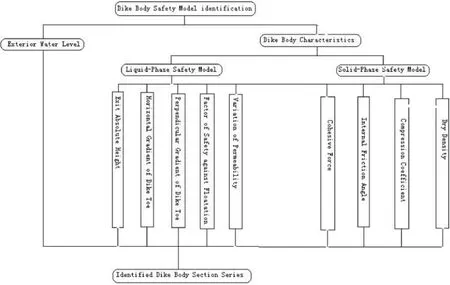
Fig.3 AHP structure on safety model of dyke body

Due to the maximal membership grade criterion,the subscript series ofis the general judgement for model target,namely,typical dike body section.

2 Safety Model Comprehensive Judgement on Dike Body Section of Yangtse Rive Main Dike in Southern Jingzhou Zone of China[5-6]

In order to certifying the structural model of dike body system based on porous medium characteristics,9 typical dike sections of Yangtse Rive Main Dike in Southern Jingzhou Zone of China are chosen into researching category.

2.1 Interpretation on Indexes Characteristics of Typical Dike Body Section of Yangtse Rive Main Dike in Southern Jingzhou Zone of China

This part is covered with the reference*1.At the same time,the generalization for indexes is a very onerous work because some indexes,seemingly quantitative,is factually qualitative that should embody somewhat subjective viewpoint which must consist with engineering objectivity as closely as possible.Furthermore,fuzzy clustering on judgement program with these deterministic indexes has to be carried out sometimes to find out the reaction of the model so that the appropriate adjustment could be offered.

2.2 Algorithm on Fuzzy Comprehensive Judgement

1)Determination on Judgement Criterion Group

During the implementation of hierarchy comprehensive judgement,there must live two theoretic ranges,the first being judgement indexes group U={U1，U2，…Um},the second being judgement criterion group V={V1，V2，…Vm}.With the reference[7-9],grade standardization for these indexes is showed as Tab.1 where,c、ωreferring to shearing strength indexes;av、ρstanding for compression coefficient and wet density of fill-stuff; Δh being exiting point group absolute height;J=、J┴standing for dyke-toe exiting gradient in horizontal direction and vertical direction; η being factor of safety against floatation;vk、H representing variation of permeability and exterior water level.

2)Membership Function and Fuzzy Correlation Matrix[10,11]

The key for every judgement index in fuzzy comprehensive judgement model is to fabricate its membership grade.In this paper,membership function is offered to avert the possibly redundant uncertainty such as de-dimensional transformation[12].

With sound reference of the relative engineering disciplines and local engineering back-ground,the normal fuzzy membership function,which could be adroit with the geo-engineering disciplines,has been chosen to take on the fuzzy comprehensive judgement model simulation.

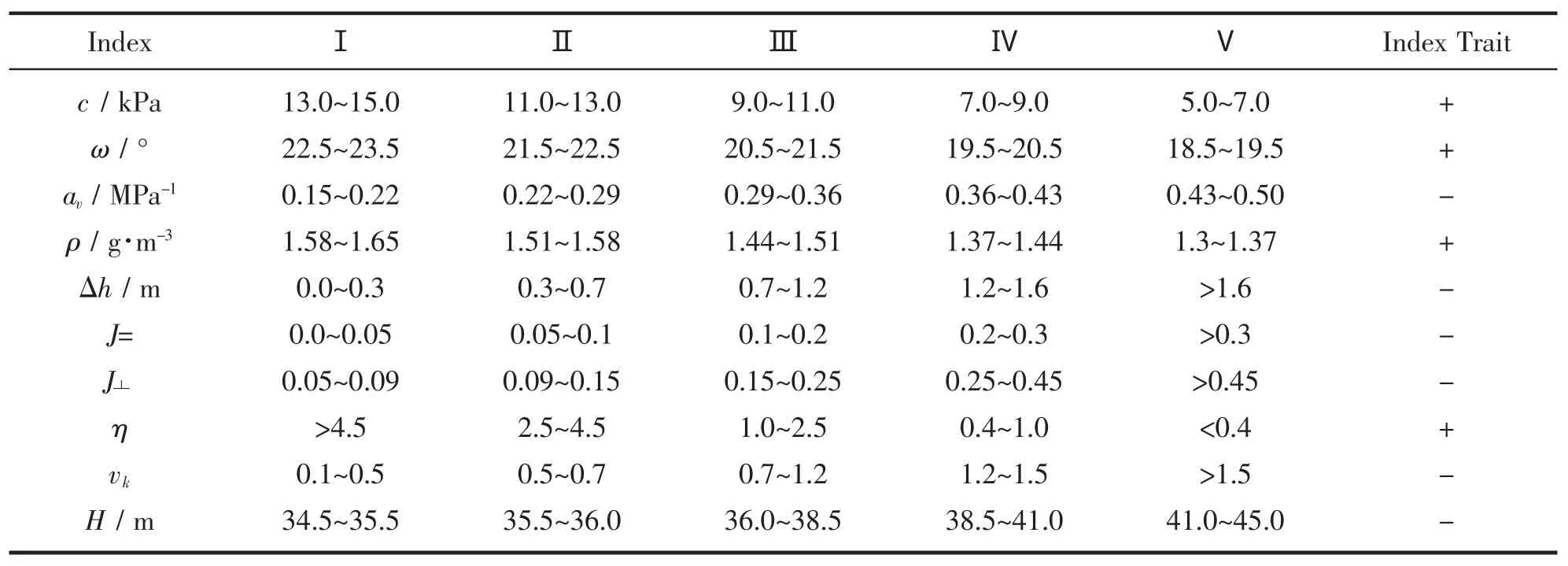
Tab.1 Judgement Grade on Systematic Indexes

To postulate the judgement criterion as the following:Grade I,Grade II,Grade III…D1～D2，D2～D3，D3～D4 …

Then,the corresponding membership function for grade i should be:

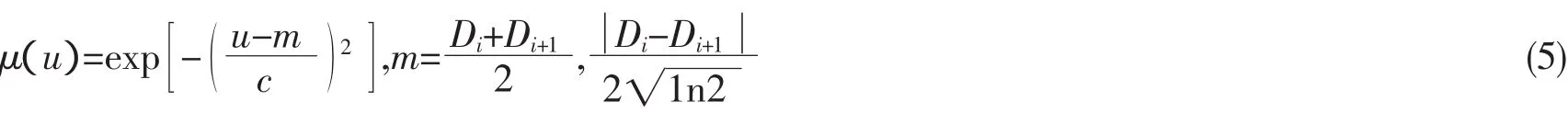
As for the foregoing model systematic indexes,the membership function element rij,under the deterministic fuzzy distribution model,could formulate the membership degree of index i relative to grade j,by which,matrix（ri）jn×m,has constituted the so-called fuzzy correlation matrixthat is mapped from U to V.

3)Weight Vector for Dike Body Safety Model Systematic Indexes

With the reference[13]which has interpreted largely the weight vector formulation and simulation,here,this paper also deduced the initial weight vector of model systematic indexes series by general eigenvector theory and the result could be showed as the following Tab.2.

Furthermore,the paper invited the Weight Vector Inversion Formulation Theory based on Fuzzy Consistency Matrix,by which,the modified weight vector of dike body safety model systematic indexes has been gotten as the Tab.3.

The eventual fuzzy comprehensive judgement implementation should be run with the modified weight vector.

4)Consequence on Fuzzy Comprehensive Judgement of Dike Body Safety Model

With the deterministic normal fuzzy membership function,the comprehensive is carried out respectively for 9 typical dike sections chosen before.The eventual membership grade determination is interpreted by maximal criterion on the degree of membership and the conclusion could be found in Tab.4.

Particularly,the dike body safety model is identified with fuzzy comprehensive judgement theory which could,from the conclusion foregoing,determine the safety-satisfactory level on dike system engineering by the analysis for consistency between the target section and normal section.

3 Generalized Multi-Dimension Weighted Fuzzy Discriminating Model[10]

In order to deepen the insight into the dike body systematic safety characteristics of Yangtse Rive Main Dike in Southern Jingzhou Zone of China,here,based on the foregoing fuzzy comprehensive judgement conclusion,fuzzy model discrimination(or fuzzy model identification)theory should be formulated.

Tab.2 Initial Weight Vector Distribution for AHP Model Systematic Index

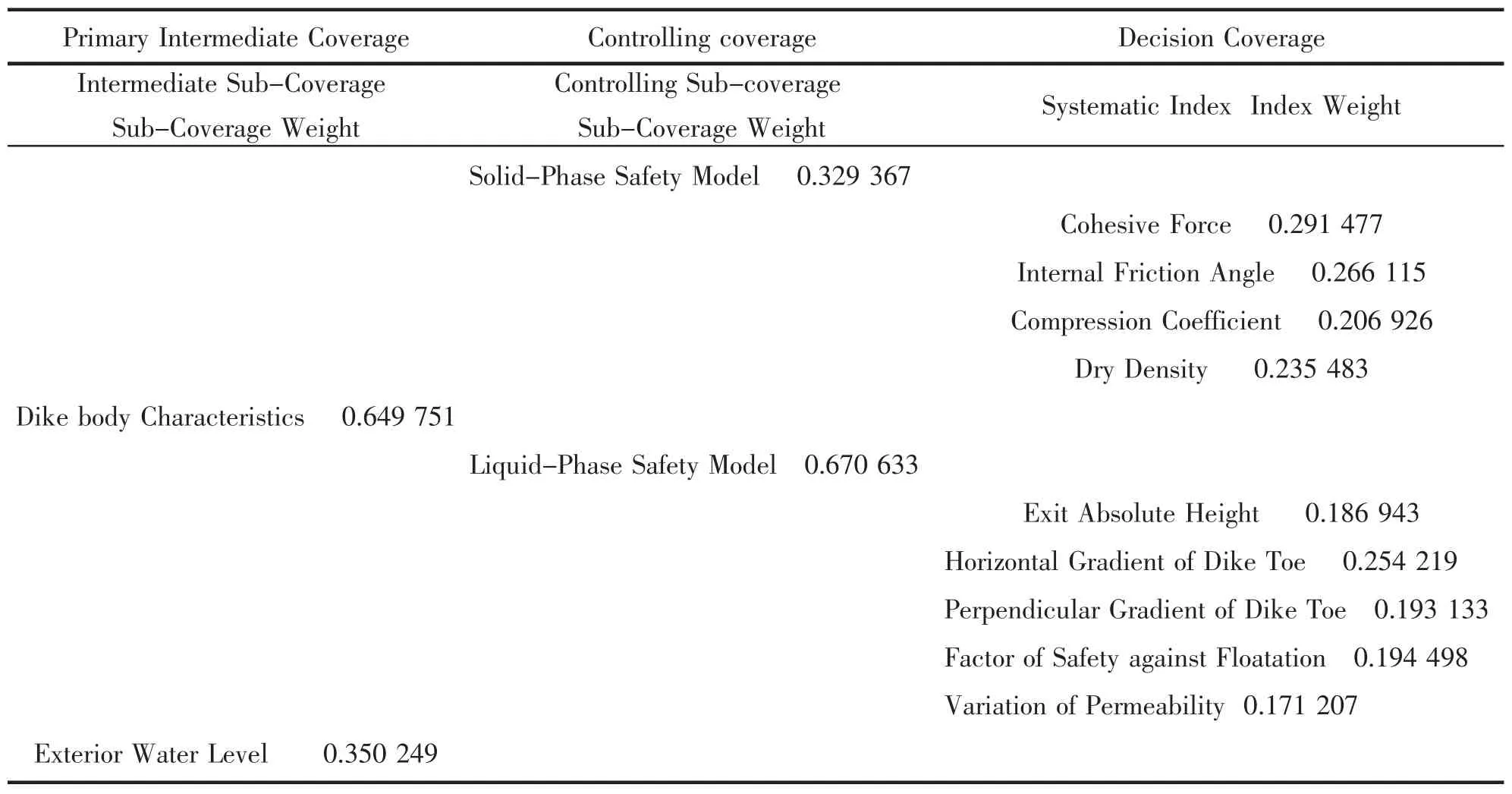
Tab.3 Weight Vector Distribution From Weight Vector Inversion Formulation Theory based on AHP

Tab.4 Safety Grade for Dike Body Section Safety Judgement Model of Yangtse Rive Main Dike in Southern Jingzhou Zone of China

3.1 Immediate Formulation on Fuzzy Model Discrimination

Postulating the group to be identified being U whose sub-group has these indexes series as u1，u2，…up,then,the so-called discrimination sub-group is u=｛u1，u2，… up｝.It is given that there live n categories composing main group U and every category marked withbefore should be a fuzzy sub-group of U.The ultimate function on fuzzy model discrimination,so,is to bracket this sub-group u=｛u1，u2，… up｝into such a category aswhich is the most similar to it.When the membership function being set up,the sub-group u=｛u1， u2，… up｝could be discriminated according to some fuzzy membership criteria that are inclusive of the following:

1)Maximal Membership Grade Criterion

There lives a fuzzy sub-groupon the fuzzy field U where sub-group u1，u2，… upto be identified exist.If μAsub-group uishould be bracketed preferably into this fuzzy sub-group A.

2)Preference Membership criterion

It is given there stand n fuzzy sub-groups(or fuzzy patterns)on the fuzzy field U,namely,A1，A2，…An,and uo∈U is a target to be discriminated.If,sub-group uoshould be bracketed preferably into this fuzzy sub-group

3)Threshold Value Criterion

It is given there stand n fuzzy sub-groups(or fuzzy patterns)on the fuzzy field U,namely,and uo∈U is a target to be discriminated with a deterministic threshold value λ∈[0,1].

Particularly,the immediate formulation on fuzzy model discrimination is applicable to the singular index identification discipline.

3.2 Indirect Formulation on Fuzzy Model Discrimination[11-12]

Different from the foregoing disciplines,when the target model not being the singular element,instead,a fuzzy group on fuzzy field U and the normal model being a fuzzy group on U,too,the indirect formulation on fuzzy model discrimination,then,should be the preferable resort.

It is given that U is the general group on the model to be discriminated and any targetis a fuzzy subgroup on field U in which any element has been donated characteristic indexes series as(u1,u2,…up).With the deterministic fuzzy patterns(or fuzzy sub-groups)on fuzzy field U,the proximitybetweenandhas to be formulated so that the target fuzzy sub-groupto be discriminated could be bracketed into an appropriate fuzzy pattern(i=1,2,…，n),by which,the so-called approximation criterion should be applied to discriminate the category of B.Approximation criterion could be annotated as it that,with fuzzy sub-groupsin addition to fuzzy patternB on fuzzy field U,if σsub-groupshould be bracketed into categoryAi.Here,σ can chosen as any kind of proximity function.The dike safety model discrimination in this paper,so,could be realized by immediate discrimination.

3.3 Generalized Multi-Dimension Weighted Fuzzy Discriminating Model

As a matter of fact,the engineering background is a complicated system which covers a great deal of indexes that may be quantitative or qualitative.The variable weight theory[13],so,should be assimilated here and the multi-dimension proximity fabrication is also formulated in order to install a mature mathematical model which could embody the complex indexes series.

3.3.1 Formulation on General Distance Space

As a primary definition in functional,distance of space,ds(x,y)between x,ymust comply with the following axioms in addition to non-negative characteristics:

1)Non-Negative Characteristics:ds(x,y)≥0,the equation is tenable only when x=y;

2)Symmetry Characteristics:ds(x,y)=ds(x,y)；

3)Triangle inequality:ds(x,y)≤ds(x,z)+ds(z,y)

Distance theory,more often than not,could be adopted in fuzzy discipline to measure the resemblance between two fuzzy groups.Whereas,the General Distance Space is to be defined at first below[14]:Def1:It is given that here exists a indexes group ℓ on the fuzzy fieldand relation between them isFuzzy mapping isand mark ο specifies ideal model with i(i=1,2, …n)specifying model to be identified.,so,could be defined on the fuzzy fieldas General Distance Space.Model group to be discriminated Mn={Md1,Md2,…Mdn}is stipulated consequently.From these hypotheses before,the General Distance could be formulated as:

This function is expressed with tensor representation and the explanation in detail is:

The Variable Weight Space is defined as

Def2:It is given that here exists a indexes group ℓ on the fuzzy fieldand relation between them is

xk∈ℓ being indexes series,i specifying any model to be discriminated(i=1,2,…n),j specifying judgement criterion fuzzy sub-group

Def3:It is given that here exists a indexes group ℓ on the fuzzy fieldand relation between them isFuzzy mapping is.ℓ(D):Dij,then,could be defined to be Multi-Dimension Proximity space,which could be expressed in detail as:

This procedure could be explained as it that General Weighted Distanceis calculated from“controlling coverage”and “intermediate coverage”at first and this process could be called “Multi-Dimension Composition”,furthermore,Multi-Dimension Proximity gotten from“ultimate functional coverage”.

It could be justified that Multi-Dimension Proximity is a proximity function but not the strict proximity function.

Based on the foregoing,General Distance Space could be unfolded as[15][16]

3.3.2 Formulation on Relative Resemblance Space

Def4:It is given that here exists a indexes group ℓ on the fuzzy fieldand relation between them isFuzzymapping isand mark Ο specifies ideal model with i(i=1,2,…n)specifying model to be identi－fied.Model group to be discriminated Mn={Md1,Md2,…Mdn}is stipulated consequently.(Dif):Dif(i,i＇，ο),then,could be definedto be Resemblance Space,spatial group Dif(i,i＇，ο)being Resemblance Degree that specifies the superiority of target i to target i’and formulated as:

The definition of Relative Resemblance Space could be gotten on the basis of Def4 as the following:

Def5:It is given that here exists a indexes group ℓ on the fuzzy fieldand relation between them isFuzzy mapping isand mark ο specifies ideal model with i(i=1,2,…n)specifying model to be identified.Model group to be discriminated Mn={Md1,Md2,…Mdn}is stipulated consequently.(Ref):Ref(ο)i,then,could be defined to be Relative Resemblance Space,which could be annotated as it that how close the model Mdiof Mn={Md1,Md2,…Mdn}is to the ideal model Mdoin terms of the whole group resemblance to be discriminated.The corresponding group Ref(ο)iis Relative Resemblance Grade defined as:

3.3.3 Realization on Model Discrimination

When Relative Resemblance Grade of the whole model group being gotten absolutely,the superior one of them,then,come into being as the ultimate result of the discrimination and could be formulated as

v specifying this model that is the utmost resembling model target as for the ideal model.

The foregoing algorithm could be actualized easily with program SIMPL.for developed in this paper and the flowcharting is showed in Fig.4.

4 Safety Model Discrimination on Typical Dike Body Section of Yangtse Rive Main Dike in Southern Jingzhou Zone of China[16-18]

With the fuzzy comprehensive judgement on systematic model of Typical Dike Body Section of Yangtse Rive Main Dike in Southern Jingzhou Zone of China,furthermore,more meritorious researching case here is to find out which section is much more inclined to fall into such engineering failures as landslide,seepage failure etc that have happened on other cases,which could be bracketed into the category of model discrimination.

4.1 Membership Function Formulation and Normal Model and Discriminating Model Establishment[19]

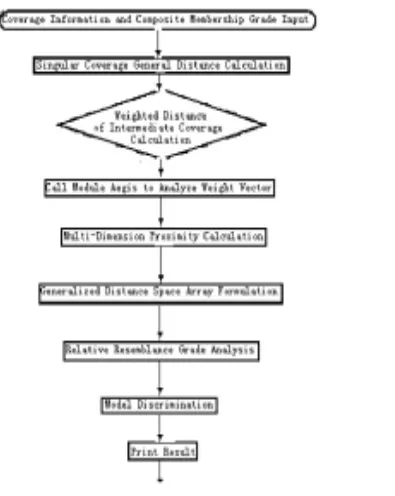
Fig.5 580+500 Section Seepage Field Head Expectation Value Distribution

Dike is filled with porous medium of twain-phase characteristics.Moreover,with the fuzzy stochastic analysis for local dike structure stress field and seepage field (showed as fig1,fig2,fig5,fig6),the normal membership function is the preferable choice for model simulation.With the sound reference,this conclusion could be drawn properly that dike section 630+008JNF has hoarded the utmost safety in 9 typical sections.At the same time,this conclusion could be confirmed by fig.7 that is the eventual conclusion of AHP and FCT comprehensive judgement.Whereas,Section 630+008JNF should be designated as the“Deterministic Superior Model”and other sections are the models to be discriminated.The next step,so,is to find out which model of the 8 sections is the most proximate to section 630+008JNF in terms of safety level.

4.2 Fuzzy Sub-Group of Judgement Criterion

As for the whole discrimination model,the eventual value for any model to be discriminated may be various in view of criterion and the importance of the Criteria is also variable accordingly.The Gross Eigen Vector Theory is applied here to formulateand the conclusion could be found in Tab.5.

4.3 Generalized Distance Space Analysis

With the foregoing deduction,these groups of Generalized Distance Space could be gotten easily as Tab.6.The ideal model Ο=7.

4.4 Relative Resemblance Grade Analysis

With the formulation of Generalized Distancespace,ResemblanceGradeand Relative Resemblance Grade are showed as Tab.7 and Tab.8.The conclusion of Tab.7 proved that,with pairwise comparison of the 8 typical dike body sections,there lives one model that is the most proximate to ideal model 630+008JNF.The conclusion of Tab.8 proved that,with comparison between any model except for the ideal one and the ideal model,the proximity of the former could be gotten to the latter in term of safety level.

From v=6(638+250)，it could be concluded that section 638+250 is the most proximate to ideal model 630+008JNF in terms of dike body model safety characteristics.Factually,with the help of FCT and AHP theory before it has been justified that section 638+250 and section 630+008 are the most proximate couple.As a new theory,model discrimination paved a bridge between the actual engineering disciplines and foregone engineering so that some valuable information could be gotten.In this paper,discrimination twain-phase model of dike body section has been realized with systematic indexes series for which the Multi-Dimension Proximity and Generalized Distance were calculated in order to get the Relative Resemblance Grade by which the proximity between ideal model and sections to be identified could be formulated and this proximity could,in terms of safety characteristics,be implemented according to the approximation criterion annotated before.

4.5 Sensitivity Analysis on Model Systematic Indexes

Just as this paper has annotated before,the fuzzy discrimination model could bridge the correlation between ideal model and models to be identified and find out some valuable information which is inclusive of it that what indexes series have the utmost influence over the model safety characteristics,by which,the local engineering case could be easily researched.This item is the so-called sensitivity analysis on indexes series.

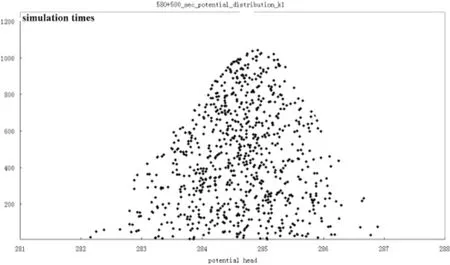
Fig.6 580+500 Section Material Zone 1 Head Scatter Pot

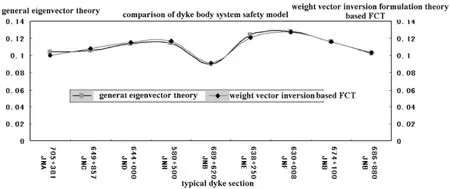
Fig.7 Dyke section system safety model comparison

The sensitivity on fill stuff density,exit absolute height and exterior water level,here,is to be discussed.The density of fill,at first,is postulated 1.6g/cm3and the judgemen result is showed in Tab.9.Secondly,the exit height is postulated to be non-exit and the judgemen result is showed in Tab.10.With the conclusion,it could be gotten that their sensitivity is iota.The fluctuation disturbance of exterior water level,finally,comes into analysis and is postulated 35m of expectation value.The corresponding result shows it that dike body section safety model has obvious reaction very much to this fluctuation.On this basis,the fuzzy threshold value of dike body safety model relative resemblance degree is stipulated 0.99 that is the norm for safety situation.The consequent group contents for“safety model approximation”definition or“normal situation”definition are 4、4、8 respectively in terms of three indexes before,which could be compared with that content of the original situation being 4.The conclusion,then is it that discrimination model here is more sensitive to exterior water level and the result is showed in Tab.11.The judgement criterion group as for the third index can be found in Tab.12.Three sensitivities analyses offered relative resemblance degree contents as Tab.13、14、15.

Tab.5 Fuzzy Sub-group of Judgement Criterion

Tab.6 Generalized Distance

Tab.7 Resemblance Value

Tab.8 Relative Resemblance Value

Ⅰ1 2 3 4 5 6 7 8 Re fi(o) 0.982 325 5 0.993 178 7 0.998 542 4 0.994 976 50.981 327 41.000 000 0.984 893 6 0.982 589 8

Tab.9 Sensitivity Analysis on Systematic Indexes(1)

Tab.10 Sensitivity Analysis on Systematic Indexes(2)

Tab.11 Sensitivity Analysis on Systematic Indexes(3)

Tab.12 Judgement Criterion Group Exterior Water Level Sensitivity Analysis

Tab.13 Relative Resemblance Grade on Fill-Stuff Density Sensitivity Analysis

Tab.14 Relative Resemblance Grade on Exit Absolute Height Sensitivity Analysis

Tab.15 Relative Resemblance Grade on Exterior Water level Sensitivity Analysis

5 Conclusion

1)The Generalized Multi-Dimension Weighted Fuzzy Discriminating Model in this paper could formulate multi-model、multi-index、variable weight in such complex engineering model discrimination case as dike system so that the consequent cognitive model is sound for local engineering background.

2)Model discrimination theory could bridge the correlation between normal engineering case and local engineering cases and the result in this paper consists with fuzzy decision consequent,which,furthermore,justified the practicability of Generalized Multi-Dimension Weighted Fuzzy Discriminating Model on dike boy section safety model discrimination.

3)Safety model discrimination theory could dovetails the deterministic engineering information of normal case and the unidentified information of the model to be discriminated,which is of importance on dike engineering risk judgement system formulation.

4)Generalized Multi-Dimension Weighted Fuzzy Discriminating Mode formulated in this paper could implement the sensitivity analysis on systematic indexes in terms of complicated engineering model system.As for the researching case in this paper,it is identified that exterior water level is the utmost influential factor on dike body safety characteristics.

Acknowledgements

This work was financially supported by Fundamental project fund of Zhejiang Ocean University(Serial number:21045032610)and Initiating project fund for doctors of Zhejiang Ocean University (Serial number:21045011909)

[1]韩宇平,解建仓.模糊综合评判法在水库洪水调度方案评价中的应用[J].西北农林科技大学学报:自然科学版,2002,30(6):198-201.

[2]杨伦标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,1993:213-229.

[3]黄健元.模糊集及其应用[M].银川:宁夏人民教育出版社,1999:127-190.

[4]尉维斌,李珍照.大坝安全模糊综合评判决策方法的研究[J].水电站设计,1996,12(1):1-8.

[5]吴中如,顾冲时,沈振中,等.大坝安全综合分析和评价的理论、方法及其应用[J].水利水电科技进展,1998,18(3):2-6.

[6]彭满华,张海顺,唐祥达.滑坡地质灾害风险分析方法[J].岩土工程技术,2001,15(4):235-240.

[7]徐峻龄.滑坡和崩塌区段预测及稳定度评判的数学地质方法[C]//滑坡文集编委会.滑坡文集:第十三集.北京:中国铁道出版社,1997:5-12.

[8]王亚军.模糊一致理论FCT及层次分析法AHP在荆南干堤典型岸坡段风险综合评价中的嵌套应用[J].浙江水利科技,2004(3):1-3.

[9]刘有志.露天矿山陡边坡稳定性系统分析与评价及其模型的应用研究[D].武汉:武汉理工大学,2002:23-76.

[10]童海鸿,颜国红,詹智民.三峡库区护岸工程堤线优选分析[J].长江科学院院报,2002,19(4):42-44.

[11]王浩,庄则文.模糊可靠性分析中的隶属函数确定[J].电子产品可靠性与环境试验,2000(4):2-7.

[12]李青云.长江堤防工程安全评价的理论和方法研究[D].北京:清华大学,2002.