碳纳米管的振动研究进展

陈彦霖，王晋宝，周 卫，李菲菲，唐志波

（浙江海洋学院船舶与建筑工程学院，浙江舟山 316004）

自从1991年碳纳米管被日本科学家IIJIMA[1]发现以来，已经引起了科学界以及工业界广泛的兴趣。截止目前，已经有大量的研究工作报道了关于碳纳米管的合成、力学、光、电、磁等特性以及其在复合材料中的广泛应用[2-7]。在碳纳米管的广泛应用中，碳纳米管的各种物理特性以及使用功能与其振动特性密切相关。例如：在由碳纳米管形构成的各种微纳机电系统中，纳米管的振动将直接影响着纳米振荡器、电荷探测器、场发射器以及传感器等功效。此外，纳米实验中常常利用碳纳米管的振动来直接或者间接地测量其弹性模量或其他力学行为。因此，碳纳米管的振动特性有广泛的应用前景，开展相关的研究是非常必要的。在过去的10年里，除了开展有限的实验研究工作外，更多的关于碳纳米管的振动研究工作集中于理论数值研究。主要的原因是在纳米层次上进行实验操控是非常困难的，因此推动了理论、数值研究的迅速发展。这些方面的研究主要是基于经典连续体理论模型，以及基于原子模型的分子力学或分子动力学理论等而开展的。本文将针对近年来碳纳米管振动的理论数值研究工作进行详细的综述。

1 经典连续体梁、壳模型

近年来，研究碳纳米管振动采用的连续体模型主要包括经典的欧拉-贝努力梁模型、铁木辛柯梁模型、经典圆柱壳理论以及非局部梁模型等。具体的振动分析包括单、多壁碳纳米管的线性、非线性振动分析。

基于经典的欧拉-贝努力梁模型，YOON等[8-9]发展了用于研究多壁碳纳米管振动的多层欧拉-贝努力连续体梁模型，利用范德华作用描述了多壁碳碳纳米管的层间相互作用，这个多层连续体模型的基本控制方程可表达为

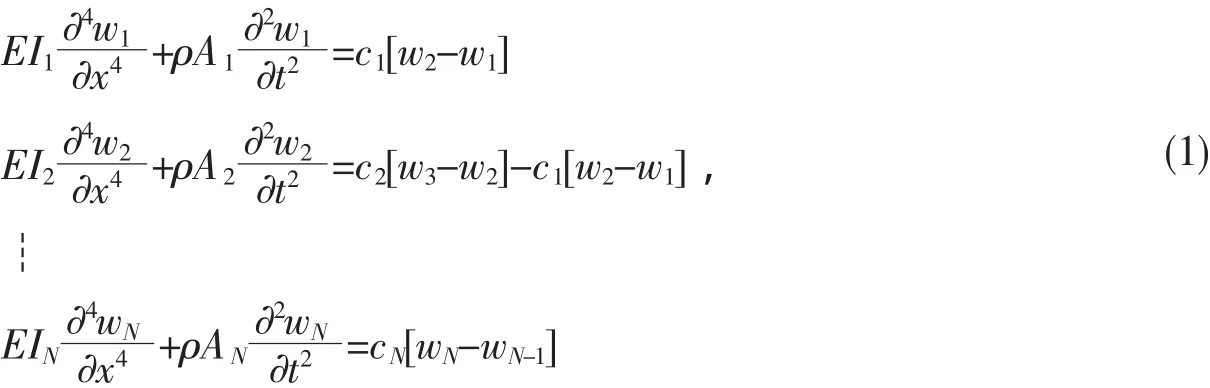
其中，ck为第K层纳米管的范德华作用系数，wk(x,t)第K层纳米管的挠度位移，k=1,2，…，（N-1）。

基于该模型，YOON等[8]预测了多壁碳纳米管的非共轴振动频率以及振动模态，且研究表明非共轴振动将可能发生于较高的自然频率区域。由于非共轴模态的出现，这将明显地影响多壁碳纳米管的基本物理特性。此外，YOON等[9]研究了镶嵌于弹性基体材料中的多壁碳纳米管的振动特性，给出了纳米管的振动频率以及相关的非共轴共振模态，研究表明，当弹性基体材料较刚时，多壁碳纳米管呈现出的均是管间非共轴振动模态；当弹性基体刚度较小时，多壁碳纳米管的振动模态包括整体弯曲和管间非共轴振动模态。基于YOON等[8-9]发展的模型，ZHANG等[10]分析了轴向受压双壁碳纳米管的横向振动特性，分析表明压力的增加将会引起共振频率的减小，但不会改变其内外管的振幅比。值得注意的是，在YOON等[8-9]的研究中，假设多壁碳纳米管的各层均有相同的振动模态。基于假设多壁碳纳米管的各层具有不同的振动模态，NATSUKI等[11]基于同样的多层欧拉-贝努力梁模型研究了双壁碳纳米管在两端简支的情况下的振动特点，模型中同时也考虑了纳米管的层间范德华作用力[12]。研究表明：双壁碳纳米管的振动模态为非共轴的管间振动，且内、外管的位移可能发生同向变化，也可能是反向变化。当半波数相同的情况下，内外管同向振动所对应的双壁碳纳米管的振动频率小于内外管反向振动的频率。在YOON等[8-9]发展的多层连续体梁方程中引入非线性项，FU等[13]研究了以及嵌于基体材料中的双壁碳纳米管非线性自由振动问题。研究表明：弹性基体材料对于纳米管的非线性自由振动有非常明显的影响；当基体材料的刚度较小时，纳米管的非线性自由振动频率随着振幅的增加而快速增加，而当基体材料的刚度足够大时，纳米管的非线性振动趋于线性振动形式。研究还表明，当范德华力较小时，双壁碳纳米管的幅频响应曲线变化剧烈，而当范德华力增大，响应曲线趋于平稳；随着纳米管长细比的增加，双壁纳米管的非线性振动频率将减小。

为了考虑短粗多壁碳纳米管中的剪切变形以及旋转惯性矩的可能的影响，基于经典力学的认知，采用铁木辛柯梁理论比欧拉-贝努力梁理论更为精确。在经典的铁木辛柯梁理论中，由梁弯曲所引起的横向位移和斜率耦合关系为：

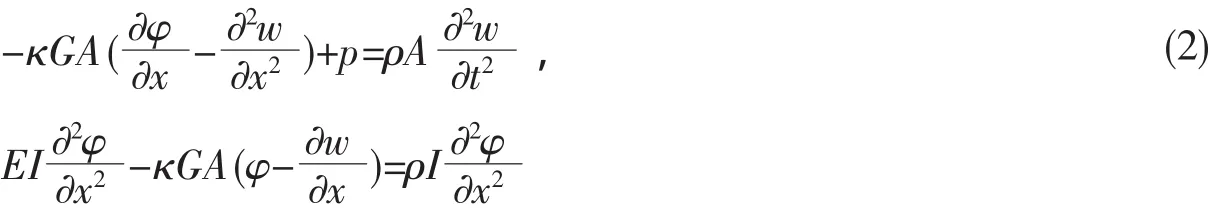
其中κ为剪切因子，与横截面的几何形状相关，p为梁单位长度上的分布荷载。基于上述方程，通过增加反映层间范德华作用的荷载项，YOON等[14]发展了一个双层铁木辛柯梁模型描述了双壁碳纳米管的内、外管的运动，具体研究了长细比分别为10、20和50的双壁碳纳米管的振动特性。研究表明旋转惯性矩和剪切变形对于长细比为10和20的多壁碳纳米管的高频振动短梁的高频振动。基于铁木辛柯梁以及冯卡门几何非线性关系，KE等[15]研究了由单壁碳纳米管增强的功能梯度复合材料的非线性自由振动特征，同时讨论了体分比、振幅、长细比以及端部约束条件对复合梁的非线性自由振动的影响。

近年来，基于非局部欧拉梁、非局部铁木辛柯梁模型以及高阶梁模型，KIANI[16]对比地研究了镶嵌于弹性基体材料中的单壁碳纳米管在不同的边界条件下的自由振动行为，主要分析了纳米管的长细比、初始轴向力以及集体材料的刚度对梁振动频率的影响。基于冯卡门几何非线性梁以及非局部理论，YANG等[17]研究了非局部尺度参数对单壁碳纳米管的非线性自由振动的影响，研究结果表明：对于给定的振动幅值，非局部尺度参数的增大将导致较小的线性和非线性频率之比；随着单壁碳纳米管的长度增加以及半径减小时，线性与非线性频率之比将减小；非局部尺度参数对于非线性模态有着非常明显的影响。

除了基于梁模型的研究，近年来也涌现出一些利用壳模型研究单、多壁碳纳米管的线性、非线性振动的工作。WANG等[18]也对比性地研究了基于Donell壳和Flugge壳方程研究单壁碳纳米管振动和屈曲等的适用性和局限性。研究表明：两个壳模型可以很好地预测单壁碳纳米管的径向呼吸模态，并取得与分子动力学较为一致的结果。对于更广泛的碳纳米管问题而言，基于Flugge壳模型更精确一些。继而，考虑管间范德华力的作用，WANG等[19]基于Flugge弹性壳理论发展了一个多层弹性壳模型，并分别研究了内层半径为5 nm和0.65 nm的多壁碳纳米管的振动特性。通过这个壳模型，不仅描述了纳米管的径向呼吸模态，同时也描述了整体的弯曲模态。研究表明范德华作用对于较大管径（半径为5 nm）的呼吸振动模态有很明显的影响；而对于较小管径（半径为0.65 nm）的纳米管影响较小，特别是对于扭转和轴向模态影响几乎是可以忽略的。WANG等[19]把这一现象归因于控制方程中仅依赖于径向位移变化，而与管径不相关的范德华力模型的使用。MAHAN[20]利用经典的各项同性薄壳弹性解研究了单壁碳纳米管的低频以及弯曲、扭转、径向呼吸和轴向模态。QU等[21]基于非线性Donell壳模型以及HE等[12]发展的可以描述多层碳纳米管间相互作用的范德华模型研究了多壁碳纳米管的内管半径、层数、管长、半波数以及层间范德华力对于其非线性振动行为的影响，其中范德华作用尤为重要。基于哈密顿原理，KUANG等[22]给出了考虑几何非线性以及非线性范德华作用力的传输液体的双壁碳纳米管的振动控制方程，继而分析了非线性因素以及流速等对系统振动频率的影响。类似地，YAN等[23]利用Donnell圆柱壳以及势流理论研究了传输流体的多壁碳纳米管的自由振动问题。研究表明：由于流体的影响，多壁碳纳米管的振动频率减小，且系统呈现的是非共轴振动模态。此外，SHI等[24]利用经典的圆柱壳理论以及有限元理论研究了单壁碳纳米管的振动模态以及不同模态转换的机理。研究表明纳米管的等效厚度对于模态的转换有很重要的影响，且不同的管的厚度可能引发不同频率的内振（即2:1以及1:1）。

2 分子结构力学以及原子有限元模型

在前述工作中，碳纳米管通常被模拟为质量连续分布的连续体来研究，但是碳纳米管的原子微结构信息常常被忽略。通过有效地结合原子微结构信息，LI和CHOU[25-27]基于分子力学发展了分子结构力学模型，LIU等[28]基于描述碳原子间相互作用的原子势能发展了原子有限元模型，这些模型均较好地再现了碳纳米管的微结构信息，同时有效地利用了宏观的求解手段。

分子结构力学模型首先是由LI和CHOU[25]提出用来研究碳纳米管的相关力学特性。其基本思想源于微观纳米管和宏观框架结构的相似性，即模拟碳纳米管为类框架结构，其中碳原子间的共价键被模拟为无质量的梁单元，碳原子模拟为集中质量的单元节点。通过能量等价的原理，建立分子力学局部原子势和计算结构力学单元应变能之间的等价关系，从而确定出结构分析所需要的等价梁单元的抗张拉、抗弯曲和抗扭转刚度，即

其中L是晶键长度，EA，EI，GJ分别是梁单元的抗拉、抗弯和抗剪切刚度，kr、kθ和kτ分别是晶键在拉伸、弯曲和扭转作用下所对应的分子力场参数。这些力场参数来自于石墨片的实验结果，分别为kr/2=469 kcalmol-1A-2，kθ/2=63 kcalmol-1rad-2和 kτ/2=20 kcalmol-1rad-2。由此，根据式（3）可以确定等价碳碳晶键的梁单元的抗拉、抗弯及抗扭刚度，进一步，针对所研究的碳纳米管结构模型建立组装系统的总刚度阵和总质量阵，最终通过经典的结构力学方法求解碳纳米管的静、动力学问题。基于此，LI和CHOU[26-27]围绕碳纳米管开展了大量的静、动力学问题研究。通过建立如下的运动学方程，他们研究了碳纳米管的自由振动特性

其中M为系统总质量阵，K为系统总刚度阵，y和ÿ分别为节点位移和加速度。假定该振动为谐波振动，最终简化求解由方程（4）所得问题的特征值和特征矢量，即可获得碳纳米管的自由振动频率和振动模态。

基于分子结构力学，LI和CHOU[26]首先预测了悬臂单壁碳纳米管的振动频率可以达到10 GHz～1.5 THz，并研究了纳米管的直径、长度以及端部约束对于基频的影响；继而，研究了双壁碳纳米管的振动特性[27]，研究表明双壁碳纳米管的基频比相同外管径的单壁碳纳米管的基频低10%，且管间非共轴振动模态出现于第三阶振动频率处。进一步，CHEN[29]修正了LI和CHOU[25-27]的分子结构力学，调整了原模型中表征原子晶键的等效弯曲刚度，同时在模型中加入了温度的描述，因此这一模型也被称为修正分子结构力学。基于该模型，CHENG[30]研究组研究了单、双壁碳纳米管的径向呼吸模态以及类径向呼吸模态，以及纳米管管径、长细比、层数、手性和温度对振动频率的影响。研究表明：对于小直径的纳米管，径向呼吸模态对于管径和手性是敏感的且成反比；当外半径相同时，双壁碳纳米管的径向呼吸模态频率比单壁碳纳米管的相应模态频率大，且对于锯齿形大2%～8%，对于扶手型大6%～10%；不管纳米管的层数多少，锯齿型碳纳米管的径向呼吸模型频率总大于扶手型相应的频率；锯齿型碳纳米管的径向呼吸模态频率随着管长细比的增加和轻微地减小，且当长细比大于1.25时，标准的径向呼吸模态将转换成类径向呼吸模态；随着温度的增加，纳米管的原子晶键键长增加，而相关的键角减小，因此，当温度从300 K增加到2 000 K时，锯齿型和扶手型纳米管的径向呼吸模态频率将减小2%。类似地，通过线性弹簧-集中质量模型，即模拟碳-碳键为线性弹簧，碳原子为集中质量粒子，GEORGANTZINOS等[31]研究了多壁碳纳米管的振动模态。结合分子力学中能够合理描述碳原子间延伸、弯曲、扭转等原子势能以及谐函数表达形式，作者分别确定出线性弹簧模型的拉伸刚度、弯曲刚度以及扭转刚度，继而通过经典结构力学中集中质量-弹簧模型的计算方法研究了简支边界条件下多壁碳纳米管振动问题。研究表明，纳米管的层数以及长细比对于纳米管的基频有着非常明显的影响。

原子有限元方法是由LIU等[28]提出的，其突出的优点是基于有限元框架实现了原子和连续体域的无缝连接，避免了人工界面的产生，保证了计算精度和准确度。主要的思想是对整个研究系统的所有原子位移进行系统能量最小化，采用类似于有限元的基本思想，对能量最小化后所得的所有方程进行综合集成，表达为

其中刚度矩阵，不平衡力是第i 个原子的位置矢量，Etot是系统的总能，包含了系统原子势能以及外力势能，Fi是作用于第i个原子上的外力。利用上述模型中的刚度矩阵以及纳米管系统中原子的质量阵可以分析单壁碳纳米管的振动特性。LIU等[28]研究了由400个碳原子组成的、端部为悬臂约束的(5,5)扶手型单壁碳纳米管振动频率和模态，前三阶振动频率分别为112、614和685 GHz，且前两阶模态类似于经典的悬臂梁模态，第三阶模态为径向呼吸模态。进一步，SHI等[32]基于原子有限元研究了单、多层碳纳米环间的振动模态转换机理，研究表明单层纳米碳环（分别由10～60个原子）中可激发2:1的内振；当高速径向呼吸模态开始施加于碳环时，径向呼吸振动一个周期后，可以观察到环向弯曲振动模态被激发，之后可以观察到径向呼吸模态和环向弯曲模态的不断的模态转换过程；对于多层碳环而言，由于环间的作用力，2:1的内振形式可能转换为1:1的内振形式。

3 原子模拟

分析碳纳米管振动的原子模拟方法主要包括经典分子动力学、从头分子计算以及紧束缚分子动力学等。基于原子模拟的研究，可以全面地反映纳米管手性微结构和半径的影响因素，但是这些方法最大的不足在于计算量大、耗时，且仅局限于原子规模较小的计算系统。因此，基于该类方法的纳米管振动研究工作相比连续体理论的研究较少。

利用从头分子计算以及赝势密度泛函理论，SANCHEZ-PORTAL等[33]研究不同管径和手性的单壁碳纳米管的结构、弹性以及振动特性。研究结果表明纳米管的径向呼吸模态对应的频率与管的直径和手性相关。基于分子动力学，ZHOU和SHI[34]也研究了施加于单壁碳纳米管上的张拉荷载引起的径向自激励振动，振动频率为4 700 GHz，且振动频率与张拉率无关。基于并行紧束缚分子动力学，DERELI和OZDOGAN[35]研究了轴向张拉由400个原子组成的（10,10）扶手型碳纳米管的基本力学特性。同时发现了一个有趣的现象，即轴向加载诱导的径向振动，其振动频率为4.71 THz。研究也发现径向振动频率是与轴向应变是密切相关的，即增加纳米管结构的应变将导致径向振动频率的减小。

4 结论

由于碳纳米管近年来的广泛工业应用，如基于碳纳米管的传感器、分子马达、高频振荡器的微纳米器件的不断问世，引起了近5年来碳纳米管振动力学行为的理论研究的迅速提升，包括从经典的连续体模型到原子尺度的分子动力学，甚至量子力学研究手段的应用。然而，连续体模型无法再现碳纳米管的手性等微结构特性；基于原子尺度的分子、量子力学手段受限于研究系统的空间、时间尺度，尽管基于分子结构力学以及原子有限元可以较好的解决前述不足，但是事实上当这两类方法应用于多壁碳纳米管等的复杂系统，仍然面临着计算规模的剧增所引起的巨大计算代价的付出，主要是由于这两类方法跟踪的仍是原子结构。因此，为了更全面地了解碳纳米管的振动特性，为其工程应用提供客观全面的理论依据，更深入的理论研究以及实验研究仍然是迫切需要的。

[1]IIJIMA S.Helical microtubules of graphitic carbon[J].Nature,1991,354:56-58.

[2]THOSTENSON E T,REN Z,CHOU T W.Advances in the science and technology of carbon nanotubes and their composites:a review[J].Composite Science and Technology,2001,61(13):1 899-1 912.

[3]QIAN D,WAGNER J G,LIU W K,et al.Mechanics of carbon nanotubes[J].Applied Mechanics Review,2002,55(6):495-533.

[4]LIU J,FAN S S,DAI H J.Recent advances in methods of forming carbon nanotubes[J].MRS Bull,2004,29(4):244-250.

[5]BAUGHMAN R H,ZAKHIDOV A A,DE HEER W A.Carbon nanotubes-the route toward applications[J].Science,2002,297:787-792.

[6]CHOI W B,BAE E,KANG D,et al.Aligned carbon nanotubes for nanoelectronics[J].Nanotechnology,2004,15:512-516.

[7]GIBSON R F,AYORINDE E O,WEN Y F.Vibrations of carbon nanotubes and their composites:a review[J].Composites Science and Technology,2007,67(1):1-28.

[8]YOON J,RU C Q,MIODUCHOWSKI A.Noncoaxial resonance of an isolated multiwall carbon nanotube[J].Physical Review B,2002,66(23):2 334 021-2 334 024.

[9]YOON J,RU C Q,MIODUCHOWSKI A.Vibration of an embedded multiwall carbon nanotube[J].Composites Science and Technology,2003,63(11):1 533-1 542.

[10]ZHANG Y,LIU G,HAN X.Transverse vibrations of double-walled carbon nanotubes under compressive axial load[J].Physical Letter A,2005,340:258-266.

[11]NATSUKI T,NI Q Q,ENDO M.Analysis of the vibration characteristics of double-walled carbon nanotubes[J].Carbon,2008,46:1 570-1 573.

[12]HE X Q,KITIPORNCHAI S,WANG C M,et al.Modeling of van derWaals force for infinitesimal deformation of multi-walled carbon nanotubes treated as cylindrical shells[J].International Journal of Solids and Structure,2005,42(23):6 032-6 047.

[13]FU Y M,HONG J W,WANG X Q.Analysis of nonlinear vibration for embedded carbon nanotubes[J].Journal of Sound and Vibration,2006,296:746-756.

[14]YOON J,RU C Q,MIODUCHOWSKI A.Terahertz vibration of short carbon nanotubes modeled as Timoshenko beams[J].Journal of Applied Mechanics,2005,72(1):10-17.

[15]KE L L,YANG J,KITIPORNCHAI S.Nonlinear free vibration of functionally graded carbon nanotube-reinforced composite beams[J].Composite Structures,2010,92:676-683.

[16]KIANI K.A meshless approach for free transverse vibration of embedded single-walled nanotubes with arbitrary boundary conditions accounting for nonlocal effect[J].International Journal of Mechanical Sciences,2010,52:1 343-1 356.

[17]YANG J,KE L L,KITIPORNCHAI S.Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory[J].Physica E,2010,42:1 727-1 735.

[18]WANG C Y,RU C Q,MIODUCHOWSKI A.Free vibration of multiwall nanotubes[J].Journal of Applied Physics,2005,97:114 323.

[19]WANG C Y,RU C,MIODUCHOWSKI A.Applicability and limitations of simplified elastic shell equations for carbon nanotubes[J].Journal of Applied Mechanics,2004,71:622-631.

[20]MAHAN G D.Oscillations of a thin hollow cylinder:carbon nanotubes[J].Physical Review B,2002,65:235402.

[21]QU C Y,HE X Q,QIN Q H.Nonlinear Vibration of Multi-walled Carbon Nanotubes[C].Proceedings of the World Congress on Engineering,London,UK,2007.

[22]KUANG Y D,HE X Q,CHEN C Y,et al.Q.Analysis of nonlinear vibrations of double-walled carbon nanotubes conveying fluid[J].Computational Materials Science,2009,45:875-880.

[23]YAN Y,WANG W Q,ZHANG L X.Noncoaxial vibration of fluid multi-walled carbon nanotubes[J].Applied Mathematical Modelling,2010,34:122-128.

[24]SHI M X,LI Q M.Mode transformation in single-walled carbon nanotubes[J].International Journal of Mechanical Sciences,2010,52:663-671.

[25]LI C,CHOU T W.A structural mechanics approach for the analysis of carbon nanotubes[J].International Journal of Solids and Structures,2003,40:2 487-2 499.

[26]LI C,CHOU T W.Single-walled nanotubes as ultrahigh frequency nanomechanical resonators[J].Physical Review B,2003,68:073405.

[27]LI C,CHOU T W.Vibrational behaviors of multiwalled-carbonnanotube-based nanomechanical resonators[J].Applied Physics Letters,2004,84(1):121-123.

[28]LIU B,HUANG J Y H,QU S,et al.The atomic-scale finite element method[J].Computer Methods in Applied Mechanics and Engineering,2004,193:1 849-1 864.

[29]CHEN W H,CHENG H C,LIU Y L.Radial mechanical properties of single-walled carbon nanotubes using modified molecular structure mechanics[J].Computational Materials and Sciences,2010,47:985-993.

[30]CHENG H C,LIU Y L,WU C H,et al.On radial breathing vibration of carbon nanotubes[J].Computer methods applied mechanics and engineering,2010,199:2 820-2 827.

[31]GEORGANTZINOS S K,ANIFANTIS N K.Vibration analysis of multi-walled carbon nanotubes using a spring-mass based finite element model[J].Computational Materials Science,2009,47:168-177.

[32]SHI M X,LI Q M,LIU B,et al.Atomic-scale finite element analysis of vibration mode transformation in carbon nanorings and single-walled carbon nanotubes[J].International Journal of Solids and Structures,2009,46:4 342-4 360.

[33]SANCHEZ-PORTAL D,ARTACHO E,JSOLER J M.Ab initio structural,elastic and vibrational properties of carbon nanotubes[J].Physical Review B,1999,59(19):12 678-12 688.

[34]ZHOU L G,SHI S Q.Molecular dynamics simulations on tensile mechanical properties of single-walled carbon nanotubes with and without hydrogen storage[J].Computational Materials and Science,2002,23:166-174.

[35]DERELI G,OZDOGAN C.Structural stability and energetics of singlewalled carbon nanotubes under uniaxial strain[J].Physical Review B,2003,67(3):035416.