一种混沌序列加密算法的密码分析

蔡 琼，彭 涛，叶 杨

(武汉工程大学 计算机科学与工程学院，湖北 武汉 430074)

1 混沌序列加密算法

由于混沌映射所具有的许多类似随机的性质和密码学中的混淆和扩散等性质相似，所以出现了很多混沌加密算法，本文分析的混沌序列密码算法使用的是Logistic[1]映射.

f(x)=μx(1-x),x∈[0,1],μ∈[3.5699456,4]

(1)

当x∈[0,1],μ∈[3.5699456,4]时，Logistic映射具有混沌效应.然而由于实数在计算机中以有限的精度实现，对于每次迭代产生的x可以表示如下：

其中n表示精度.

明文分组长度是64 bit,密钥是混沌的初始控制参数x0和μ.该加密算法如下四步：

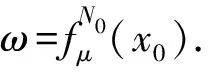
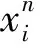
其中Aj为64bit分组，Dj为小于64的整数.

c. 加密明文分组，明文分组Mj对应的密文分组Cj=(Mj≪Dj)⊕Aj.然后把密文块做一个映射，φ(Cj)=cj+cj+1+…+cj+7,D*=Dj+φ(Cj)mod64.

d. 如果所有的明文分组都被加密则加密结束，否则ω=fD*+70(ω)，然后转到b继续加密.

2 加密系统的信息泄露规律以及攻击

虽然文献[2]对该加密系统进行了改进，但文献[3]指出了该加密算法对密钥的分割攻击存在安全隐患.加密算法步骤a实质上是为了掩盖混沌初态，来增加系统的安全性，但是如果以迭代之后的ω为初态，以参数μ产生的混沌序列，与以x0为初态经过迭代之后产生的混沌序列是一致的.这样就可以把ω视为x0的等效密钥，只要完成了对{ω,μ}的攻击就完成了对加密系统的攻击.

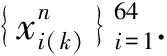
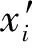
定理2[5]设函数f(x)=μx(1-x),μ,μ+δ∈(3.5699456,4],x,x+ε∈[0,1]，则:

证明：由于函数f(x)在[0,1]是连续可导的，则由拉格朗日中值定理知，存在

ξμ∈[x,x+ε],ηx+δ∈[μ,μ+δ]

使得

(2)

(3)

将(2)、(3)两式相加得到

|fμ(x)-fμ+δ(x+ε)|=

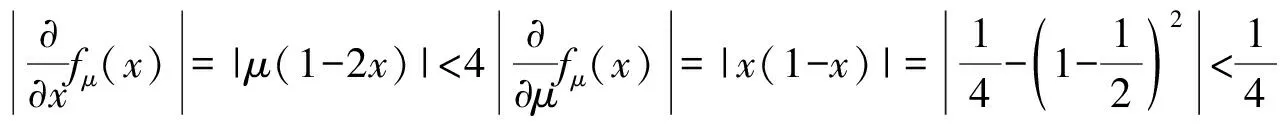
定理1、2说明，Logistic混沌映射具有如下性质：输入的低位变化对输出的高位影响不大，而上述加密系统中的实际用来加密的二进制流，是由混沌映射反复迭代产生的，这就导致了混沌序列具有前几个值对混沌初态和参数的低位比特变化不够敏感的性质；由随机序列的产生方式知，当输入发生轻微变化时，输出几乎不变.从为了定量刻画这种性质，引入吻合度的概念.

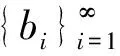
将{ωn,μn}的吻合度记为tn,要从理论上精确分析tn的分布规律是困难的.文献[4]用模拟分析方法给出了密钥为64 bit，算法的吻合度分布的统计规律.

表1 T16的分布规律

一般地有:p(t8≥9)=0.992 4,p(t16≥9)=0.990 2,p(t24≥9)=0.989 3,p(t32≥29)=0.980 0,p(t40≥37)=0.988 3,p(t48≥46)=0.986 0.

设{ω,μ}为正确的密钥，若同时穷举密钥中两个数的高nbit，则tn≥t吻合度的试验密钥的个数期望为22n-1,且吻合度tn≥t的试验密钥中包含{ωn,μn}的概率为p(tn≥t).当试验密钥{ω′n,μ′n}与{ωn,μn}不相等时，可认为由{ω′n,μ′n}产生的的序列与乱数序列相互独立，因而{ω′n,μ′n}产生的序列的吻合度tn≥t的概率近似为2-t,而由模拟试验知，{ωn,μn}的吻合度tn≥t的概率相对于2-t要大得多.据此就可将随机试验密钥{ω′n,μ′n}和{ωn,μn}区分开.由上述模拟实验结果可知，利用已知明文采取先攻击高位密钥再攻击低位密钥的方法对这两个密码算法进行分割攻击，即依次攻击k8,k16,k24,k32,k40,k48，每次选取前者的候选密钥，可最终获得正确密钥，而不漏掉正确密钥的概率为:

p=p(t8≥1)p(t16≥9)p(t24≥19)p(t32≥29)p(t40≥37)p(t48≥46)=0.92 4×0.990 2×0.989 3×0.980 0×0.988 3×0.986 0≈0.928 4

即该加密系统是不安全可破的.

3 改进办法

针对上述问题，若要确保吻合度分布的合理性才能避免上述分割攻击，需引入比特矩阵.由于随机序列任然具有前几个比特对混沌初态和参数的低位比特变化不够敏感的性质，所以改变随机序列[6]的产生方式.

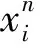
M10×10=

如果上式将100位比特串划分为Aj1、Aj2、Aj3.其中将Aj2表示为对64取模的整数Dj.

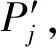
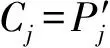
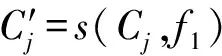
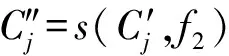
其中，s(c,n)表示把c循环左移n位.

如果所有的明文块加密完毕则结束，否则执行下述操作，然后转至步骤(b).

D*=Dj+f(Cj″)mod64

ω=fD*+70(ω)

4 改进后的安全性分析

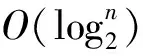
由于矩阵乘法具有结合律，如A4=A2·A2,因此有如下结论：当n为偶数时，An=A(n/2)·A(n/2)；当n为奇数时，An=A(n/2)·A(n/2)·A，(n/2取整)，依次递归计算，并在计算过程中不断对2取模，避免高精度运算.

4.1 初值敏感性分析

对混沌系统的初始条件进行微小变化，通过统计产生的二值序列中相应位置上的1和0的值的变化情况，计算相应的序列位变化率.位变化率的定义如下：

其中n为序列长度，n′为初始条件进行微小改变后生成的二值序列与原序列比较，相应位变化的个数.取μ=3.659 6，比较随机序列的前70位得到的结果表2所示.

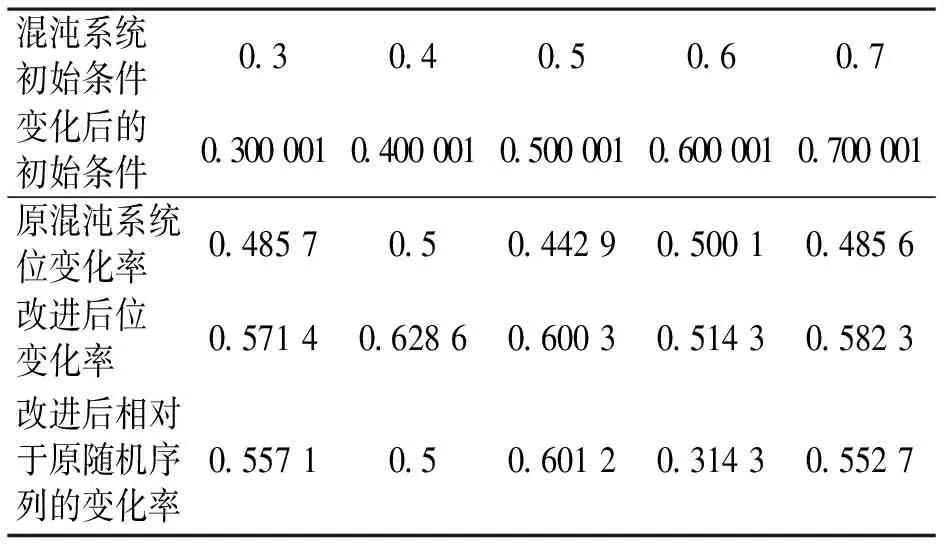
表2 序列变化率

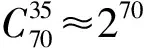
4.2 密钥吻合度分析

取μ=3.659 6，密钥为64 bit，随机选取10 000个密钥统计得到如图1～4所示的吻合度分布图，其中虚曲线代表改进之后的吻合度分布，实线代表之前的吻合度分布.改进之后的吻合度分布趋向于随机化，即p(tm≥t趋向于2-t,故改进之后使得基于密钥的分割攻击变得无效.

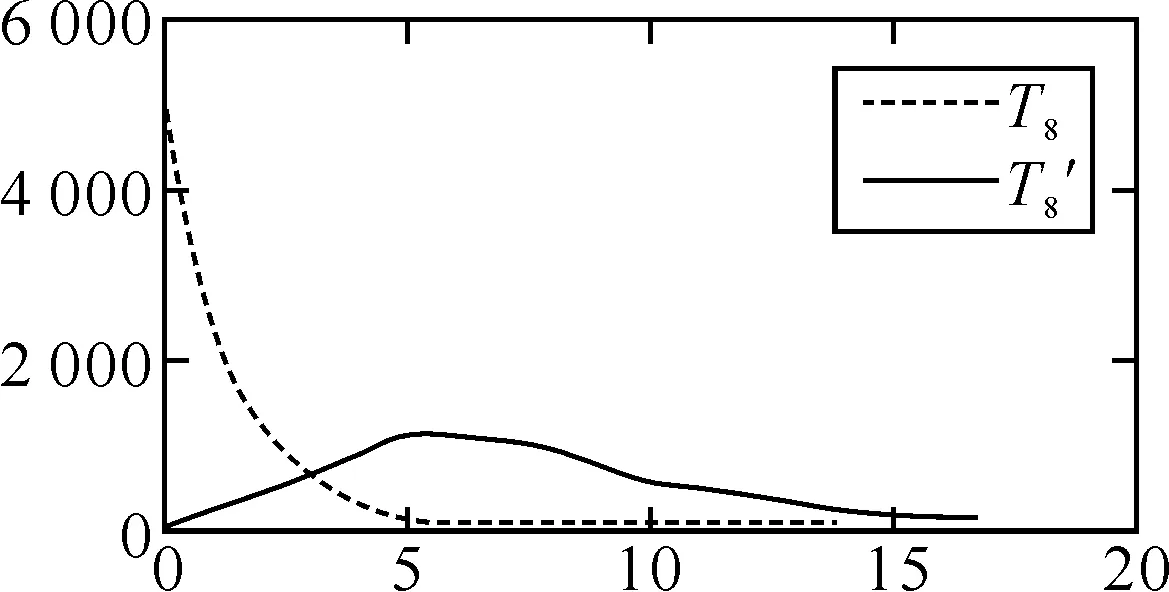
图1 T8的分布规律

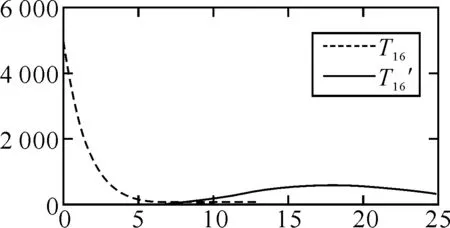
图2 T16的分布规律

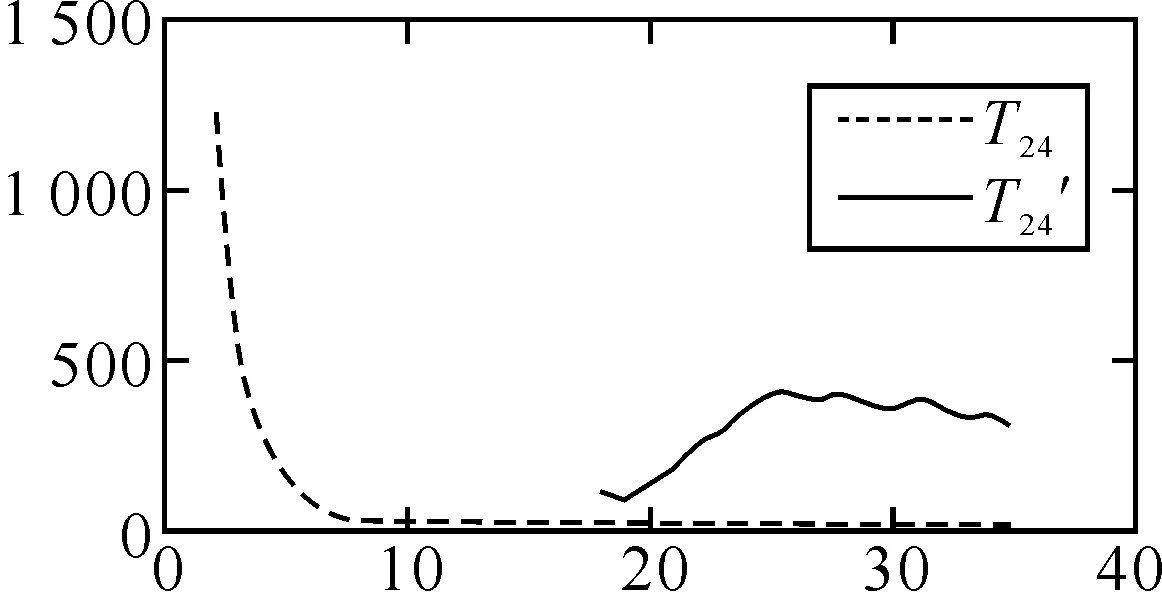
图3 T24的分布规律

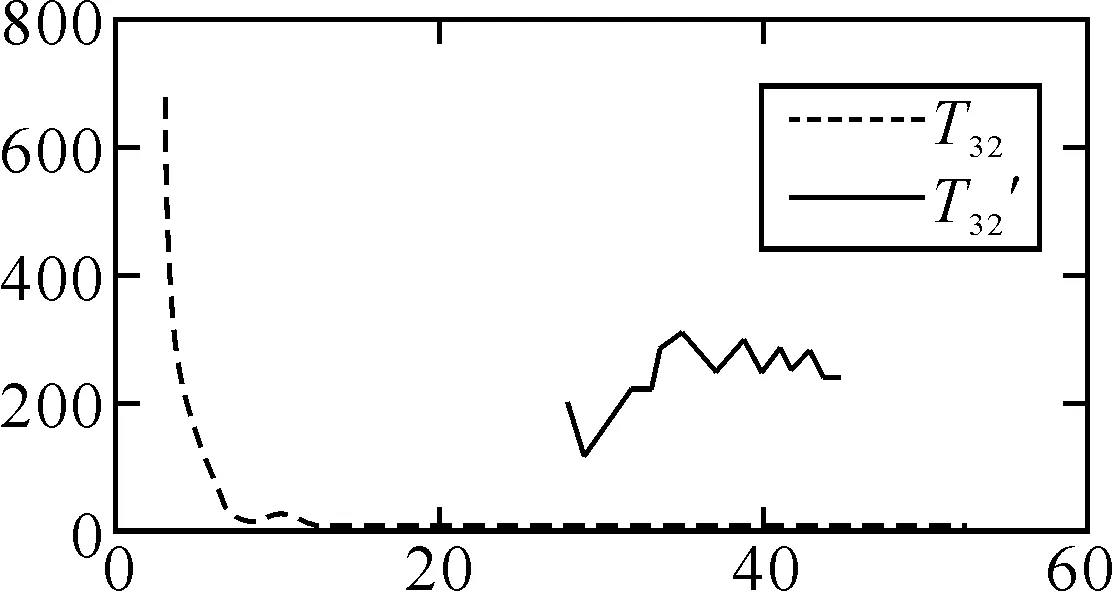
图4 T32的分布规律

4.3 对于选择明文攻击

假设Pz与明文块长度相同(64位),且全为0，相应的密文为Cz，则有下式(a);假设Ps与明文块长度相同(64位),且第一位为0，其他全为1,相应的密文为Cs,则有

s(s(s(Pz,Dj)⊕Aj1,f1)⊕Aj3,f2)⊕Aj1=Czs

(s(Aj1,f1)⊕Aj3,f2)⊕Aj1=Cz

(4)

s(s(s(Ps,Dj)⊕Aj1,f1)⊕Aj3,f2)⊕Aj1=Cs

(5)

由式(4)和式(5)无法推导出Aj1,Aj3,穷举264·264·64·64=2140次方可列举全部的组合.

5 结 语

针对一个基于混沌设计的分组密码算法所产生的混沌序列具有前几个值对混沌初态的低位比特变化不敏感，无法抵抗在选择明文攻击条件下对密钥的分割攻击，提出了增加矩阵取模幂乘运算，并改进算法中参数的控制，由密钥吻合度分布实验可知，可基本确保任意两个不同的试验密钥产生的乱数序列相互独立，并且对初始值的变化有更好的敏感性，使得改进之后的算法，能抵抗对密钥的分割攻击和选择明文攻击.

参考文献：

[1] Xiang T,Liao X F,Tang G P, et al. A novel block cryptosystem based on iterating a chaotic map[J].Physics Letters A,2006(349):109-115.

[2] Wang King-yuan,Yu Cang hai.Cryptanalysis and improvement on a cryptosystem based on a chaotic map

[J]. Computers and Mathematics with Applications,2009(57):476-482．

[3] 张涛.一个混沌分组密码算法的分析[J].计算机应用研究,2010,27(6)：2294-2296.

[4] 金晨辉.一个基于混沌的分组密码算法的分析[J].中国工程科学，2001,3(6):75-80.

[5] 金晨辉，高海英．对两个基于混沌的序列密码算法的分析[J]．电子学报，2004，32(7)：1066-1070．

[6] 杨建华.数列组的广义线性相关性[J].武汉工程大学学报,2009,31(12)：79-81.

[7] 胡端平，唐超.一致矩阵的特征性质[J].武汉工程大学学报，2009，31(5)：93-94.